南苏丹P区块高孔隙度高渗透率储层束缚水饱和度确定方法

马小林,陈科贵,黄亮,李冰,郭红光,蒋新宇

(1.西南石油大学地球科学与技术学院,四川成都610500;2.中国石油集团测井有限公司国际事业部,北京100000;3.中国石油集团测井有限公司长庆分公司,陕西西安710000)

0 引 言

一直以来,束缚水饱和度都是储层评价的难题,虽然其在储层评价中有重要作用,但是没有一种能独立评价束缚水饱和度的解释模型。前人对束缚水饱和度模型建立已经开展了很多研究,雍世和等[1]根据中国东部6个油田的取心分析资料,采用数学统计分析方法建立了束缚水饱和度的经验公式;陈科贵等[2]通过核磁共振测井资料,利用孔隙度指数建立束缚水饱和度模型;朱林奇等[3]利用核磁共振测井资料结合压汞实验预测束缚水饱和度模型。

南苏丹P区块缺乏密闭取心资料以及核磁共振测井资料,该区高孔隙度高渗透率储层建立束缚水饱和度模型存在很大的难度,本文基于研究区5口取心井的岩心分析资料,通过对束缚水饱和度的影响因素分析,分别在研究区采用多元线性回归法求取束缚水饱和度模型和BP神经网络预测束缚水饱和度。

1 区域地质概况

1.1 储层岩性、物性特征

南苏丹P区块发育2套主力含油层系Yabus组与Samma组,其岩石类型主要为砾岩、含泥砾粗砂岩、中细砂岩、粉砂岩和泥岩,其中以含泥砾粗砂岩、中细砂岩为主。通过对该研究区431个岩心样品点物性进行统计分析,其孔隙度分布在8.1%～41.6%,主要在25%～35%;渗透率跨度较大,分布在(0.005～36 133)×10-3μm2,主要集中在(100～10 000)×10-3μm2。结果表明,南苏丹P区块目的层属于高孔隙度高渗透率储层,孔隙度值与渗透率值变化范围很大。

1.2 黏土矿物特征

统计分析表明,研究区黏土矿物以高岭石为主,伊利石次之。研究区高岭石常常以书页状、块状及蠕虫状集合体赋存于次生溶孔或原生粒间孔中,易引起孔隙堵塞,使束缚水饱和度增大;伊利石黏土质点小,可自成蜂窝状微孔隙,呈网状、絮状及发丝状分布于岩石孔隙中,有的包裹在岩石表面,具有较强的吸水性,可吸附大量的水,造成束缚水饱和度增大[4]。

1.3 束缚水饱和度特征

通过对取心岩样做压汞实验,对得到的束缚水饱和度统计分析,束缚水饱和度分布在8%～79.8%,其中大部分值分布在15%～30%。束缚水饱和度的大小和研究区高孔隙度高渗透率储层油水评价、水淹级别划分以及剩余储量计算有着密切的关系。因此,研究束缚水饱和度和建立适合于研究区高孔隙度高渗透率储层的束缚水饱和度模型具有重要的现实意义[5]。

2 单因素分析

大量研究表明束缚水饱和度受多种因素控制,不仅与储层的泥质含量、岩石颗粒的粗细有关,而且与储层的孔隙结构有着十分密切的关系[6]。

2.1 泥质含量对束缚水饱和度的影响

在研究区高孔隙度高渗透率储层岩石中,泥质主要以3种形式存在:分散泥质、层状泥质和结构泥质。分散泥质分布在砂岩颗粒的表面,其体积占据了粒间孔隙的一部分,不承担上覆层压力,束缚水含量较多;层状泥质在砂岩中呈条带分布,其体积取代了一部分砂粒及粒间孔隙,孔隙度降低,使得束缚水饱和度上升;结构泥质指泥质呈颗粒或结核状分布在砂岩中,其代替了部分砂岩而不影响岩石的粒间孔隙,这部分泥质对束缚水饱和度影响不大[6-7]。根据图1,由研究区岩心分析所建立的束缚水饱和度与泥质含量的关系可以看出,束缚水饱和度随着泥质含量的增大而增大。

图1 束缚水饱和度与泥质含量关系图

2.2 粒度中值对束缚水饱和度的影响

岩石颗粒的粗细往往采用粒度中值Md表征,粒度中值指累积曲线上与累积百分含量为50%处相对应的粒径。大量实际资料和数学统计表明,在高孔隙度高渗透率储层中,粒度中值与自然伽马有较好的相关性[8]。本文通过实验数据建立粒度中值与束缚水饱和度关系图(见图2),说明束缚水饱和度随着粒度中值增大而减小。

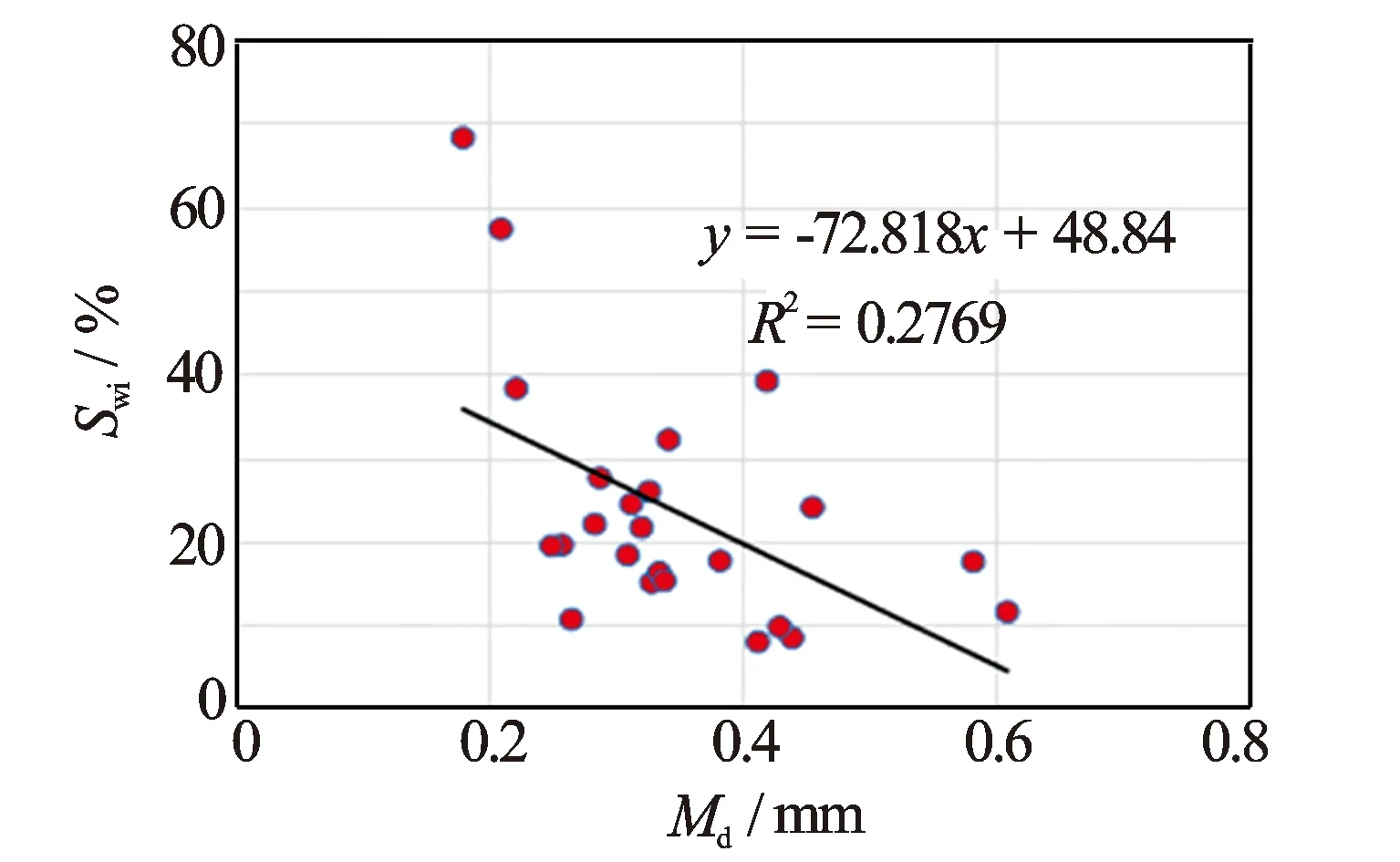
图2 束缚水饱和度与粒度中值关系图

2.3 孔隙结构对束缚水饱和度的影响

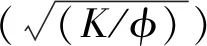
图3 孔隙结构指数与束缚水饱和度关系图

3 多元线性回归建立束缚水饱和度模型

研究发现岩石颗粒粗细对束缚水饱和度有一定影响,而黏土含量和孔隙结构对束缚水饱和度影响相对较大。一般来说,黏土颗粒表面均带负电荷,水分子在岩石中是一种极性分子,对外显示正、负极性。因此,黏土颗粒表面能直接吸附极性水分子,这部分被吸附的水分子称为吸附水;同时被黏土表面吸引的阳离子又可以与极性水分子结合形成水合离子,与阳离子结合的极性水分子称为结合水。就这样吸附水和结合水在黏土颗粒的表面形成了一层水膜,即使黏土含量不高,但黏土颗粒比面大,形成的束缚水也不可忽视[11-12]。分析发现,在同一储层中,有时候相同的孔隙度渗透率却差了几个数量级,这往往是孔隙结构不同引起的。研究表明,岩性越复杂孔隙结构的差异越大,束缚水饱和度的研究越困难。因此,在研究束缚水饱和度模型时,利用泥质含量、孔隙结构,采用多元线性回归分析方法建立模型。

回归模型为

R=0.7968

(1)

式中,Swi为束缚水饱和度,%;K为渗透率,×10-3μm2;φ为孔隙度,小数;Vsh为泥质含量,小数。

4 BP神经网络预测束缚水饱和度

神经网络目前在各个领域的应用都较为广泛,BP神经网络是其中比较常用且比较成熟的一种。它是一个有监督训练的多层神经网络算法,每一次训练对(输入与输出)在网络中经过2遍递算:从输入层开始,经过多层传递、处理,产生1个输出,求出该计算输出与希望输出之差的误差矢量;第2遍反向传播计算,从输出层至输入层,利用误差矢量对权值进行逐层修改[13-14]。由于其特殊的网络结构,具有实现任何复杂非线性映射的功能,适合于求解内部机制较为复杂的问题,在研究区高孔隙度高渗透率储层的背景下,对于束缚水饱和度的预测有着很好的应用前景。

4.1 BP神经网络基本原理

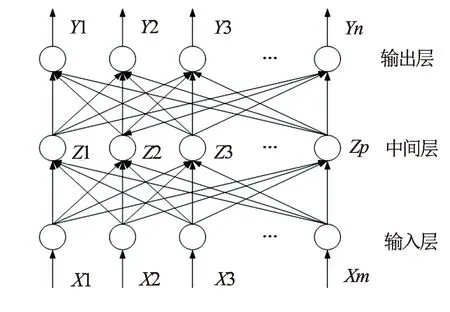
图4 BP神经网络拓扑结构图

BP神经网络是一种按误差反向传播训练的多层前馈网络。它采用梯度下降法计算目标函数的最小值,具有任意复杂的模式分类能力和优良的多维函数映射能力,包含多个输入节点,在经由隐含层加权计算后,将误差反向传播,对非线性结构不断进行优化,将复杂的非线性映射关系简化,最终实现输入参数和输出参数的完美映射。基本的BP算法包含前向传播与误差的反向传播2个过程(见图4),信号输入后逐层加权向前传输,再将输出值与期望值对比计算误差,然后误差逐层反向传播调整计算权值,经过不断的调整权值,使输出值与期望值的误差越来越小,直至误差小于设定的误差值或者达到最大运算次数,此时运算结束得到输出值[15-17]。

图5 BP神经网络拟合分析图

4.2 束缚水饱和度预测模型

BP神经网络进行非线性函数拟合时,拟合结果取决于训练样品的质量,样品既要保证其真实性与可靠性,又要保证在研究区具有代表性和广泛性[18]。本文首先对研究区5口取心井的测井曲线进行标准化,整理了124个样品点,从中随机筛选出104个样品组成训练样本。根据研究分析选取泥质含量、孔隙度、渗透率以及粒度中值作为输入曲线,其中泥质含量由中子-密度测井求得,孔隙度由拟合的密度—孔隙度交会图模型求得,渗透率由拟合的分层段孔隙度—渗透率交会图模型求得,粒度中值由自然伽马求得。为防止数据本身的差异对计算结果造成不必要的误差,对样本数据进行归一化处理,归一化后数据值分布在[-1,1]。学习训练的极限误差设为0.000 1,学习率设为0.01,最大循环次数500次,BP神经网络预测模型的结构为4×10×1。输入样品训练完毕后,用剩余的20个样品点对神经网络进行验证。

整体训练结束后,对该神经网络模型进行分析,总体拟合优度为88.528%(见图5),将通过模型获得的实际输出与期望输出进行对比,模型预测结果的最大相对误差为4.8%。研究表明,通过泥质含量、孔隙度、渗透率和粒度中值可以很好地预测束缚水饱和度。

5 应用实例

在研究区X1井中分别对孔隙结构模型、多元回归模型和BP神经网络3种束缚水求取方法进行了验证(见图6)。对比发现孔隙结构模型计算束缚水饱和度符合率较低,误差较大,平均绝对误差为12.46%,平均相对误差为49%。多元回归拟合考虑到孔隙结构指数与泥质含量的影响,符合率相对于孔隙结构指数模型有一定的提升,大多数点的误差都控制在较小的范围内,但仍有部分点与岩心束缚水饱和度相差较大,平均绝对误差为4.73%,平均相对误差为19%。相比而言,BP神经网络在预测束缚水饱和度有着更好的符合性,95%以上的岩心样品的绝对误差值均在5%以内,平均绝对误差为1.17%,平均相对误差为6.45%。

图6 X1井应用实例*非法定计量单位,1 ft=12 in=0.304 8 m,下同

将BP神经网络应用于生产井中,以研究区X2井为例(见图7),在1 309.7～1 314.8 m井段,该段自然伽马值降低、自然电位异常幅度降低、电阻率降低、深浅侧向电阻率测井差异不明显,该层段孔隙度值为29.21%,渗透率为1 346.25×10-3μm2,含水饱和度在70%左右,采用BP神经网络求取的束缚水饱和度在26%左右,根据研究区水淹评级标准,综合解释为强水淹层。分层生产资料显示,该层日产油13.88 m3,日产水145.67 m3,产水率91.3%。解释结论与生产结果相符,表明BP神经网络预测束缚水饱和度在研究区高孔隙度透率高渗储层中应用效果很好。

图7 X2井应用实例

6 结 论

(1)南苏丹P区块储层属于高孔隙度高渗透率储层,具有孔隙度、渗透率及束缚水饱和度变化范围大,孔渗结构复杂等特点,岩性以含泥砾粗砂岩、中细砂岩为主,黏土矿物以高岭石为主,伊利石次之。

(2)束缚水饱和度的大小很大程度上受到岩石内在因素影响,主要与泥质含量、粒度中值、孔隙结构有关。

(3)从研究区高孔隙度高渗透率储层实际情况出发,对束缚水饱和度的影响因素作单因素分析,然后应用多元线性回归和BP神经网络建立了2种束缚水饱和度模型,在研究区X1井中验证分析。单因素孔隙度指数建立的模型符合度较差,误差较大,平均绝对误差为12.46%;多元回归拟合模型符合度较好,误差控制在较小的范围内,平均绝对误差为4.73%;BP神经网络预测符合度最好,平均绝对误差为1.17%。

(4)研究区X2井应用BP神经网络预测的束缚水饱和度模型后,结果表明,解释结论与生产动态资料相符,应用效果好,可在研究区广泛推广使用。