元素录井确定矿物含量多种方法对比研究

黄秋静,孙建孟,王海青

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.山东立鼎石油科技有限公司,山东东营257000)

0 引 言

X射线荧光录井技术是以X射线荧光分析理论、岩石化学理论为基础,在钻井过程中通过对钻井岩屑的X射线荧光分析获得地层岩石元素含量,并根据元素和元素组合特征的变化进行岩性识别和地层评价的井筒勘探技术[1-2]。研究表明,自然界中各元素、矿物的丰度差别很大,如果按元素克拉克值顺序排列,前8种元素(O、Si、Al、Fe、Ca、Na、Mg、K)就占地壳总量的98%以上,因此,也被称为造岩元素;沉积岩中前8种矿物的总量就达到97.5%以上(其中石英含量约为31.5%,碳酸盐矿物含量约为20.5%,云母与绿泥石含量之和约为19%,玉髓含量约为9%,黏土矿物含量约为7.5%,长石含量约为7.5%,氧化铁含量约为3%)[3]。因而地层中几种主要元素构成了主要的造岩矿物。这些元素与矿物之间有非常密切的关系,在地层中,矿物的化学组成是固定的,其中所含各元素的含量百分比也基本恒定[4]。以此为基础,通过建立元素和矿物之间的转换关系求取矿物含量。

转换过程的关键是寻找元素到矿物间的合适转换关系,进而通过一定的数学算法求解矿物含量。1986年,Herron通过地球化学测井得到的元素含量计算得到了矿物含量。Herron通过大量的实验与统计建立了简单的转换模型,通过Al、Fe和K元素的含量计算得到了高岭石、伊利石和钾长石的含量,与真实值对比精度较高,从而证明了元素和矿物之间定量关系的存在[5-6]。本文在Herron所提出的转换关系模型基础上,对长庆油田×井进行模型改进和实际应用,并补充了氧化物闭合模型法和神经网络法,最后与该井全岩分析数据对比,分析实际计算效果。

1 5种矿物求解方法的基本原理模型与处理结果

1.1 数据处理

进行元素定量反演矿物之前,需要对所求目的层XRF元素含量和全岩分析矿物含量进行数据预处理[7]。X射线荧光录井仪可以测量从钠(Na)到铀(U)等34种元素化合物的质量百分含量,通过数值单位为“脉冲/s”的X射线脉冲数记录元素产生的荧光能量和强度。该数值不能定量描述元素真实含量值,但能定性指示元素含量的高低[8],通过国际样对其进行标定,确定脉冲数与质量分数的关系,能够实现对元素质量分数的测量[7]。

由于X射线荧光录井得到的数据是单个元素在地层中的化合物质量分数,在计算前应进行归一化处理。根据自然界元素分布规律、全岩分析矿物类型和XRF元素含量筛选出主要影响元素,将Si、Al、Fe、Ca、Na、Mg、K这7种XRF测量的主要元素氧化物分别按照二氧化硅(SiO2)、三氧化二铝(Al2O3)、碳酸亚铁(FeCO3)、碳酸钙(CaCO3)、氧化钾(K2O)、碳酸镁(MgCO3)、氧化钠(Na2O)进行100%归一化处理后,再反算单元素质量百分含量进行计算处理。

1.2 氧化物闭合模型法

岩石中主要元素的氧化物近似相对分子质量,在某种程度上可以反映岩石中的矿物组成。氧化物闭合模型法原理是假定组成矿物的氧化物、碳酸盐含量和石英、长石、云母的混合物(QFM)的质量百分数之和为1,以此反解3种矿物类型。

在转换矿物含量过程中,需要选择矿物的特征元素。如石英(SiO2)的特征元素选为Si元素,方解石(CaCO3)的特征元素选为Ca元素,白云石(CaMg(CO3)2)的特征元素选为Ca和Mg元素,黄铁矿(FeS2)和菱铁矿(FeCO3)的特征元素选为Fe元素,黏土矿物中的化学组成比较复杂,但是经研究发现,Al元素与黏土矿物有很好的相关性,所以可以选择Al元素作为黏土矿物的特征元素[9-10]。Fe元素和很多矿物有关联,包括菱铁矿、黄铁矿、伊利石、高岭石和海绿石等,但主要存在于菱铁矿和黄铁矿等铁矿石中,黏土矿物只含有少量铁元素。Ca元素主要与碳酸盐矿物关系密切,黏土矿物中只含有极少量的Ca元素。

(1)估算黏土含量。对该地区的地质资料进行分析可知,主要的黏土矿物由高岭石组成。已知Al、Si、Fe、Ca、Mg对黏土含量相关性较为明显,可以通过数理统计方法建立黏土含量计算模型

WClay=0.0102(WAl+WSi+WFe)/(WCa+

3WMg)+7.6298

(1)

利用所建立模型计算×井黏土含量,与全岩分析值进行对比[见图1(a)],计算值与全岩分析值位于45°线两侧,两者相关性较好,说明模型可靠。

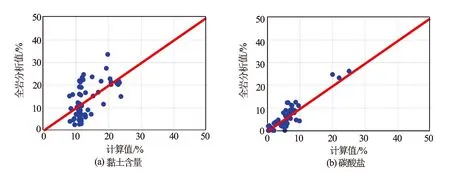
图1 黏土与碳酸盐含量估算效果

(2)估算碳酸盐含量。碳酸盐矿物主要包括方解石和白云石,方解石的主要组成元素是Ca元素,白云石的主要组成元素是Ca和Mg元素。同样,建立碳酸盐计算模型

WCar=1.0801WCa+0.9472WMg-1.3252

(2)

利用所建立模型计算×井碳酸盐含量,与全岩分析值进行对比[见图1(b)],计算值与全岩分析值位于45°线两侧,两者相关性较好,说明利用模型计算碳酸盐含量是合适的。

(3)估算QFM含量。地层中剩余的部分为砂质部分,主要包括石英、长石和云母(QFM),该部分估算公式为

WQFM=100-WClay-WCar

(3)

该方法确定的矿物含量是岩石骨架矿物含量,单位是重量百分含量而不是体积百分含量。它的计算方法简单,但是反演出的矿物种类有较大局限,只能粗略的划分计算3大类矿物(黏土、碳酸盐、QFM)。

(4)氧化物闭合模型法处理结果分析。在上述模型基础上,对长庆油田×井2个目的层进行处理分析。其中,黏土含量主要由高岭石组成;灰质含量为碳酸盐矿物,主要包括方解石和白云石;剩余部分为砂质含量,由石英、长石、云母的混合物组成。计算结果见图2,其中红色杆状线为全岩分析得到的元素含量,绿色曲线、蓝色曲线、粉色曲线分别为计算出的黏土、QFM、碳酸盐岩含量。可见,氧化物闭合模型计算结果与全岩分析结果吻合性较好。

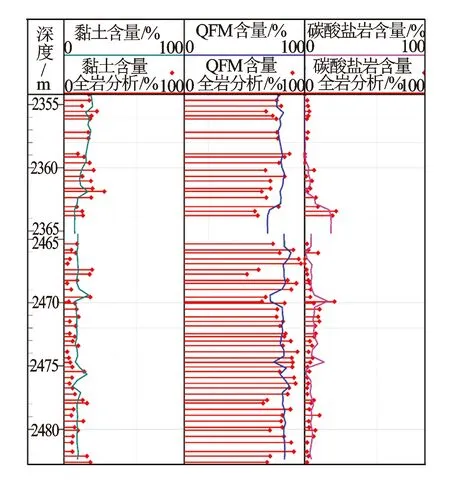
图2 氧化物闭合模型法计算结果与全岩分析矿物含量对比图

1.3 基于Herron模型的4种线性求解方法

Herron等提出,元素含量与矿物含量之间的相关关系,可以用矩阵的形式表示

(4)

式中,Ei为第i种元素的含量;Cij为第j种矿物中第i元素含量,是元素含量与矿物含量的转换系数,也是该方法关键点之一;Mj为第j种矿物含量。

通过对式(4)求逆,用元素百分含量得到矿物百分含量

[M]=[C]-1[E]

(5)

式中,[C]-1为转换系数矩阵的逆矩阵。

非负最小二乘法、截断奇异值分解法和线性规划法这3种方法在Herron模型的基础上,针对区块实际情况,选择元素种类,确定转换系数,运用不同的优化技巧求取矿物含量。神经网络法基于Herron模型元素与矿物之间存在明显线性关系理论,通过构建神经网络模型寻找线性关系进行矿物组分求取。

转换系数矩阵的确定是保证元素反演矿物精度的前提。对研究区地质情况、全岩分析矿物种类和含量分析,通过Th/K交会图确定黏土类型为高岭石,选取Si、Al、Fe、Ca、K、Na、Mg这7种元素含量反演黏土、石英、钾长石、斜长石、方解石、白云石和菱铁矿7种矿物含量,转换系数见表1。

由于适合该地区元素与矿物间的专用转换关系还没有确立,所以首先借助于Herron通用转换系数处理,再根据反演结果与该井岩心数据资料对比进行完善。

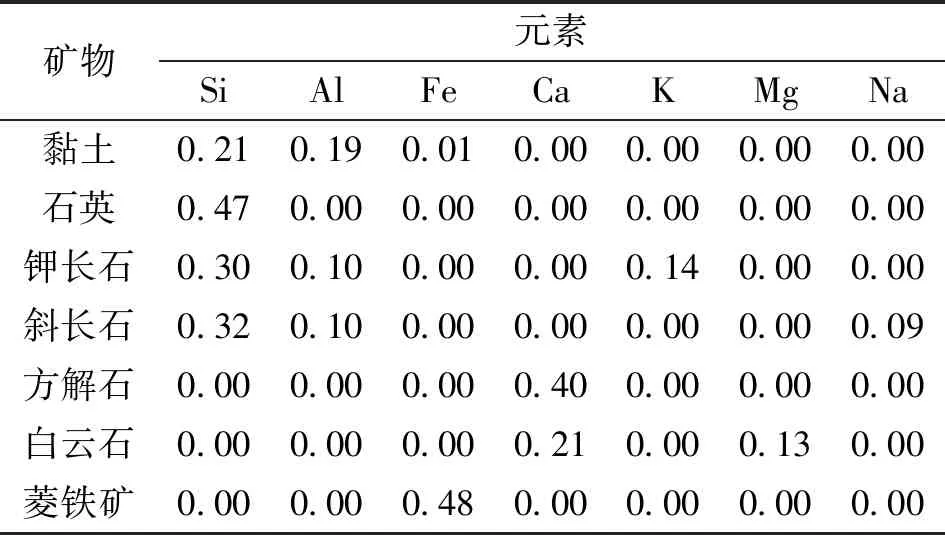
表1 7种元素与7种矿物之间的转换系数表

(1)最小二乘法。元素含量反演矿物含量[E]=[C][M],即求解方程组Ax=b,当方程组为矛盾方程组时,需要求解最优解。最小二乘法是最常用的求解方程组最优解的方法,最小二乘解是计算值与实际值的误差平方和最小时的解

(6)

由于最小二乘法求解的矿物含量存在负值,而实际情况下矿物含量不可能出现负值,因此,对最小二乘法进行优化,通过非负最小二乘法反演矿物含量。非负最小二乘法是最小二乘法一个带约束版本,要求所有系数不能为负,更符合实际情况。

通过非负最小二乘法对井×进行矿物组分计算,处理成果见图3。图3中粉色曲线(NNLS)的反演结果与红色杆状线全岩分析值一致性较好。

(2)截断奇异值分解法。在求解非线性方程组中,用一般的数值解法会有较大的误差,甚至严重失真。造成这一问题的原因是所建立的转换系数矩阵的条件数普遍较大,导致转换关系方程呈病态。为此,本文引入了截断奇异值分解(TSVD)方法[11]。

元素含量反演矿物含量的函数模型为Ax=b(其中A∈Cm×n,b∈Cm给定,x∈Cn待求),得到最小二乘解为

Xis=(ATA)-1ATb

(7)

对矩阵A进行奇异值分解得

(8)

式中,U=[u1,…,un]∈Cm×n,V=[u1,…,um]∈Cn×n均为正交矩阵;ui、vi分别为U、V的第i列;S=diag(s1,s2,…,sn),其中si(i=1,2,…,n)为A的奇异值。将公式(8)代入公式(7)得到

(9)

通过上述的推导可以看出,最小二乘法和奇异值分解法是等价的。当矩阵A是病态矩阵时,矩阵A的奇异值中会有1个或多个接近于0,从式(9)可知,当si很小或接近于0时,最小二乘解的均方误差将会趋于无穷大,尽管它是无偏的,但已经不是最优解了。所以考虑直接去掉那些数值很小的奇异值,可以减小解的均方误差,提高解的精度和增加解的可靠性。

假设矩阵A的奇异值中有n-k个奇异值很小,去掉这n-k个奇异值得到的截断奇异值分解算法的解为

(10)

通过截断奇异值法对井×进行矿物组分计算,处理成果见图3。图3中棕色曲线(TSVD)的反演结果与红色杆状线全岩分析值较吻合。

(3)线性规划法。由于测量、分析等过程存在一定的误差,使得地层元素的真实含量与测量值之间存在残差。如果令残差为Δ,则式(4)应改为

(11)

求解问题转变成求残差平方和最小时的最优解的问题。最小残差平方和可表示为

(12)

由于地层中的矿物含量均大于等于0,且矿物含量总和小于等于1,即

(13)

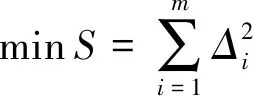
(14)

通过线性规划法对井×进行矿物组分计算,处理成果见图3。图3中蓝色曲线(LP)的反演结果与红色杆状线全岩分析值对应效果较好。

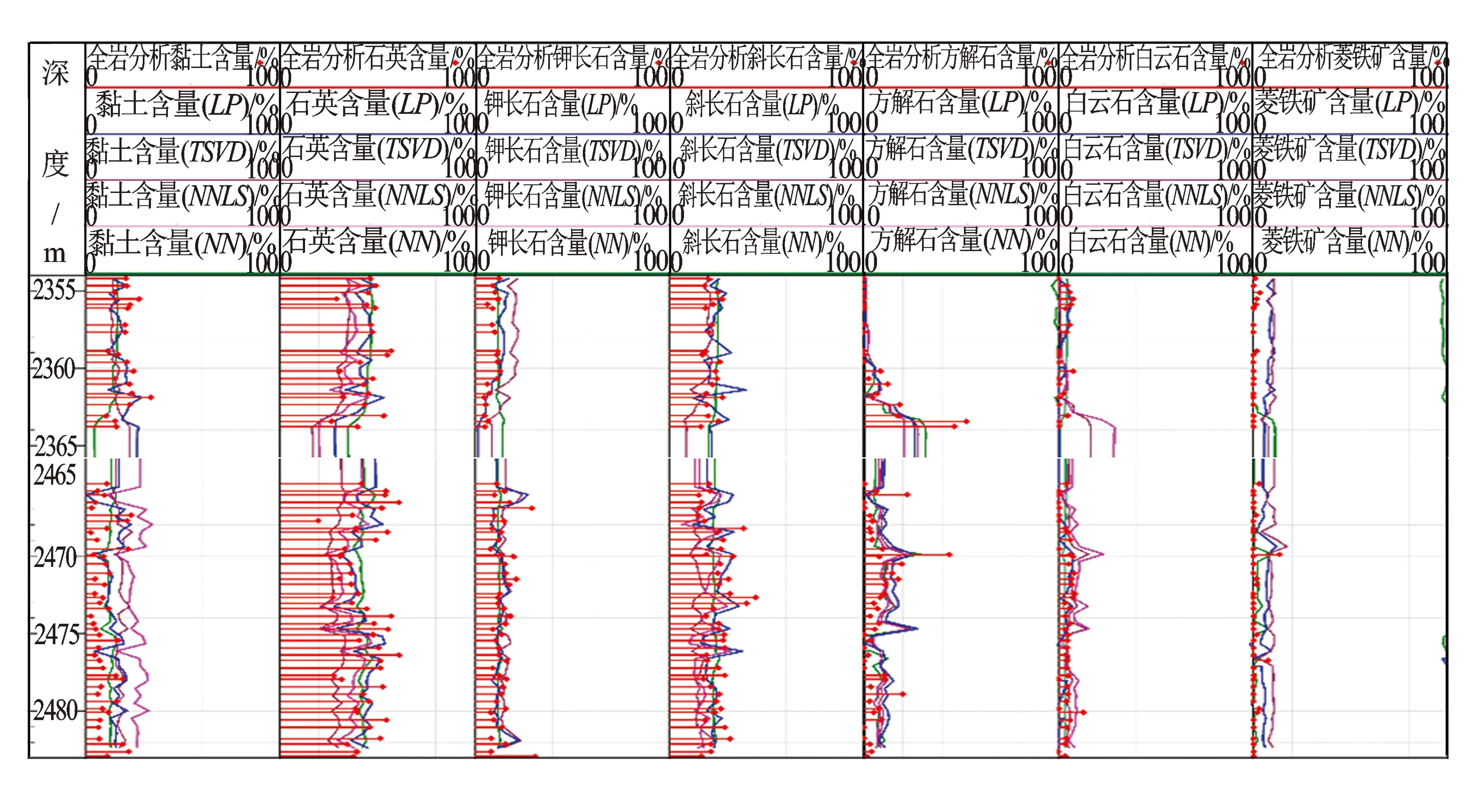
图3 4种数学方法计算结果与全岩分析矿物含量对比图

(4)神经网络法。相较于前几种计算方法,神经网络分析法从数学理论上来讲最不严谨,目前也没有相关的严格数据推导。但由于其模拟了人类的思维判断方式,在已知量与未知量关系不明确的情况下有着明显的实用性优势。

实例中的神经网络法借助于Scikit-learn的MLPRegression函数实现。多层感知器(MLP)神经网络能够从数据样本中自动的学习并揭示出样本中所蕴含的非线性关系,可以用于分类、函数逼近、参数估计等问题。因此,采用MLP神经网络对实测岩石主要元素组成样本进行训练,建立网络模型,找寻元素与矿物间的转换关系。多层感知器(MLP)使用输入与输出之间多层加权连接,MLP的结构基本类似于一套级联感知器,该网络可以包含一层或者多层隐藏神经元,这些隐藏层神经元逐步从输入模式中提取多种有用特征,可以处理学习复杂的任务[12]。

选取地层中Si、Al、Fe、Ca、K、Na、Mg这7种元素含量为输入层,黏土、石英、钾长石、斜长石、方解石、白云石、菱铁矿7种矿物含量为输出层。将数据集划分为训练样本、测试样本和保持样本3类,训练集由数据集中随机抽取70%的样本组成,测试集由20%样本组成,另外10%作为保持样本。通过建立3层神经网络结构,其中输入层7个节点,2个隐藏层分别6个节点和4个节点,输出层7个节点,利用神经网络方法,通过元素含量反演矿物含量。

本文采用的多层感知器的优化算法采用调整的共轭梯度算法,隐含层激活函数采用双曲正切函数,其计算公式为

(15)

采用Softmax函数激活输出层函数,双曲正切函数属于S性函数的一种,输入取值范围为(-∞,∞),输出范围为(-1,1),隐含层神经元还可以取Sigmoid函数或者logsig函数,其与双曲正切函数的区别不大,仅在输出范围方面有区别,它的输出值域为(0,1),更符合实际结果。

通过神经网络法对井×进行矿物组分计算,处理成见图3。绿色曲线(NN)的反演结果与红色杆状线全岩分析值对应一致性较好。

(5)4种线性求解方法处理结果分析。4种方法分别计算得到的矿物含量与实际实验室全岩分析结果的对比见图3。图3中红色杆状线是实验室全岩分析所得矿物含量,蓝色曲线是线性规划计算得到的矿物含量,棕色曲线是截断奇异值分解法所得矿物含量,粉色曲线是非负最小二乘法所得矿物含量,绿色曲线是神经网络法计算出的矿物含量。可以看出,4种方法计算出的矿物含量结果与实验室岩心分析得到的结果随地层深度的变化趋势基本一致。其中菱铁矿含量略有差异,神经网络法出现大量负值,可能是由于模型设计不够准确、铁元素含量较低导致误差较大;线性规划法和截断奇异值分解法反演出结果偏大,可能是由于转换系数选取不当,应在后期丰富该地区资料数据之后进行改进。整体来看,线性规划方法结果最佳,特别是黏土含量、钾长石、白云石3类计算结果最符合岩心分析情况;截断奇异值和神经网络法次之,石英含量最符合全岩分析结果;最小二乘法由于奇异值的存在影响误差较大,黏土含量计算结果普遍偏大。

2 基于三端元求解效果

为了实现三端元构成三角形进行岩性自动划分,进一步比较了氧化闭合模型法三组分矿物含量与其他4种方法求解结果。其余4种方法直接求出7种矿物组分,然后合并成三组分进行对比(见图4)。结果表明线性规划法处理效果最佳,计算结果与岩心分析数据匹配性最好,符合实际应用要求。

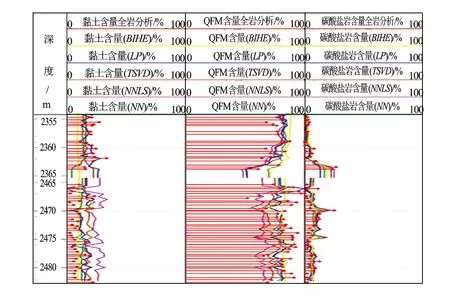
图4 5种数学方法计算结果与全岩分析3大类矿物含量对比图

3 基于三端元反演的岩性自动划分

沉积岩的分类方案有很多种,地质中用到的主要是将沉积岩分为砂岩、泥岩(页岩)和碳酸盐岩3大类[13-15]。通过元素含量反演估算得到了地层主要矿物的含量,主要有黏土(WClay)、碳酸盐(WCar)和石英+长石+云母(WQFM)3种。这3种矿物是地层中的主要造岩矿物,分别是泥岩(页岩)、碳酸盐岩和砂岩的主要造岩矿物,所以可以很据3种矿物的含量区分岩性[16-18],斯伦贝谢公司据此建立了岩性识别三角图版(见图5)。基于三角图版的3个端点定义了12种岩性:泥灰岩、泥岩、页岩、砂质页岩、泥质砂岩、砂岩、纯砂岩、钙质砂岩、钙质页岩、碳酸盐岩、砂质碳酸盐岩、泥质碳酸盐岩[19]。

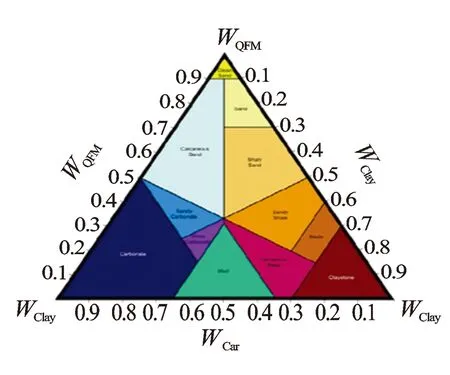
图5 斯伦贝谢公司岩性识别图版

由元素定量反演算法得到矿物含量结合该地区岩性组成进而得出黏土、碳酸盐和石英+长石+云母,编写软件根据三角坐标在图版上进行投点。输入数据后软件自动将三角坐标系中的点坐标转化为直角坐标系的点坐标并点入数字化后的图版,在数据后一栏自动确定岩石类型。将×井通过线性规划方法计算得到的各点矿物含量依次投到图5上(见图6)。可以看出该井岩性主要为砂岩,其中含有少量灰质砂岩。

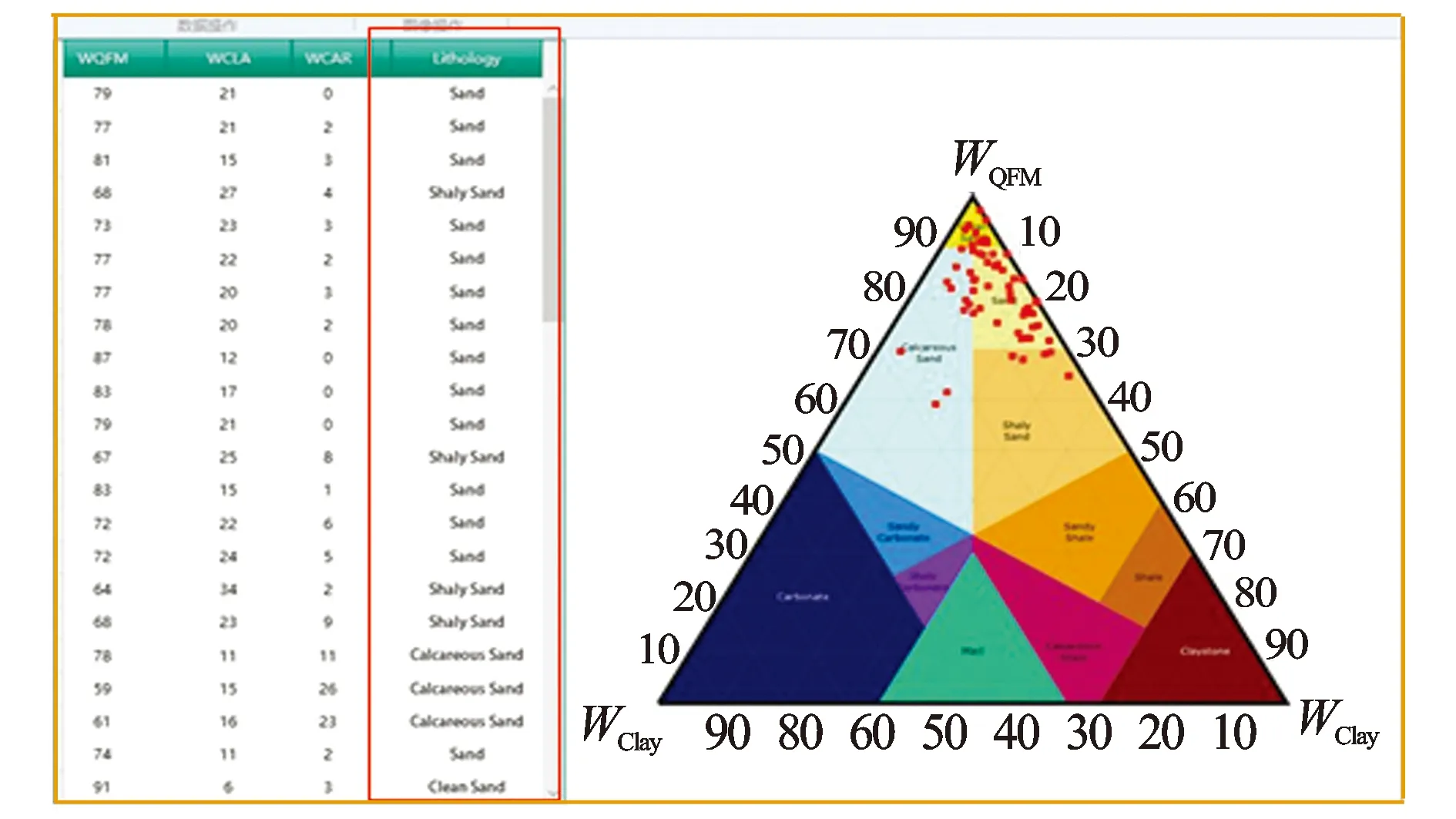
图6 利用软件将×井计算结果在沉积岩岩性识别图版上的投影

将软件识别结果和该井全岩分析得到的岩性结果对比计算可知碎屑岩岩性识别正确率达到89%,出现误差的原因是个别点出现在了2个岩性区域交界线附近,使该点分类结果不准确。运用该方法可以快速识别、划分目的层岩性情况。

4 结 论

(1)氧化物闭合模型法计算简单,且适用性较广,可以在大部分沉积岩地层使用,但是只能粗略划分3种大类矿物含量。

(2)最小二乘法主要适用于方程数多于未知量数情况,即元素种类多于矿物种类,此时转换方程为超定方程。非负最小二乘法要求所有系数不能为负,更符合实际情况。

(3)截断奇异值分解法可以解决转换系数为病态矩阵的问题,该方法要求已知元素种类不少于待求矿物种类。在求解最优解时直接去掉数值很小的奇异值,减少解的均方误差,提高解的精度和可靠性,但也会由于奇异值的截断忽略一些特征点。

(4)线性规划法通过设定目标函数和约束条件来求取矿物含量。该方法对元素和矿物个数的多少没有明确要求,理论上更适合解决实际问题,该方法重点是建立最优的数学模型,需要进行大量的工作来计算、分析和对比。

(5)神经网络法通过对构成矿物的元素进行敏感性分析,选择敏感元素作为神经网络输入,选择主要矿物作为神经网络输出建立网络结构进行矿物含量求取,在有大量数据支持的情况下可能得到更好的反演效果。