一种基于网格延展法的等值线生成算法
陈 胜 ,黄诗峰 ,臧文斌
(1. 中国水利水电科学研究院,北京 100038;2. 水利部防洪抗旱减灾工程技术研究中心,北京 100038)
0 引言
等值线在水利信息化系统和科学研究中有着广泛的应用,是数据可视化的重要手段之一。通过雨量等值线可以表达降雨量的空间分布特性[1];通过地下水埋深等值面可以实时掌握地下水动态,为水资源开发、水资源量管理提供依据[2-3];通过旱情等值线分布,可研究和监测旱情的时空分布与演变[4]。等值线是将有限的观测点数据,通过专门的等值线算法生成图形数据,用于表达数据在空间的分布特性。
等值线生成算法从生成方法上分主要有基于三角网[5]和规则网格[6]2 种生成算法。基于三角网的算法计算效率高、精度高,但算法实现过程比较复杂,当数据点分布不规律时容易出现异常,如出现等值线交叉、分叉等现象;基于规则网格的算法计算方法简单,但是精度不够高。已有的研究中二者在等值线追踪方面都需要考虑等值线交叉、连通域等问题。在生产应用中基于三角网进行等值线计算的算法,因为算法比较复杂,往往需要借助第三方软件和组件实现,如 ArcGIS,MapX,Surface等[7-9]工具软件中包含等值线组件,处理过程不但需要考虑如何在算法组件和应用系统之间进行集成,而且在实际应用时常常出现因为数据点分布原因表现出的算法健壮性不够的情况,比如出现等值线交叉,等值面局部区域缺失等异常现象。等值线的生成算法近几年研究较少,等值线的生产应用及相关问题的研究解决近几年相对较多。
本研究立足于水利信息化生产应用,考虑降雨和水资源分布 2 类等值线,主要用于表达和分析降雨量、水资源的宏观分布,并不需要很高的精度,同时数据点空间分布也不规律。因此研究一种基于网格延展法的等值线算法,目标是使等值线算法简单、健壮,易于实现,并能够满足生产应用的需求。
1 算法原理
网格延展法是一种基于规则网格的等值线生成新方法,该算法没有采用已有三角网或规则网格等值线生成研究中的基于线的追踪方法,而是利用研究区域内同一等值面在网格空间上是连续分布这一特性进行研究的,从研究区域内部的一个网格点向四周进行递归搜索,可以延展到研究区域内的其他所有连通且取值范围相同的网格点,从而形成一个等值面。采用网格延展法生成等值线的基本流程如图1 所示。

图1 基于网格延展法的等值线生成过程
1.1 研究区域网格构建
基于网格延展法生成等值线,首先构建用于等值线计算的规则网格,网格的范围应覆盖整个研究区域,研究区域往往是某一区域的行政边界或某一流域的边界。整体网格的外包络矩形记录有地理坐标信息,便于最终生成的等值线从网格坐标转换为地理坐标。网格的精度根据实际应用需要确定,网格数目越大生成的等值线越细致,但需要耗费的计算量也越大。实际应用研究表明,对于雨量等值线来说,一般生成规模为 1 000×1 000 的网格即可满足生产应用需求。研究区域网格在算法程序中表示为一个二维数组,为提高算法效率可以创建整数类型的二维数组存储网格信息,这样可避免浮点类型的计算,减少运行内存的开销,等值线的计算效率会有明显提升。基于网格延展法的等值线算法程序中需要构建多个同等大小的辅助网格,用来保存边界标记信息、中间计算成果等。
1.2 等值线边界确定
等值线边界确定是为了将等值线的计算限定在一定的边界范围内进行,不同于已有研究中先生成等值线再根据边界裁剪的确定方法。
多数已有的等值线生成算法研究中,一般是先生成 1 个较大区域(如等值线外包络矩形)的等值线,然后根据某一区域的行政边界或某一流域的边界进行裁剪,得到指定边界范围内的等值线。基于网格延展法进行等值线计算时,将等值线生成计算限定在研究区域边界范围内进行,这样可避免复杂的等值线裁剪计算过程,也省去无效区域的计算工作量。边界数据一般为 1 组矢量数据,如 ArcGIS 里的面状图层,是由折线(折线由点序列构成)构成的不规则多边形,截取的其中一部分如图2 中的线段所示。此时需要将这些折线对应到网格上,并形成连续的封闭区域作为等值线计算的范围。

图2 等值线边界栅格化
本研究通过对研究区域边界数据进行栅格化处理和标记,从而在构建的网格上形成连续的封闭区域。算法步骤如下:
1)步骤 1。在研究区域边界点序列上任取一点作为初始点,将初始点的坐标转换为网格坐标并标记为一个起始的边界网格点。因为网格坐标是整数,所以边界点地理坐标转为网格坐标时,因为要进行取整计算,故会产生一定的误差。
2)步骤 2。在研究区域边界点序列上取下一个点坐标并转为网格坐标,此时需要判断 2 个网格点之间应该是哪些栅格点需要标记为边界网格点。本算法计算时首先将 2 个点的网格坐标连成一线,如图2 中的 P1和 P22 个点(P1,P2为构成失量边界点序列中相邻的 2 个点),得到 P1到 P2网格 2 个方向的梯度变化 Δ x 和 Δ y,以 P1点为起点向 8 个方向移动 1 个网格,分别计算各个网格点到 P1的梯度变化 Δ xn和 Δ yn,将梯度变化最接近 P1到 P2的网格标记为边界网格,即将 (Δ y/Δ x - Δ yn/Δ xn)min的网格点标记为边界网格点,记为 Pn。再以 Pn为起点向 8 个方向移动 1 个网格,分别计算各个网格到P1的梯度变化 Δ xn和 Δ yn,得到下一个边界网格点,直至 Pn到达 P2点,从而形成 P1到 P2所有边界网格点的标记。
3)步骤 3。将 P2点作为 P1,从研究区域边界点序列中取下一个相邻的点作为 P2,重复步骤 2,直至矢量边界的点序列处理完成。
完成这几个步骤后所有标记为边界的网格点形成一个闭合的区域,该区域等值线生成计算的范围。
1.3 网格插值计算
插值计算中网格范围的确定、等值面的提取、重分类等等值线生成重要计算步骤都应用了网格延展法,体现了算法过程简单易行、健壮性等特点。
网格插值计算并不是对所有的网格点都进行插值计算,所以首先要确定待插值网格。网格延展法利用需要插值的网格区域是连续分布的特性,从确定边界区域内任选一点,并递归遍历及插值计算所有待插值的网格点。待插值网格点确定的递归搜索算法步骤如下:
1)步骤 1。从边界标记区域内 1 个网格点开始向该栅格点的 4 个方向搜索,如果存在相邻网格点且不是边界标记网格点(同样未被标记为待插值网格)则标记为待插值网格点,并加入到递归搜索的网格点队列中。
2)步骤 2。从递归搜索网格点队列中选取 1 个网格点为起点向 4 个方向查找,如果存在相邻网格点且不是边界标记点(且是未被标记为待插值网格)则标记为待插值点,同时加入到递归搜索网格点队列中。如果当前搜索的网格点 4 个方向都没有找到新的待插值网格点,则将该网格点从递归搜索网格点队列中删除。
3)步骤 3。如果递归搜索网格点队列已经为空,则搜索过程结束,否则转向步骤 2。
网格点的递归搜索步骤和结果如图3 所示。图3 a 中编号为 1 的点表示递归搜索的起始网格点,数字 2 表示递归遍历的第 2 步,以此类推,最终形成图3 b 所示的递归搜索结果,每个数字表示递归搜索的次序。对所有待插值的网格点进行空间插值计算,以雨量等值线生成为例,网格插值计算是根据雨量观则站点的数据对研究区域内的所有网格进行插值计算。空间插值算法有克里金(Kriging)、反距离加权平均(IDW)、样条函数等算法[10],本研究选用反距离加权平均插值算法作为插值方法,实际应用时可根据实际需要替换为其他插值算法。

图3 网格点的递归搜索
反距离加权平均算法基本公式如下:

1.4 插值结果重分类
重分类是根据空间梯度的展示需求对网格的数值进行重新划分,1 个分类值代表1 个取值范围,提取相邻的且分类相同的 1 组网格就是 1 个等值面,这不同于已有研究中一般通过等值线追踪生成等值线的方法。
重分类算法是将插值后的数据按照一定条件进行归类,每一类代表该等值面的取值范围。重分类的每一个类别的取值范围可以根据空间梯度的应用需求进行定义。比如雨量等值面中 0~10 mm 雨量的网格点归为一类,10~20 mm 雨量的网格点归为一类,以此类推。当研究区域内某些位置的空间梯度很大导致等值线分布较密集时,由于网格化坐标带来的误差可能会略过一些中间取值范围的等值线,无法表现等值线的细部分布特点,但这种方法生成的等值线不影响宏观信息分布的表达,也不会有常规等值线生成算法追踪过程出现的等值线交叉现象。重分类算法比较简单,计算时将所有插值计算网格点遍历 1 次,按照指定的重分类条件对网格进行重新赋值。
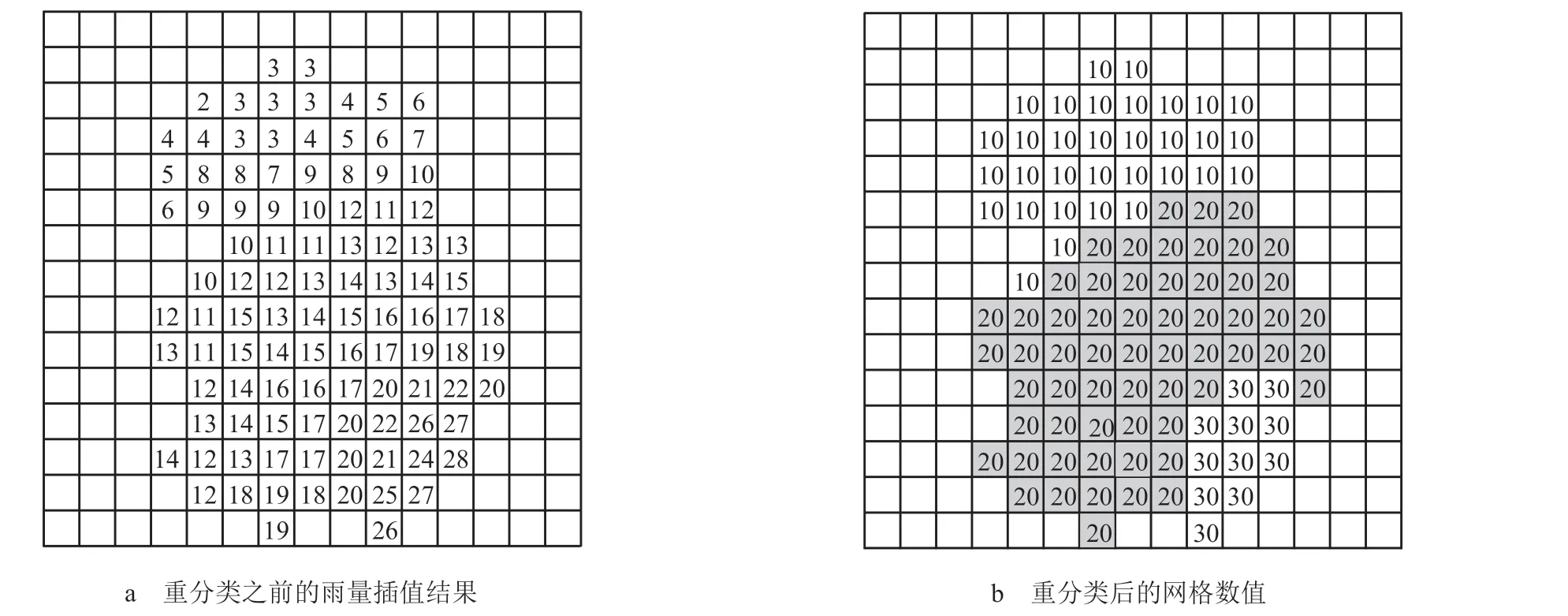
图4 插值结果重分类
图4 a 是插值后的网格数值,网格中的每个数字代表每个网格的雨量值;图4 b 是重分类后的网格数值,网格中的数字代表该网格所属于的分类,属于同一分类的代表取值范围相同的网格点。从图4 b 可以看出同一分类所有网格构成的连续区域即为一个等值面。
1.5 等值线边界追踪
等值线边界追踪即通过算法得到同一分类且连续的所有网格点所构成的边界。然而等值线的边界往往很不规则,需要通过一定的算法追踪确定。本研究同样通过网格延展法将每个等值面的网格点先提取出来,然后对这些网格的外包络边界进行追踪。基于网格延展法追踪等值线的算法步骤如下:
1)步骤 1。使用网格延展法从重分类结果网格中提取分类值相同且连续分布的所有网格点,提取时从研究区域范围内任意一个点开始,以该点为起始点向四周递归搜索所有分类值相同的网格点,得到分类值相同且连续的所有网格点。同时将这些网格点在重分类结果中标记为已空网格,从而避免此后被再次提取。提取的网格点放入一个新的临时网格中(与原始构建的网格大小一致,所有其他网格标志为空网格)进行处理。
2)步骤 2。从步骤 1 的临时网格中选取 1 个边缘网格点的边作为起始边。识别起始边时,可以从网格中的 1 个空白网格向有数值的网格区域进行遍历查找,碰到的第 1 个边即为该等值面的起始边(起始边一边的网格有数值,另外一边的网格标志为空),并将该起始边加入到边界结果队列中。以起始边为起点向 4 个方向搜索下一个边,不在边界结果队列中且为边界边的网格边即为下一个符合条件的边界边,同样加入到边界结果队列中。以此方式继续搜索,直至所有的边界遍历完成(即遍历到达起始边),边界结果队列中所有的边界数据构成一个等值面的边界。某一等值线追踪计算的结果如图5所示,粗线的所有网格边构成一个等值面边界追踪的结果。
3)步骤 3。重复步骤 1~2 直至所有的重分类结果被提取完,则完成等值线边界的追踪计算。
1.6 等值线平滑
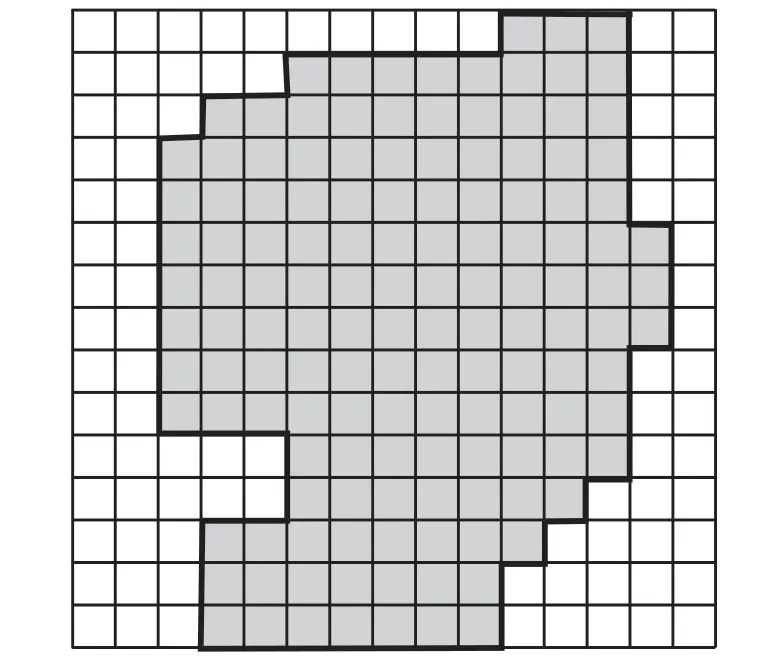
图5 等值线边界追踪结果
由网格边界追踪直接形成的等值线在视觉上不够平滑,所以需要对等值线追踪结果进行平滑计算。等值线的平滑算法既要达到平滑效果,还要保证平滑后的等值线之间不能发生交叉现象。本研究使用一种简单的平滑算法,可以消除梯形边界,也能保证等值线的边界平滑后不相交,满足大多数应用场合对等值线平滑的要求。
简单的平滑算法是逐段将等值线边界追踪结果的每个边界边的中点依次连接起来,形成一个新的边界边,新生成的边界从视觉上显得更加平滑。研究区域内所有的等值线使用同样的平滑算法,这样平滑后的边依然是相切的,不会出现等值线相交现象。图5 所示的等值线追踪后的原始网格边界构成的梯形比较明显,经过一次平滑处理后得到的边界结果如图6 所示,如果需要更平滑的效果可以连续进行多次平滑。

图6 等值线的平滑处理结果
2 算法应用
基于网格延展法生成等值线算法主要的操作是对规则网格的操作,即对二维数组的操作,所以可以使用 C#,Java,JavaScript,Python 等多种语言实现。本研究使用 Java 语言实现等值线算法,形成一个可供水利信息化应用系统直接调用的算法组件。该算法组件在不需要安装 GIS 软件或等值线组件的情况下,可以根据雨量站和研究区域边界等数据生成等值线,并能方便和应用系统进行集成。
以北京市怀柔区雨量等值面为例,其网格规模设定为 1 000×1 000,雨量观测站点为 26 个,雨量站点信息及监测数据由北京市怀柔区水务局提供。等值面边界为北京市怀柔区的行政区边界,提取自全国 1∶250 000 水利电子地图,边界为 Shp 格式的矢量面状图层。等值线算法组件依据边界点序列,得到研究区域网格的坐标范围为东经 116°17′~116°63′,北纬 40°41′~41°4′,以该坐标范围构建矩形网格区域。然后根据边界点序列数据在网格上进行边界标记,再根据 26 个站点的雨量数据进行空间插值,得到边界范围内每个网格的值。按照雨量 0~100 mm范围内每隔 10 mm 为 1 个分类,100 mm 以上单独作为 1 个分类,对边界范围内所有网格点进行重分类计算。将等值线追踪结果按照本研究的平滑算法处理 3 次,最终生成的北京市怀柔区雨量等值线、面如图7 所示。
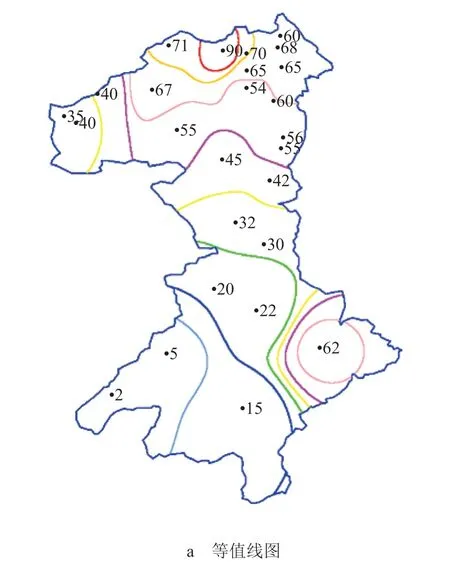
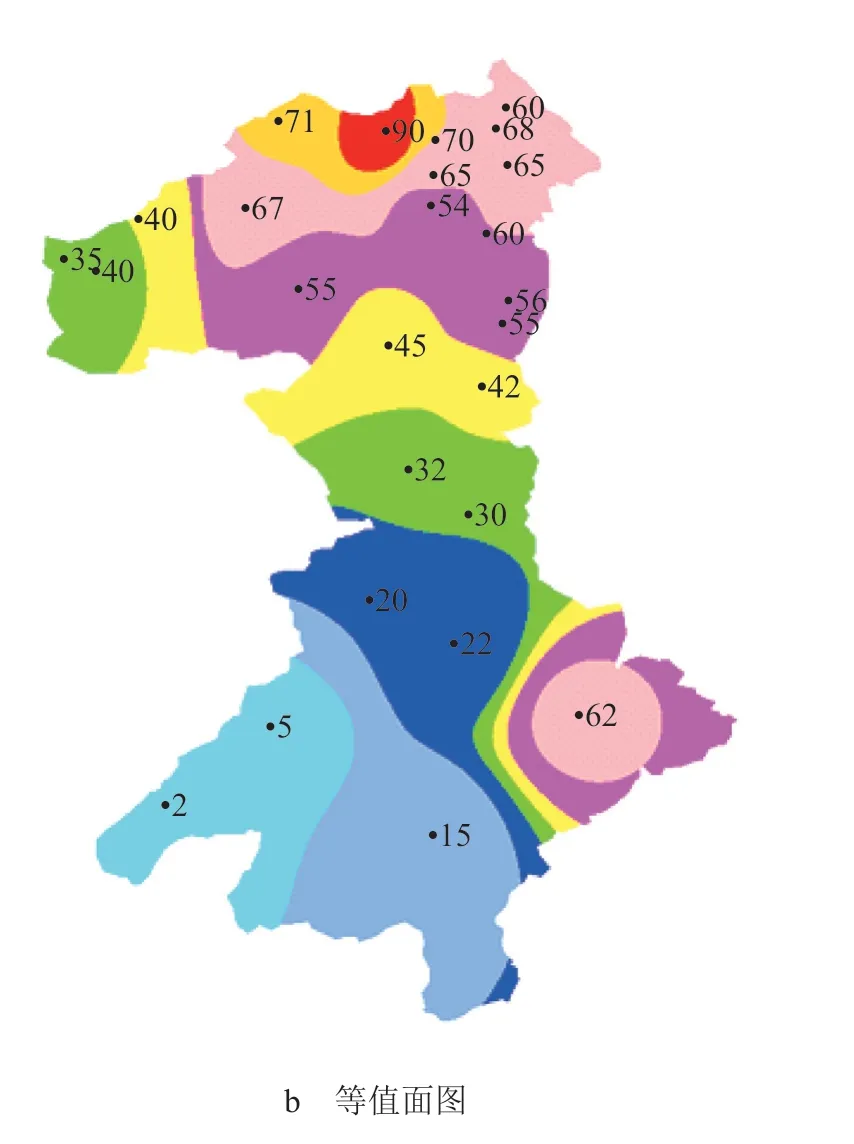
图7 等值线生成结果
网格规模为 1 000×1 000,站点数量为 26 个的等值线生成计算表明,等值线生成计算所需时间约为 3 s,在计算效率上能够满足实际业务的需要。任意改变站点的数量和雨量值,该等值线算法组件均能正常生成雨量等值线,表现出较好的算法健壮性。该算法组件在全国 200 多个县级山洪灾害监测预警系统中,以及多个省、市级水资源监测管理和中小河流监测预报预警等系统中得到应用,表现出良好的站点数据适应能力,并能够较好地表达降雨、水资源的空间分布信息,满足水利信息化相关应用需求。
3 结语
基于网格延展法生成等值线算法利用研究区域内网格分布的特性,在计算范围的确定、等值面的提取上提供了一种新的方法,避免基于等值线追踪时出现交叉、分叉等复杂问题,避免了等值线生成结果的裁剪计算。网格延展法生成等值线在重分类时,可以根据生产应用需要,生成不同空间梯度的等值线。实际应用表明,网格延展法生成等值线算法对不同的研究区域边界、测站的数据具有较好的适应性,算法表现为良好的健壮性。基于网格延展法生成等值线算法简单,可使用多种语言实现,能与多数的水利信息化应用系统进行集成。但本研究生成的雨量等值线图(如图7 b)只能表达不同雨强分布区域的分界线,不能表达相同数值点构成的等值线,在这一方面基于网格延展法生成等值线尚需进一步研究和改进。

