移动分析法在中长期水位预测应用中的研究

韦广龙 ，黎协锐 ，李必元

（1. 广西南宁市水文水资源局南宁水文站，广西 南宁 530008；2. 广西财经学院，广西 南宁 530003；3. 广西南宁市水文水资源局，广西 南宁 530001）

0 引言

洪涝灾害是当今我国最主要的自然灾害之一，已成为影响和制约我国经济社会可持续发展的一个重要因素，防洪减灾的任务艰巨而迫切。而做好防洪减灾工作，洪水的预报预警在防洪策略中占有重要地位。

在多年的科研和实际防汛工作中，我国的洪水预报在基础理论、技术方法和实际经验上取得了巨大成绩，特别是“98 特大洪水”以后，洪水预报在预报方法、系统建设、作业管理及新技术应用等方面有了新的进展[1]。目前，比较成熟且应用比较广泛的洪水预报方法是基于大气环流、海洋潮汐、各种地球物理因子和下垫面产流汇流条件等物理成因分析基础上的经验方法，如新安江、马斯京根模型等短期预报方法[2]。中长期水文预报与天气气候、气象预报紧密关联，而影响长期天气过程变化的成因极为复杂，且受各种不确定因子的制约，还与适用的数理统计方法或大数据分析理论有关，是国内外尚属探索中的课题[3]。

国内在中长期水文预报方法的研究方面有许多文献，如：汤成友等的《现代中长期水文预报方法述及其应用》[4]，李崇浩等的《水文周期迭加预报模型的改进及应用》[5]，许定雄的《关于中长期水文预报方法的研究》[6]。有些文献中利用方差分析周期外推方法，提出了改进的正规化周期回归模型，即利用非线性回归消除模型的趋势项，利用正规化方程组进行方差分析，完成对周期项的识别提取，进而利用趋势项与周期项进行模拟和预测[7-8]。中长期水位预测主要有方差分析法、平稳时序法、逐步回归法、多因子分析法等方法，这些方法只能做出 1 个水位预测方案，同一种方法没有用多个水位预测方案对比，由于没有可比性，也就失去实用性。因此，探索一种能做出多个水位预测方案，既有高的预测精度，又有实用价值，且可信息化的中长期水位预测方法，即采用移动步长法和方差分析法进行组合研究，以优选分析方式形成移动分析法，获取年最高水位预测最佳方案，再计算中长期水位预测值。

1 方法创建

采用移动步长法把原年最高水位系列分成十几到几十个分系列，通过方差分析法计算得到年最高水位预测方案，经过优选对比法优选方案，以优选率高的方案作为年最高水位预测最佳方案，再以年最高水位预测最佳方案计算得到中长期水位预测值，由此创建移动分析法。移动分析法是在方差分析法的基础上改进的，加入移动步长法和优选对比法组合一体化的中长期水位预测方法。

移动分析法采用电脑编程应用软件将原数据系列录入，首先用移动步长法分成多组数据系列，然后用方差分析法计算模块分别对各组数据系列进行计算，得到相应数据系列的预测方案，再用优选率模块进行各预测方案的合格率、准确率计算得到优选率，以优选率进行方案优选，采用优中选优，从各分组数据系列优选方案排列第 1～5 预测值，取5 个预测值的平均值为采用预测值。

1.1 基本概念

移动步长法是对某一事件已出现的数值系列，用设定的步长移动，按原序号建立相应的数值系列N 的方法。

方差分析法又称“F 检验”，是对试验数据进行分析，检验方差相等的多个正态总体均值是否相等，进而判断各因素对试验指标的影响是否显著的方法[9-10]，本研究是用于评价总变动性来自每一变动源中各分组显著性的一项技术。根据影响试验指标条件的个数可以区分为单因素、双因素和多因素等方差分析。移动分析法采用单因素方差分析。

1.2 基本依据

1.2.1 移动步长法

移动步长法的表达式为

式中：L 为移动步长；y 为移动步长递增数，y = n +1（n = 0，1，2，3，4，5）。

1.2.2 方差分析法

方差分析的基本原理是认为不同处理组的均值间的差别基本来源有以下 2 个：

1）实验条件。不同的处理造成的差异，称为组间差异，用变量在各组的均值与总均值之偏差平方和的总和表示，称为组间平方和，记为 SA，组间自由度记为 d1。

2）随机误差。测量误差造成个体间的差异，称为组内差异，用变量在各组的均值与该组内变量值之偏差平方和的总和表示，称为组内平方和，记为SE，组内自由度记为 d2。

则总偏差平方和 ST= SA+ SE。

SA，SE除以各自的自由度（d1= k - 1，d2= n -k，其中 n 为样本总数，k 为组数），得到组间均方 SA和组内均方关系有 2 种情况：一种情况是处理没有作用，即各组样本均来自同一总体，≈ 1；另一种情况是处理确实有作用，组间均方是由于误差与不同处理共同导致的结果，即各样本来自不同总体，那么，（远远大于）。

相关公式主要有以下 2 种：

1）平均数公式。公式为

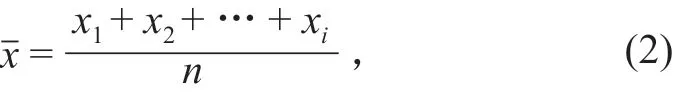
2）方差公式。公式为

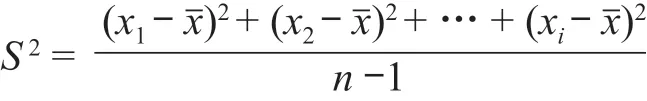
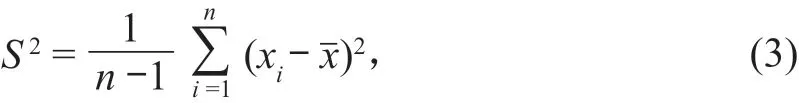
或式中：S 表示这组数据的均方差。

1.2.3 方差分析的改进

由方差分析改进得周期迭加预报，周期迭加预报是中长期水文预报的一种实用模型[11]。针对该模型中用方差分析法无法处理而舍弃的最终残余系列，提出最终余波概念及相应的分析方法，实现对最终余波的信息挖掘利用[12-13]。

一般而论，一个水文要素序列 X (t) 包含有趋势成份 Pi(t)、周期成份 C (t)、相依成份 n (t) 和独立随机成份 ε (t)。具体计算公式如下：

式中：Pi(t) 为第 i 周期波；ε (t) 为误差项；l 是 X (t)的 i = 1，2，3，…，n 中，n 的代用字母，l = n。

1.3 F 检验

本研究在对西江流域南宁、崇左、龙州等水文站历年年最高水位系列进行周期显著性普查时，采用 F 检验。要分析南宁水文站历年年最高水位序列的周期，就是要分析其中的周期成份 C (t) 项[14]。具体计算公式如下：

K 表示第 i 组的项数。

2 预测方案建立

2.1 方案条件

移动分析预测方案建立主要满足以下 2 个条件：

1）数据系列满足 N ≥ 20 个样本。技术要求每个方案大于等于 20 a 系列，以达到中长期水位预报的数据系列代表性。

2）移动步长数为 2 ≤ L ≤ 10。技术要求数据系列满足建立 10 个以上的预测方案，目的是通过优选方案，提高方案的合格率和准确率。方法是用不同的移动步长进行试算后，选择优选移动步长数范围。本方案设定最大移动步长数 L = 10，做 10 个方案，并需包括大、平、小水年。因此，每个方案大于等于 20 a 系列。

设定依据如下：根据 GB/T 22482—2008《水文情报预报规范》规定，编制预报方案所引用的水文资料，应有足够的代表性，一般不得少于 10 a 系列，并需包括大、平、小水年[15]1。

2.2 关键技术

2.2.1 分组数据系列计算

采用移动步长法，对原数据系列 N 进行计算，计算公式如下：

式中：hi为新系列开始数；m 为原始数据系列开始数；Li为移动步长数（i = 1，2，…，9）；pi为新系列序号。

以南宁水文站 1936—2017 年年最高水位系列为例，按式 (8) 分别进行移动步长数（Li= 2，3，4，5，6）分系列计算，结果如表1 所示。

表1 南宁水文站 1936—2017 年年最高水位系列移动步长数 2～6 系列计算表

由表1 计算得到，南宁水文站 1936—2017 年年最高水位系列移动步长数 Li= 2，3，4，5，6 分系列，分别是 32，21，16，13，11 个计算方案，根据中长期水文预报方案的要求，设定参与方案分析计算的数据为 20 个以上，确保方案的代表性和可信度。假设某个站从 1981 年起有实测数据，则系列为1981—2017 年，共 37 a，采用移动步长数 L = 8，只有 1981—2017 年，1989—2017 年，1997—2017 年3 个方案，3 个方案难于作方案优选，不能提高预报方案的合格率和准确率。南宁水文站 1936—2017 年年最高水位系列的分系列预报方案在 10 个以上，每个方案均在 20 a 系列以上。

以南宁水文站 1936—2017 年最高水位系列，移动步长数 L1= 2 分系列进行计算，共计算得 32 个方案，具体如表2 所示。

由表2 可得，Pi为新系列序号，南宁水文站1936—2017 年年最高水位系列移动步长数 L1= 2 分系列 hi，共 32 个系列方案，每个方案均在 20 a 系列以上。

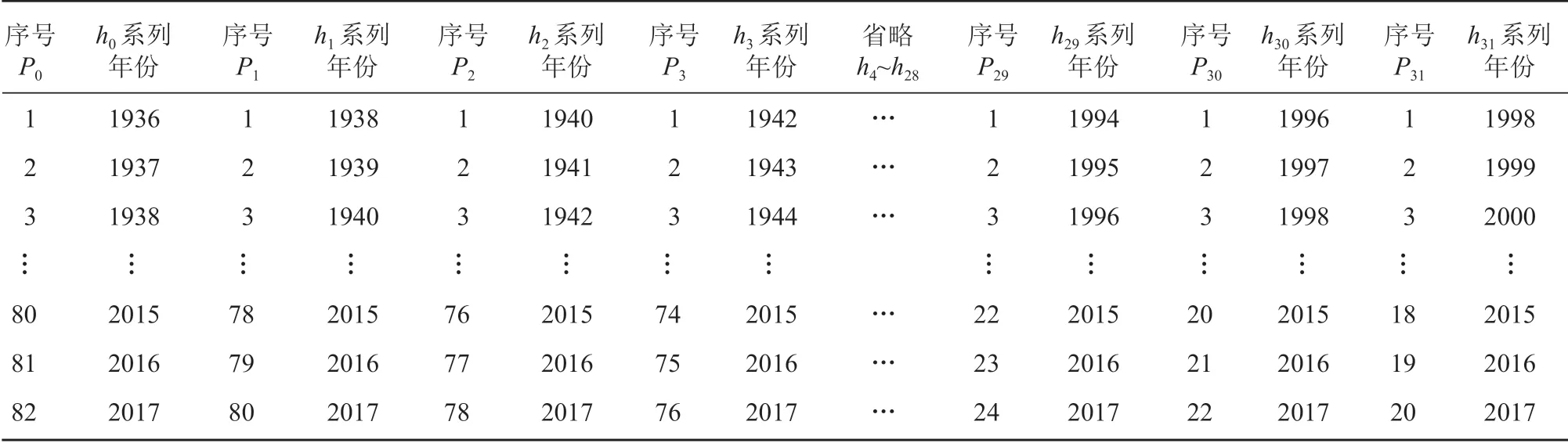
表2 南宁水文站 1936—2017 年最高水位系列移动步长数 L1 = 2 系列计算表

采用方差分析法对南宁水文站 1936—2017 年年最高水位系列移动步长数 L1= 2，P = 27 的分系列进行预报。分系列 h30= 1 936 + 2×27 = 1 990，即分系列为 1990—2017 年年最高水位系列，计算结果如表3 所示。

从表3 可得，1990—2017 年实测水位变幅 ΔZ =77.94 - 67.42 = 10.52 m，根据 GB/T 22482—2008《水文情报预报规范》，水位预报以实测变幅的 20%作为许可误差，则许可误差 = 20%×10.52 = 2.10 m。一次预报的绝对误差的绝对值小于等于允许误差为合格，否则为不合格，因此南宁水文站 1990—2017 年年最高水位方案合格率为 100%。2017 年年最高水位预报值为 70.47 m，实测值为 70.44 m，δ 为绝对误差的绝对值，则准确率 kz=（1 - δ/ΔZ）×100% =[1-（70.47 - 70.44）/10.52]×100% = 99.7%。

表3 中的 1，2，3 周期值计算方法，用 F 检验公式对南宁水文站 1990—2017 年（28 a）年最高水位序列 X (n) 进行周期普查，依次按 2，3，…，n/2进行排列，分别计算 F 值，再从 2～n/2 中选取 F 值最大那个年，作为第 1 周期，同时组成 1 个序列。其次，将原序列减去该序列得到残余序列，再重新上述步骤，普查 3 个周期。经计算得：第 1 周期 l1=10，F1= 2.708；第 2 周期 l2= 9，F2= 3.421；第 3 周期 l3= 12，F3= 3.783。由此可知，F ＞0.5，则序列显著存在周期。

对南宁水文站各移动步长 L = 3～6 系列的方差分析预测计算，因计算方法相同，在此不列出。按照南宁水文站的计算方法，分别对崇左、龙州水文站各移动步长 L = 2～6 系列的方差分析预测计算，分析预测计算成果表在此不列出。

表3 南宁水文站 1990—2017 年年最高水位方差分析法预测计算表

2.2.2 优选率计算

移动分析法采用优选方式选出最佳预测方案、最优预测值，因此，移动分析法以水位预测方案平均合格率和预测值的准确率计算优选率。计算公式为

式中：Kc为方案优选率；Kv为方案合格率；a 为合格率的优选率加权数，a＝0.5～1.0；b 为准确率的优选率加权数，b ＝ 0.1～0.5。

按式 (9)，优选率 Kc为 Kv和 Kz的算术平均值，即= 0.5 Kv+ 0.5 Kz，优选率加权数a 和 b 都是相等的，即 a + b = 0.5 + 0.5 = 1.0。

根据移动分析法以提高预测方案合格率为目的，为区分多个合格率相同（合格率 100%）的方案，在第 1 选项合格率之后，加入第 2 选项系列尾数预测值的准确率作为评估参数，将 Kv和 Kz分别乘以优选率加权数 a，b，计算得到 Kc。本案例水位预测方案 Kv为主要份量，a 取值大于 0.5，b 取值小于 0.5，则选用方案 Kc计算比值系数为 0.6∶0.4 和0.7∶0.3。

分别计算 0.6∶0.4 和 0.7∶0.3 的平均优选率Kc，并进行比较，以 Kc大的作为优选比值系数。

2.2.3 预测值计算

采用方差分析法计算得到各分组数据系列优选方案的预测值，从各分组数据系列第 2～6 移动步长年方案各选 1 个优选率最高、排序第一的方案预测值，计算 5 个预测值的平均值为年最高水位预测值。

3 应用案例分析

以南宁、崇左、龙州 3 个水文站的年最高水位系列年为例，年最高水位系列年分别是 1936—2017 年，1954—2017 年，1946—2017 年，将年最高水位系列年按式 (8) 计算重组系列，采用方差分析法根据 3 个水文站年最高水位系列计算各个方案的合格率和准确率。

在同样条件下，采用移动分析法分别建立南宁、崇左、龙州水文站年最高水位预测方案，采用移动步长法分别计算第 2～6 移动步长年年最高水位分系列，采用方差分析法（采用第 1～3 周期）计算第 2～6 移动步长年年最高水位分系列预测值，从而建立各分系列预测方案，根据最优预测方案计算2018 年年最高水位预测值。

3.1 计算优选率

根据南宁（1936—2017 年）、崇左（1954—2017 年）、龙州（1946—2017 年）3 个水文站年最高水位数据系列，采用移动分析法计算，按优选方案分别计算第 2～6 移动步长年的水位预测值。南宁、崇左、龙州 3 个水文站的水位变幅分别为 ΔZ1，ΔZ2，ΔZ3，计算如下：ΔZ1= 77.94 - 67.42 = 10.52 m（2001—2007 年），允许误差 = 10.52 × 20% =2.10 m；ΔZ2=107.66 - 92.57 = 15.09 m（1987—2008 年），允许误差 = 15.09 × 20% = 3.02 m；ΔZ3=126.09 - 111.25 = 14.84 m（1976—1986 年），允许误差 = 14.84 × 20% = 2.97 m。

南宁水文站采用移动分析法预测 2017 年年最高水位，优选方案比值系数计算如表4 所示。

根据表4 中南宁水文站 2017 年年最高水位系列移动步长数 L = 2，P = 32 所得的成果，可分别得出移动步长数 L = 2～6 的方案计算成果。

表4 中，从排列 1～5 的优选率 Kc比较可知，按 0.6∶0.4 计算得出的优选率 Kc比按 0.7∶0.3 计算得出的 Kc小，则计算得出的平均优选率也比按0.7∶0.3 计算得出的值小，因此方案采用 0.7∶0.3计算优选率 Kc。

按照南宁水文站的计算步骤，分别对崇左、龙州水文站各移动步长 L = 2～6 的系列进行优选得到5 个优选率排在第 1～5 名的系列方案，由于计算方法与南宁水文站相同，故成果在此不列出。

3.2 确定优选方案

南宁水文站采用移动分析法预测 1936—2017 年年最高水位，其中 1990—2017 年方案优选率最高，Kc= 99.9%，排序第一，则选为最优方案。

崇左水文站采用移动预测法预测 1954—2017 年年最高水位，其中 1993—2017 年方案优选率最高，Kc= 98.4%，排序第一，则选为最优方案。

龙州水文站采用移动预测法预测 1946—2017 年年最高水位，其中 1996—2017 年方案优选率最高，Kc= 99.1%，排序第一，则选为最优方案。

南宁、崇左、龙州水文站采用移动分析法预测年最高水位优选方案统计表如表5 所示。

由表5 可知，南宁、崇左、龙州水文站采用移动分析法计算年最高水位时，按 0.7∶0.3 计算得出的 Kc最高。

4 优选年最高水位预测值计算

从优选南宁、崇左、龙州水文站第 2～6 移动步长年方案各选 1 个优选率最高，排序第一的方案，取 5 个方案水位预测值的平均值作为水位预测值，计算结果如表6～8 所示。

表4 南宁水文站采用移动分析法优选方案 Kc 比值系数计算表

表5 南宁、崇左、龙州水文站采用移动分析法预测年最高水位优选方案统计表

表6 南宁水文站采用移动分析法作 2018 年年最高水位优选预测方案计算表

表7 崇左水文站采用移动分析法作 2018 年年最高水位优选预测方案计算表

表8 龙州水文站采用移动分析法作 2018 年年最高水位优选预测方案计算表

由表6～8 可知，南宁、崇左、龙州水文站采用移动分析法计算得到 2018 年年最高水位，年最高水位预测值分别为 72.66，97.78，114.84 m。

5 预测方案评估

移动分析法在南宁、崇左、龙州 3 个水文站中长期水位预测预报应用，最突出的优点是能提供多套水位预测方案优选，经优选后得出最佳预测方案，并且预测精度高。

5.1 预测年最高水位

采用移动分析法进行南宁、崇左、龙州 3 个水文站 2018 年年最高水位的预测，由表6～8 可得年最高水位，最高水位精度统计表如表9 所示。

根据 GB/T 22482—2008《水文情报预报规范》，预测值准确率大于等于 80.0% 为合格，否则即为不合格[15]5。由表9 可得，南宁、崇左、龙州水文站年最高水位优选方案预测值准确率均大于 80.0%，为合格。

南宁、崇左、龙州 3 个水文站采用方差法预测2018 年实测年最高水位统计表，如表10 所示。

由表10 可知，南宁水文站单站应用预测值准确率为 61.3%，为不合格；崇左、龙州水文站单站应用预测值准确率分别是 86.6%，96.2%，为合格；总体应用预测值平均准确率为 81.4%，为合格。

5.2 实测年最高水位

根据南宁、崇左、龙州水文站 2018 年实测水位成果得到 2018 年年最高水位，如表11 所示。

由表11 可知，南宁、崇左、龙州水文站 2018 年实测年最高水位分别为 72.28，98.77，115.25 m。

对移动分析法与方差分析法进行对比分析。从表9 与 11 对比分析可知，南宁、崇左、龙州水文站 2018 年移动分析法平均合格率和准确率分别为99.5%，95.6%，方差分析法平均合格率和准确率分别为 77.3%，81.4%，移动分析法比方差分析法的年最高水位预测合格率和准确率分别高 22.2% 和14.2%。应用结果表明，移动分析法作为改进后的方法更好地利用水文因子，提高了水位预报的精度。

6 结语

在对南宁、崇左、龙州 3 个水文站年最高水位进行预测时，各系列方案的合格率有高有低，有不合格，这是中长期水位预测的常见性和必然性，是中长期水位预测的普遍性。在方差分析法基础上加入移动步长法的移动分析法，是一种改进分析法。移动分析法在中长期水位预测应用过程中，存在诸多的合格率 100% 方案不相同的水位预测值，通过加入预测年的准确率计算优选率，以优选率高优选预测方案，预测精度高。目前研究范围只有中长期水位预测，尚未对中长期流量、洪量、径流量的预测进行分析，如果进行这些研究可能会有较多的问题需要创新方法来解决。

表9 南宁、崇左、龙州水文站采用移动分析法预测 2018 年年最高水位精度统计表

表10 南宁、崇左、龙州水文站采用方差分析法预测 2018 年年最高水位统计表

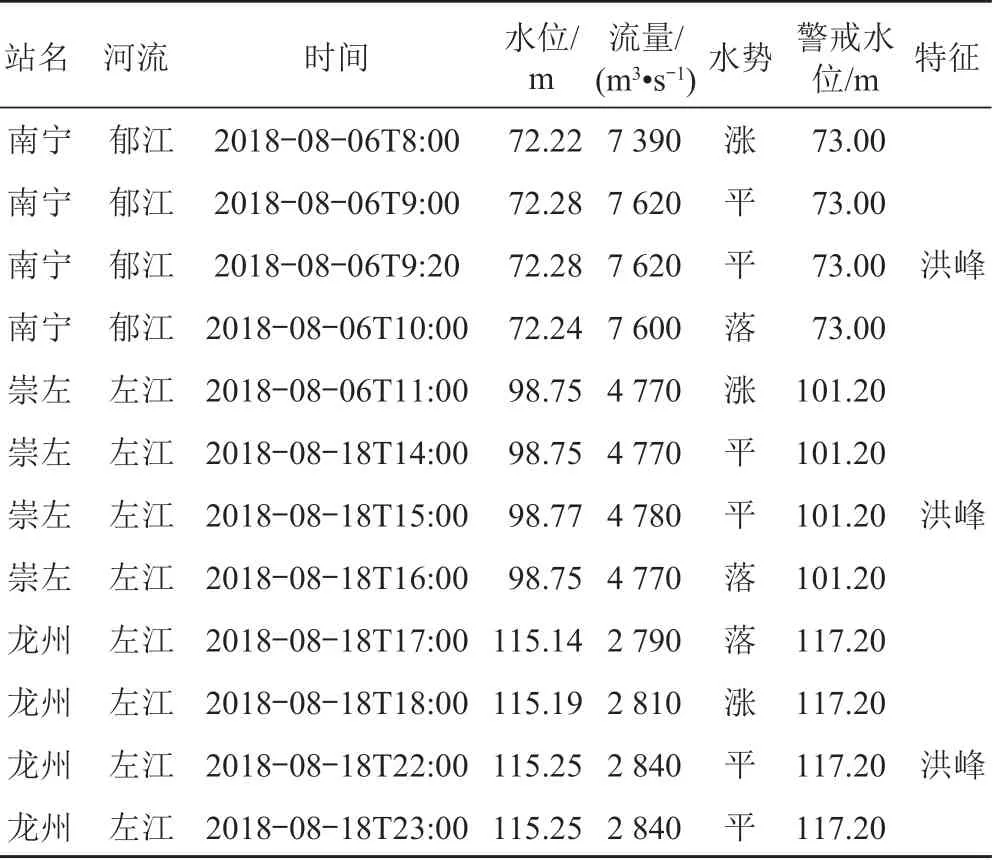
表11 南宁、崇左、龙州水文站 2018 年实测年最高水位表

移动分析法在中长期水位预测应用中的研究理论上是一种方法的创新，应用价值比较大，比较适合作中长期水位预测方案，预测精度高，预见期长，可发挥预测预警水位信息的耳目作用，在经济社会建设、防灾减灾、防汛调度方面做出新贡献。建议今后应深入移动分析法研究，建立移动分析法的中长期水位预测预警系统，推进水文预测预警信息化建设，实现水位预警信息智能化，更好地防灾减灾服务。