多端柔性直流输电直流电压控制策略研究

唐 震

（国网山西省电力公司电力科学研究院，山西 太原 030001）

0 引言

电压源换流器高压直流输电VSC-HVDC（voltage source converter based high-voltage direct current transmission） 系统能够实现有功功率和无功功率的独立控制，具有占地面积小、不需要无功补偿、不存在换相失败以及可以向无源系统供电等诸多优点，在特高压/高压远距离输电、背靠背联网、分布式电源系统并网以及构建城乡直流配电网等领域具有广泛的应用前景，也是目前工程领域与学术领域的研究热点[1-3]。电压源换流器的直流输电系统在系统潮流反转时，可以保持直流电压极性不变，这种特性使得电压源换流器在构建多端柔性直流输电系统时变得更加方便[4-5]。国内浙江舟山海岛供电工程、广东汕头南澳接入示范工程和张北柔性直流工程等多个多端柔性直流输电工程VSCMTDC（voltage source converter based multi-terminal HVDC） 在近几年已投入商业运行[6-7]。

VSC-MTDC 直流输电系统由3 个及以上的换流站以及输电线路构成，站间控制复杂程度大大提高，如何实现系统内多换流站之间的协调和控制是系统能否稳定运行的关键环节，系统直流电压保持在给定的运行区间内则是系统稳定运行的必要条件[8-12]。文献[13] 提出了适用于多端柔性直流输电的直流电压斜率控制，即在不依赖于站间通信，保持系统直流电压稳定的前提下，不平衡功率依据每个换流站给定的功率与电压曲线来分配。文献[14]提出了斜率控制和直流电压偏差控制相结合的优化控制策略，但在控制模式切换时该策略会造成系统的附加扰动。文献[15] 在考虑了换流站直流功率调节上限的基础上，对直流电压斜率控制策略进行了修正，最终提出了一种能够使系统合理分配不平衡功率的自适应斜率控制策略，但该策略没有考虑系统故障后的恢复，而且需要频繁切换控制器。文献[16] 提出了将稳定直流电压的任务分配给多个换流站的直流电压斜率控制策略，为实现系统功率平衡和分配，运行在该策略下的换流站沿着各自独立的特性曲线寻找新的运行点。但是该策略并未考虑各换流站的实际负载情况，若按照固定斜率承担系统的不平衡功率，对于容量裕度有限的换流站，可能会导致满载，进而切换为定有功功率控制，这样将失去对系统潮流变化的响应能力。

本文提出一种考虑换流站容量裕度和功率调节速度的直流电压的自适应控制策略，旨在修正直流电压斜率控制策略的不足，并进行了仿真分析。结果表明，该控制策略无需换流站间通信，能够保证系统不平衡功率在各换流站的合理分配，与直流电压固定斜率控制相比能有效维持系统的稳定运行。

1 VSC-MTDC 系统

VSC-MTDC有多种拓扑结构，但已投运的工程大多采用可控性能好、扩展性强的多端并联结构。对于直流输电线路而言，由于没有电抗且电阻较小，因此并联系统中各节点的电压接近相等。为了保证系统潮流的平衡，在多端系统中必须至少有一端换流站采用定直流电压控制，其余换流站采用定有功功率控制。本文仅以四端两电平柔性直流输电系统为例开展分析研究，其系统如图1 所示。四端系统中，VSC1 和VCS2 为整流站，工作于直流电压自适应斜率控制模式；VSC3 与VSC4 为逆变站，工作于定有功功率模式，系统不考虑换流站功率返送运行模式。换流站交流侧与交流等值系统相连；T1、T2、T3、T4为换流变压器。

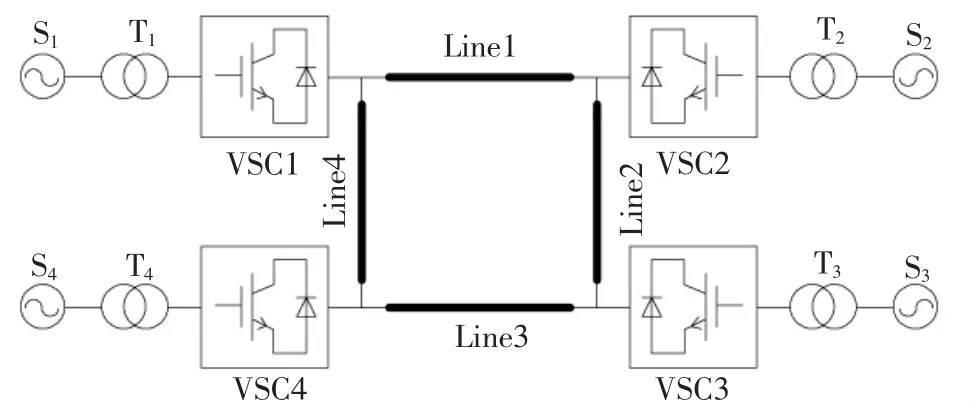
图1 并联结构的四端柔性直流输电系统图

四端系统中各换流站功率方向以交流系统注入换流站为参考正方向。系统中4 个换流站的结构完全一样，其物理模型如图2 所示。图2 中，Us为交流电网电压，Uc为换流站输出电压的基频分量，δ 为换流站交流侧电压基波相位超前交流侧系统电压相位的角度，R、L为变压器和电抗器的等效电阻、电感，Pc为换流站有功功率，Ps为交流电网的有功功率，Udc为直流侧正负极电压，Idc为直流输电线路电流，Pdc为直流功率。

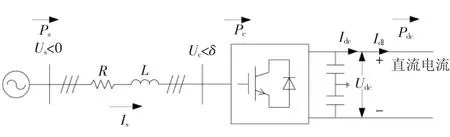
图2 换流站的稳态物理模型

当只考虑输出电压的基波分量，根据图2 列出的交流侧矢量方程为

将式（1） 转换到dq旋转坐标系下，换流站的数学模型为

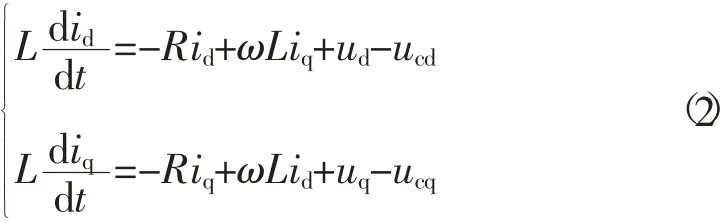
式中：下标d、q 分别表示电压、电流转换到dq坐标系下的d、q轴分量；ω 为电网基波相量的角频率。

由式（2） 可知，在引入耦合项ωLid、ωLiq后，使得d、q轴电流解耦和系统功率控制解耦，在提高系统稳定性的同时也实现了快速功率响应。再引入ud、uq前馈项后便可构成内环电流解耦控制器。

在dq坐标系下，换流器交流侧有功功率、无功功率可表示为

当电网三相对称，电压矢量选取为d轴方向时，usq=0，usd=Us。忽略电抗器和换流器损耗时，换流站交直流两侧的有功功率相等，即

式中：Pdc和Idc分别为直流侧功率和电流。

由式（4） 可知，当换流站交流侧有功功率与直流侧功率不相等时，为了平衡系统功率，直流电容将会进行充、放电，从而导致系统直流电压上升、下降，直流电压最终会达到一个新的稳定值。若功率差额较大时，直流电压将有可能失去控制，导致系统失去稳定。因此，定直流电压控制的换流站可以认为是一个有限容量的系统功率平衡节点。

2 VSC1 换流站直流电压控制

在多端柔性直流输电系统中，必须有一个换流站采用定直流电压控制，为此首先对单点直流电压控制进行仿真研究。

直流侧电容值取C=600 μF；各换流站之间电缆长度均为5 km。4 个换流站的参数和控制方式见表1。

表1 4 个换流站参数表

四端系统中换流站1 采用定直流电压控制，2、3、4 换流站均采用定有功功率控制。功率指向均以交流系统流向换流站为正。0～3.0 s 时换流站1无功指令为Q1=0.3 Mvar；换流站2 有功指令为P2=0.7 MW；换流站3 有功指令为P3=-1.0 MW、Q1=0.3 var；换流站4 有功指令为P4=-0.5 MW。3.0 s时刻换流站3 有功功率由-1.0 MW 改变为-1.8 MW，5.0 s 返回原值。仿真结果见图3。

在图3 中，Vdc1～Vdc4表示4 个换流站的直流电压；P1～P4表示4 个换流站的有功功率（以下相同）。从图3 可以看出，在3.0 s 时刻换流站3 发生-1.0～-1.8 MW 的有功功率指令变化时，整个系统的功率缺额全部由主导站——定直流电压控制的换流站1 来承担，其他换流站并不参与调节，如果这个换流站因事故或满载切换为定功率模式失去了直流电压的控制能力，整个系统将失去稳定。由此可以看出，单个换流站采用直流电压控制时整个系统的可靠性较差。因此，有文献提出适用于VSCMTDC 系统的多换流站直流电压偏差控制策略，其实是在主导换流站失去直流电压控制能力时，备用换流站在直流电压偏差过大时转为定直流电压控制，以维持直流电压达到稳定整个系统的目的。其不足之处在于对直流潮流变化的响应速度不够快速且容易导致该换流站过载。

3 多点直流电压自适应斜率控制

直流电压斜率控制是系统内多个换流站根据直流电压值按固定斜率调整其功率指令参考值，能够快速地实现系统功率平衡和站间分配的策略。直流电压斜率控制器见图4。图4 中，Ps，ref为有功功率指令值，Ps为换流站运行功率值，Udc为直流电压值，Udc，ref为直流电压指令值，K为换流站的直流电压斜率控制系数。由图4 可知，直流电压与功率之间的关系为

图3 换流站3 有功改变时各换流站电压和功率

图4 直流电压斜率控制器

其中，K为直流电压斜率控制系数，可由式（6） 计算得出

为保证直流电压斜率控制曲线在电压波动的限值以内，要求0＜β≤1。这里取β=0.75。

由式（5）、式（6） 可知，在平衡直流系统功率时直流电压斜率控制策略并没有考虑每个换流站的容量裕度，因而容易导致直流电压斜率控制的换流站满载从而切换为定有功功率模式。

本文针对直流电压斜率控制策略的不足，提出了考虑换流站功率裕度的多点直流电压自适应斜率控制策略。该控制策略无需站间通信，一方面保证了功率在柔性直流输电系统合理分配，避免了换流站因满载运行切换为定功率运行的情况；另一方面增加了一个系统平衡点，因而保证了整个系统的稳定运行。

一种考虑换流站容量裕度的直流电压自适应斜率控制策略，其基本思想是基于换流站容量裕度和调节速度的关系来修正式（5） 中斜率K值。一般而言，换流站运行时容量裕度η 越大，其调节速度v可以越大，即希望K值越小；相反，当容量裕度η 越小，则希望其调节速度越小，K值越大。也就是说可以利用v和η 构造一个函数来修正斜率系数K。

这里我们通过η（0.9%，0.8%，0.7%，0.6%，0.5%，0.4%，0.3%，0.2%，0.1%） 和v（10，10，5，2.5，2，1.667，1.25，1.0，1.0） 构建一个函数f（η），其中η 的取值范围为0.1≤η≤0.9。

利用f（η） 来修正斜率系数K，即K*=K×f（η）。基于K*建立的控制器结构如图5 所示。

图5 中，Ps，ref为有功功率指令值，Ps为换流站运行功率值，Udc为直流电压值，Udc，ref为直流电压指令值，K*为换流站的直流电压自适应斜率控制系数。

图5 直流电压自适应斜率控制器

4 仿真分析

为验证本文所提控制策略的有效性，利用表1参数所建立的四端柔性直流输电系统进行仿真验证。仿真中，换流站1和换流站3 额定容量都为3 MW，换流站2 和换流站4 额定容量都为1 MW。其中换流站1 与换流站2 采用定直流电压自适应斜率控制，换流站3 与换流站4 采用定有功功率控制。换流站1和换流站3 与10 kV 交流等值系统相联，换流站2与换流站4 与0.38 kV 交流等值系统相联。这里换流站1、换流站2 取7.5%作为直流电压波动极限值，按照式（6） 可以计算出固定斜率系数分别为0.225、0.675。

算例1：换流站1～换流站4 的有功功率指令值分别为0.8 MW、0.7 MW、-1.0 MW、-0.5 MW。图6 给出了本文提出的自适应斜率控制与固定斜率控制的仿真结果和对比情况。图6 中，数字1、2表示换流站；z、g 分别表示自适应和固定斜率控制模式；Vdc、P分别表示直流电压和有功功率模式，以下相同。

由图6 可以看出，自适应直流电压斜率和固定斜率控制在正常运行时基本相同，能够很好地满足系统运行要求。

算例2：初始状态下，换流站1～换流站4 有功指令分别为0.8 MW、0.7 MW、-1.0 MW、-0.5 MW。在3.0 s 时刻，换流站3 有功功率由-1.0 MW 改变为-2.0 MW，5.0 s 返回原值。仿真结果见图7。

由图7 可以看出，自适应斜率（实线） 与固定斜率（虚线） 两种控制模式直流电压与有功功率变化趋势相同，自适应斜率控制直流电压降低幅度较小，而容量裕度更大的换流站1 承担的有功功率更多，能够更好地限制换流站2 的过载。

图6 两种直流电压控制比对

图7 换流站3 功率改变时两种控制比对

对于自适应斜率控制策略：在3.0 s 时刻换流站3 功率指令改变后，直流系统出现功率不足，直流电压Udc由12 kV 降低至11.5 kV，换流站2 因容量裕度较小，承担有功功率缺额较小，为0.173 MW；换流站1 由于容量裕度充足，承担系统有功功率缺额较大，为0.85 MW，使换流站2不会过载，系统运行工况得到了优化。

对于固定斜率控制策略：换流站1 和换流站2可以根据其直流电压的数值按固定斜率0.225 和0.675 调整其传输的功率。在3.0 s 时刻换流站3功率指令变化后，整个直流系统出现功率缺额，直流正负极电压Udc由12 kV 降低至11.3 kV，换流站2 承担有功功率缺额0.23 MW，换流站1 承担系统有功功率缺额0.7 MW。

由以上分析可知，自适应斜率控制从容量裕度角度考虑各换流站功率分配量，在直流系统出现功率缺额时，能够使功率裕度较大的换流站承担更多的功率缺额。

算例3：初始状态下，换流站1～换流站4 有功指令分别为0.8 MW、0.7 MW、-1.0 MW、-0.5 MW。在3.0 s 时刻，换流站4 的功率指令由-0.5 MW 变化为-0.1 MW。图8～图10 给出了两种控制方式的仿真对比结果。

由图8～图10 可以看出，3.0 s 时刻换流站4功率指令变化后，直流系统出现剩余功率，直流电压逐渐升高，但明显地固定斜率控制直流电压上升更多，也意味着其调节速度偏慢。虽然两种斜率控制均能满足直流系统功率的平衡，但在3.0～5.0 s 期间由于换流站1 的功率裕度较大，K1z

算例4：初始状态下，换流站1～换流站4 有功指令分别为0.8 MW、0.7 MW、-1.0 MW、-0.5 MW。在3.0 s 时刻，Line1 末端（换流站2 侧） 发生正极接地故障，仿真结果见图11～图13。

图8 换流站1、换流站2 直流电压对比

图9 换流站1、换流站2 有功功率对比

图10 换流站1、换流站2 斜率系数对比

3.0 s 时刻Line1 末端发生正极接地，自适应斜率控制模式时换流站1、换流站2 侧直流电压最高为13.84 kV、13.82 kV，最低为4.46 kV、5.91 kV。换流站1、换流站2 侧有功功率最高为2.25 MW、1.94 MW，最低为0.16 MW、0.3 MW。

固定斜率控制模式时换流站1、换流站2 侧直流电压最高为13.77 kV、13.73 kV，最低为4.45 kV、5.88 kV。换流站1、换流站2 侧有功功率最高为2.18 MW、1.94 MW，最低为0.18 MW、0.38 MW。

从上述结果可以看出，两种斜率控制仿真结果差距不大，控制效果基本相同。

算例5：初始状态下，换流站1～换流站4 有功指令分别为0.8 MW、0.7 MW、-1.0 MW、-0.5 MW。在3.0 s 时在S2 侧发生交流三相接地故障，故障时间0.15 s，5.0 s 闭锁换流站2，仿真结果见图14～图16。

图11 两种斜率控制换流站1、换流站2 直流电压

图12 两种斜率控制换流站1、换流站2 有功功率

图13 换流站1、换流站2 两种斜率

图14 两种斜率控制换流站1、换流站2 直流电压

图15 两种斜率控制换流站1、换流站2 有功功率

图16 换流站1、换流站2 两种斜率

由图14～图16 的仿真结果可知，在换流站2的交流侧发生三相交流故障后，由于交流电压持续下降，换流站2 传输的有功功率减小至零附近，直流系统出现功率缺额导致直流电压下降。此时，换流站1 独自承担系统直流电压稳定和功率平衡任务，致使其输送的有功功率随之增大。在3.15 s时，换流站2 交流侧的三相交流故障清除，交流电压逐渐恢复，送出的有功功率值提升，换流站1 与换流站2 共同作为功率平衡节点承担稳定直流电压的任务，最终系统恢复稳定。可见本文提出的控制策略具有较好的交流故障穿越能力。

在5.0 s 时刻换流站2 退出运行后，其传送的功率降至零，系统功率缺额导致直流电压下降。此时，换流站1 作为系统唯一功率平衡节点，承担系统直流电压稳定的功率平衡任务，其输送的有功功率随之增大。随着换流站1 传输功率的增加，K1*的值也在不断增大，最终输送的功率为1.53 MW；正负极直流电压稳定在11.9 kV，系统达到新的稳定运行点。

5 结论

VSC-MTDC 系统采用直流电压斜率控制时，由于未考虑各换流站的实际容量裕度，在系统出现剩余或缺额功率的情况时，可能会导致采用直流电压斜率控制策略的换流站满载而切换为定有功功率模式运行，失去了对直流系统潮流变化响应的能力。本文基于换流站容量裕度提出一种适用于VSC-MTDC 系统直流电压自适应斜率修正的控制策略，该策略无需换流站间通信，根据换流站的容量裕度自适应调节所承担不平衡功率量的大小，实现了直流系统功率的合理分配。PSCAD/EMTDC 软件平台的仿真分析表明，该控制策略可以满足不同运行状态下的要求，可以有效地维持系统功率的平衡和直流电压的稳定。