半无限Minimax离散化问题的一个大步长非单调SQP算法
杨永亮,王福胜
(太原师范学院 数学系,山西 晋中 030619)
0 引言
半无限Minmax问题是一类重要的优化问题,离散化方法是解决这类型问题的重要方法之一,基于离散化方法求解半无限Minmax问题可归结为求解一系列具有如下形式的半无限Minimax离散化问题:
(1)
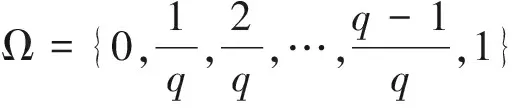
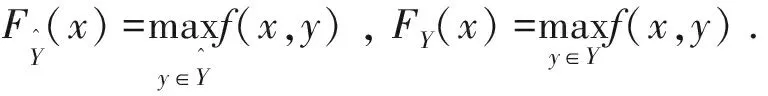
本文考虑固定离散水平q的问题(1),文献[1]中提出一种求解Minmax问题的非单调SQP算法该算法采用文献[2]提出的非单调技术,但在求解步长过程中由于每次迭代都需要更新参数,随着计算量的增加在求解过程中成为一种负担.Gu和Mo[3]克服这一缺陷提出了一种新的非单调搜索方式,其中的Ck是Ck-1和f(xk)的简单凸组合而数值实验表明该算法具有高效性、鲁棒性. Shi Z J和Shen J[4]提出一种新的大步长非精确线搜索技术,有利于算法的快速收敛.受文献[1-5]的启发,本文提出一种新的大步长非单调搜索准则结合模松弛SQP算法的思想,提出一个求解问题(1)的大步长非单调SQP算法.
1 算法描述
Ω-(x)={ω∈Ω|g(x,ω)≤0},Ω+(x)={ω∈Ω|g(x,ω)>0},
构造如下的QP子问题:
(2)

假设1.1 对于任意的y∈Y,ω∈Ω,函数f(·,y)和g(·,ω)均二阶连续可微.
假设1.2 对于任意的x∈Rn,Mangasarian-Fromovitz约束规格成立(简称MFCQ成立),即存在d∈Rn使得xg(x,ω)Td<0,对于所有的ω∈Ω成立.
受文献[2][4]的启发,本文所用到的大步长非单调线性搜索准则具体形式如下:
(3)
(4)

算法A
(H1)初始化.取适当大正整数q,将区间[0,1]离散成有限集ω,选取参数r0,r,rω,θ∈(0,1),σk,η∈(0,1)选取初始点x0∈Rn,对称正定矩阵H0∈Rn×n,并令k:=0.

(H3)求步长.由新的大步长非单调线搜索准则(3)获得步长αk.
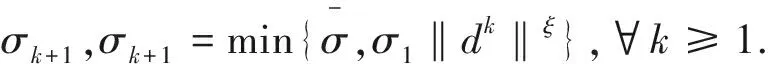
2 收敛性分析
本节将分析算法A的全局收敛性,设{xk}是算法产生的无穷点列,将证明{xk}的任一极限点x*都是问题(1)的一个稳定点,为此做如下假设:

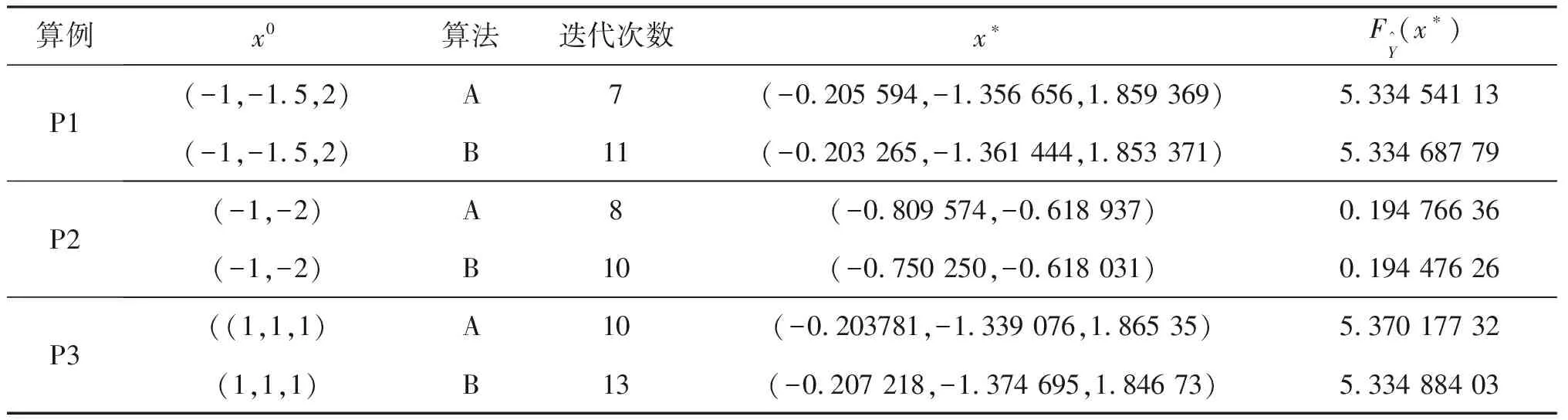
定理2.1假设2.1成立,αk由大步长非单调线搜索(3)产生,算法A生成一个无穷序列{xk},且0 (5) 证明:K1={k|αk=sk},K2={k|αk 因此, (6) (7) 如果k∈K2,则αk 对上式的左端等式由中值定理可知,存在一个θk∈[0,1],有 因此, (8) 由假设2.1和式(8)根据Cauchy-Schawarz不等式可得: αkL‖dk‖2/t≥‖xf(xk+θkαkdk/t)-xf(xk)‖.‖dk‖> 因此,αkL‖dk‖2/t>-(1-δ)xf(xk,y)Tdk,这表明 αk≥-[t(1-δ)/t]xf(xk,y)Tdk/‖dk‖2,k∈K2. (9) (10) 由式(3)和式(10)可得 -[δt(1-δ)(1-(1/2)γ)/L](xf(xk,y)Tdk/‖dk‖)2. 令ρ''=δt(1-δ)(1-(1/2)γ)/L,则有: (11) 令ρ0=min(ρ′,ρ″),由式(7)和(11)可得 (12) 推论2.1如果假设1.1,1.2,2.1成立且满足定理2.1中的条件,则有 (13) 进而序列{xk}的任一极限点是问题(1)的稳定点,即算法A是全局收敛的. 证明:类似于定理3.1证明,如果k∈K1,式(7)可知 (14) 如果k∈K2,由式(3)可得 由假设2.1可得 (15) 如果存在一个常数β0≥0,和一个无限子集K3⊆K2则有: -xf(xk,y)Tdk/‖dk‖≥β0,∀k∈K3, (16) 由式(15)和式(16)可得: (17) 由式(8)可得 xf(xk+θkαkdk/t,y)Tdk≥δxf(x,y)Tdk,k∈K3, (18) 其中θk∈[0,1]在定理2.1的证明中已经定义,由Cauchy-Schawarz不等式和式(18)得 ‖xf(xk+θkαkdk/t)-xf(xk)‖≥ ≥-(1-δ)xf(xk,y)Tdk/‖dk‖,k∈K3. (19) 由式(14)和式(19)且K1∪K2={1,2,3,…},可得式(14)成立.故算法A是全局收敛的. 本节将对算法A的有效性进行数值实验,在MATLAB2016a上编程序进行数值实验,结果见表1. 其中P1,P2,P3三个算例来源于文献[5],将算法与文献[6]中的算法B进行对比.参数如下: q=100,r0=5,r=1,rω=0.01,θ=0.1,γ=1,δ=0.38, 该算法的终止准则为|zk|≤10-4. 表1 数值结果 通过比较算法A和B,数值实验表明算法A的迭代次数较算法B有明显减少,近似最优值略有差距,在精度要求不太高的情况下大步长非单调技术对迭代次数的减少有一定的作用,可以认为该算法是有效的.
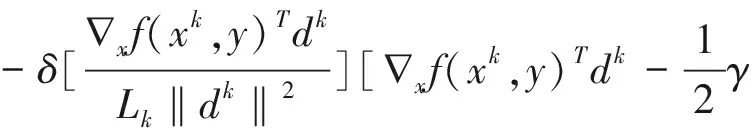





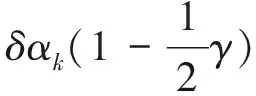


3 数值实验