基于地磁方位角的旋转弹丸姿态解算方法

安亮亮，王良明，赵丹丹

（1.南京理工大学 能源与动力工程学院，南京210094；2.辽沈工业集团有限公司，沈阳 110045）

地球磁场有着丰富的参数信息，利用地磁场来实现弹体的姿态测量具有全天候、能耗低、抗冲击能力强、无累积误差、可靠性高等优良特征[1]。近年来，随着集成电路技术的成熟以及反卫星武器的不断发展，地磁探测技术不断受到重视，广泛应用于航空航天、军事等领域[2-3]。

采用地磁传感器组合测量弹丸的飞行姿态参数，对于分析弹箭动力学、为导航制导系统提供支持等都有重要意义。常用的地磁传感器测姿方法大多依赖于坐标系转移矩阵，即载体坐标系与导航坐标系的相关转移。由于三姿态角的解算方程并不独立，需要假定某一姿态角为已知量，或者通过与内置弹载器件如陀螺仪、加速度计等进行数据融合来解算姿态角[4-6]，这些方法无疑大大增加了成本，而且由于载体小尺寸高转速的特点，也会存在传感器布局困难、姿态测量精度受限制等缺点。美国的研究人员最早提出了一种利用两个磁传感器输出信号所对应的零交叉点相位信息来测量旋转弹丸地磁方位角的方法[7]。南京理工大学在此基础上提出了一种基于非正交磁传感器组的极值比值法并做了相关研究[8-9]。文献[10]提出了一种比极值比值法精度更高的积分比方法，利用在高自旋环境中收集的所有地磁数据来计算弹丸姿态。文献[11]也在此基础上提出了一种相移比方法，简化了极值比-螺距角曲线的校准，并充分利用了测量数据。

在以上研究的基础上，本文通过分析稳定弹丸的外力矩情况，推导出了包含俯仰和偏航参数的弹丸绕心动力学方程组，然后基于磁方位角的物理原理，借助扩展卡尔曼滤波器（EKF）估计出了弹丸的俯仰角和偏航角。最后通过模拟仿真验证了该方法的有效性，并将该方法应用到实际工程项目中，也取得了预期的效果。

1 坐标系描述

1.1 地理坐标系O-NED

描述地磁场时，通常将地磁场磁感应强度M投影到北东地坐标系O - NED。如图1所示，以北半球为例，磁感应强度M所处垂面为磁子午面，X轴沿地理子午线向北为正，Y轴沿纬度线向东为正，Z轴垂直向下为正。

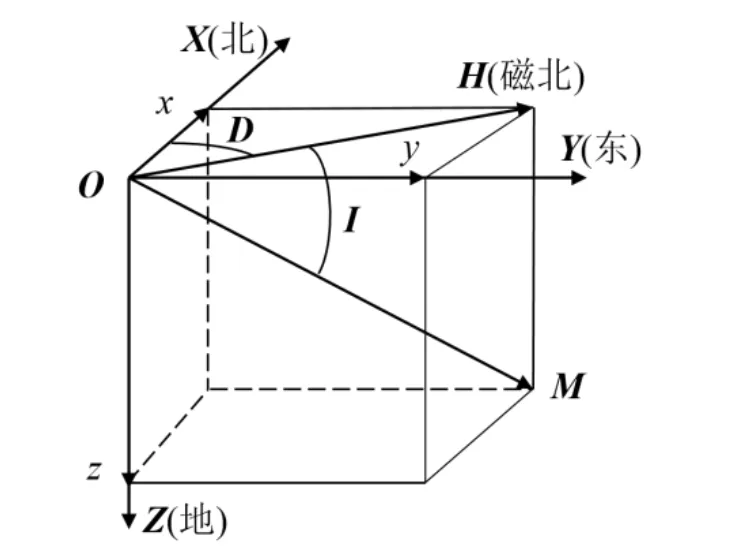
图1 地磁场参数Fig.1 Geomagnetic parameters

地磁场强度M在X、Y、Z轴上的投影x、y、z分别称为北向、东向以及垂直磁强度。M在水平面XOY面上的投影H 称为水平磁强度。磁子午面与地理子午面的夹角D 称为磁偏角，规定H 向东偏为正。M 与水平面的夹角I 称为磁倾角，在北半球，M指向地平线之下，磁倾角为正。

1.2 速度坐标系O-X2Y2Z2

速度坐标系 O - X2Y2Z2的 O X2轴沿质心速度矢量v 的方向，O Y2轴垂直于速度向上，O Z2轴按右手法则与 O X2Y2面垂直并向右为正。在速度坐标系中，速度矢量在铅直面的投影分量与水平面的夹角称为速度高低角θa，也称为弹道倾角；在水平面的投影分量与铅直面的夹角称为速度方向角ψ2，也称为弹道偏角。

1.3 弹轴坐标系O-ξηζ

Oξ轴为弹轴且向前为正，Oη轴垂直于Oξ轴指向上方，Oζ轴按右手法则垂直于Oξη平面指向右。Oξ轴在铅直面的投影与水平面的夹角称为俯仰角φa，在水平面的投影与铅直面的夹角称为偏航角φ2。

1.4 第二弹轴坐标系 O-ξη2ζ2

第二弹轴坐标系是由速度坐标系 O - X2Y2Z2旋转而来，Oξ轴仍为弹轴，先由速度坐标系 O - X2Y2Z2绕OZ2轴旋转δ1角到达 O - ξ′ η2Z2位置，再由 O - ξ′ η2Z2绕 O η2轴旋转δ2角到达 O - ξη2Z2位置，如图2所示。其中，δ1和δ2分别为高低攻角和方向攻角。弹轴坐标系O- ξηζ与第二弹轴坐标系 O - ξη2Z2的Oξ轴都是弹丸的纵轴，故坐标平面Oηζ与坐标平面 O η2ζ2只相差一个转角β。

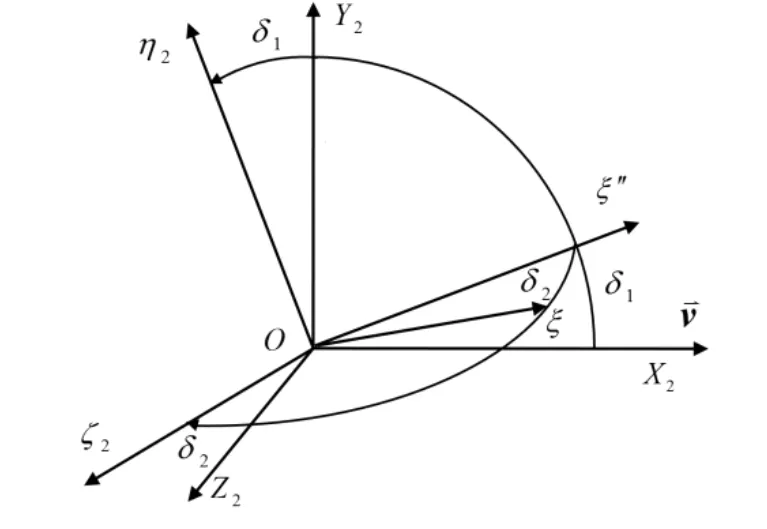
图2 第二弹轴坐标系与速度坐标系的关系Fig.2 Relationship between the second projectile axial coordinate system and the velocity coordinate system

2 基于零交叉点法的地磁方位角和滚转角测量

与弹轴夹角为λ的地磁传感器随弹体在地磁场中一起旋转时，沿传感器敏感轴的瞬时场强为[7]：

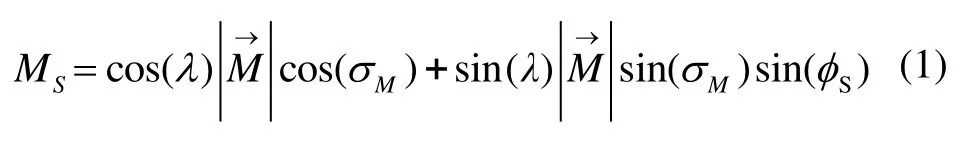
旋转弹丸在地磁场中飞行时，传感器的输出信号周期性地变化。当传感器轴与地磁场正交时，传感器的输出为零，即所谓的零交叉点。通过对两个地磁传感器的零交叉点进行判别和运算，就可以确定弹体飞行过程中相对于地磁场的方位角。

地磁传感器组合使用两个单轴地磁传感器，一个与旋转轴夹角为90°，另一个与旋转轴夹角为60°，如图3所示。

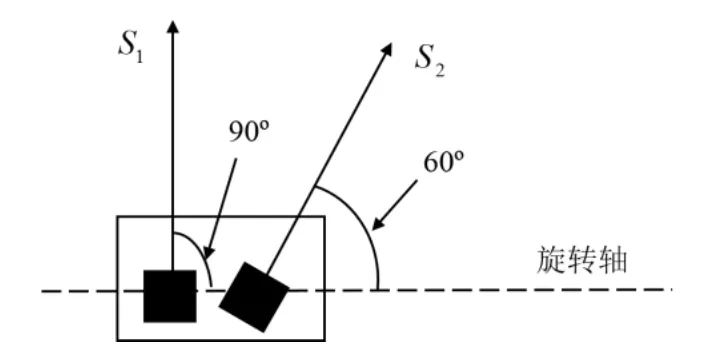
图3 地磁传感器组合安装示意图Fig.3 Installation diagram of geomagnetic sensor assembly

倾角分别为90°和60°的两个磁传感器S1、S2共面，当弹体滚转一周时，就会产生4个连续的零交叉点，对应于各自传感器的相位分别用和表示，则有比率：

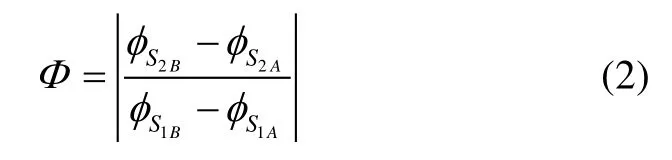
磁方位角σM与比率Φ之间存在着对应关系，其对应关系规律只与磁传感器S2的安装倾角有关，如图4所示，图中λ代表斜置传感器的倾斜角。

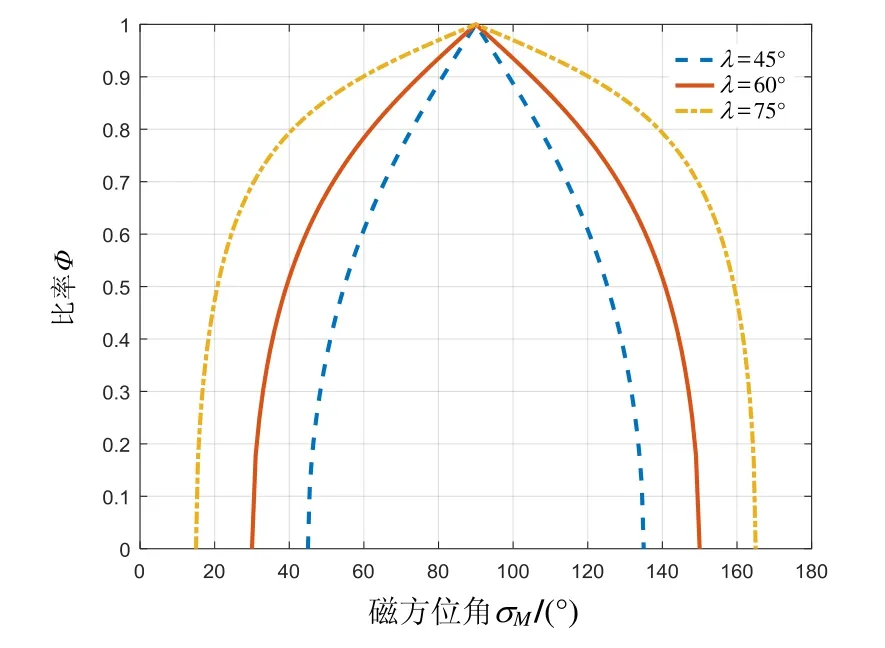
图4 比率Φ与磁方位角σMFig.4 Ratio (Φ) versus magnetic azimuth (σM)

比率Φ以σM= 90°为对称轴左右对称，因此除了对称轴之外，每个比率Φ都对应两个磁方位角σM，可以通过核查当 S2与磁场正交时沿 S1的磁场强度值的正负来确定取哪个值。

垂直轴传感器S1的安装倾角λ= 90°，则由式(1)可以得到沿传感器S1敏感轴的瞬时场强为；

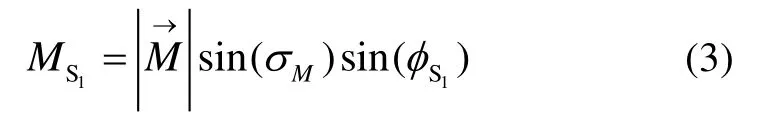
当磁传感器S1的敏感轴与地磁场正交时，传感器输出信号为零,即MS1=0。此时，sin(σM) = 0或者sin(φS1) = 0。而sin(σM) = 0意味着σM=0°或 180°，这种情况会在实验中规避。所以，当σM≠0°和 180°时，只存在 s in(φS1) = 0一种情况，则φS1= 0°或 180°，即相位组为(0°,180°)。

对于斜置轴传感器S2有λ= 60°，则沿传感器敏感轴的瞬时场强为：

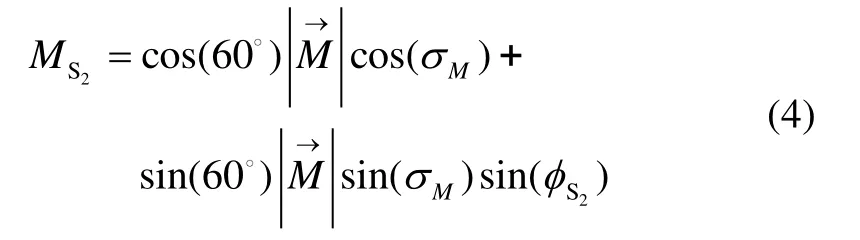
当磁传感器S2的敏感轴与地磁场正交时，传感器输出信号为零，即MS2=0。代入式(4)，计算得到：

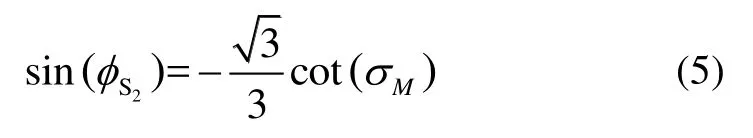
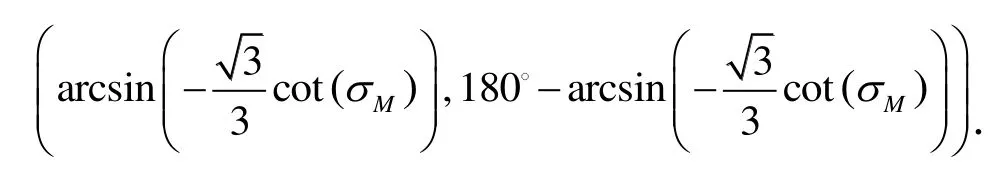
而在磁方位角σM已经确定的情况下，相位组可以计算出来。

零交叉点法相对于传统的坐标系转移方法，其优势在于将三姿态角信息(滚转角、俯仰角、偏航角)转换成两姿态角信息(滚转角、地磁方位角),将滚转角信息和地磁方位角信息分离为俯仰角和偏航角的单独解算提供了可能性。文献[7]详细讨论了零交叉点法解算得出的地磁方位角及滚转角的误差，其误差在10-3弧度的量级，满足二次数据处理的要求。

3 俯仰角和偏航角的解算方法

由于弹丸在空中的瞬时姿态可以由地磁方位角表示，而弹丸在空中的地磁参数是已知的（通过弹丸位置信息计算得到），所以弹丸的地磁方位角只包含俯仰角和偏航角两个未知信息。

弹丸的空中运动可分解为质心运动和绕质心运动。质心运动规律由质心运动定律确定，绕质心运动则由动量矩定理来描述，其中，绕质心运动决定了弹丸的姿态运动规律。假设无风，参考外弹道学中的弹丸绕质心动力方程组，结合实际问题组成新的方程组，如下：

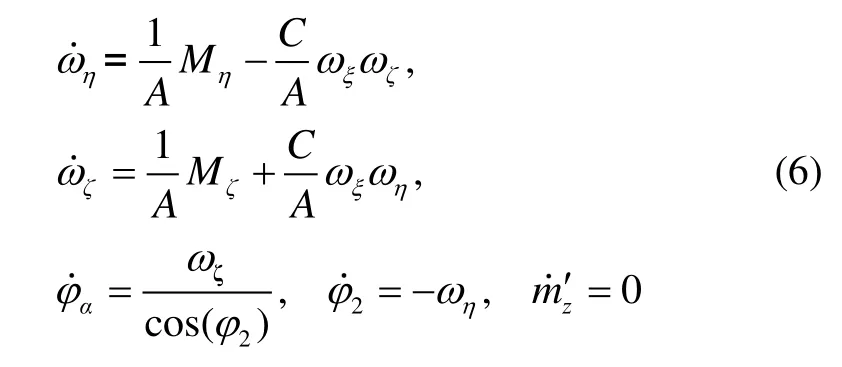
式中，Mη、Mζ为外力矩在弹轴系的分量，A、C为转动惯量系数，ωη、ωξ、ωζ为角速度分量，mz′为静力矩动导数，其中，

研究对象为高速旋转弹丸，只考虑静力矩。静力矩的向量形式如下：

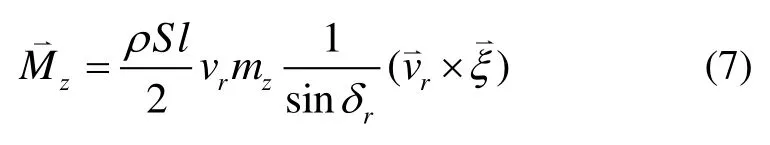
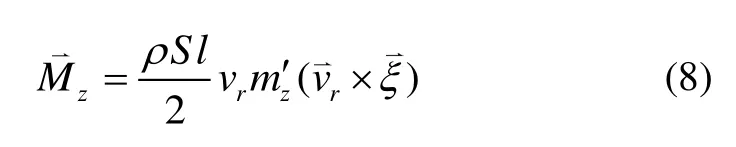
静力矩在弹轴坐标系上的投影分量形式为

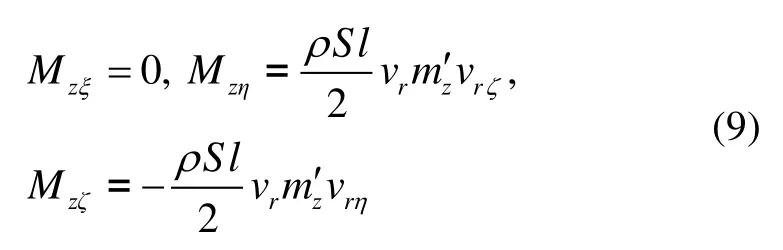
式中，vrζ和 vrη分别为相对速度 vr在弹轴坐标系上的分量，又记 vrζ2和vrη2分别为相对速度vr在第二弹轴坐标系上的分量，它们之间的关系为

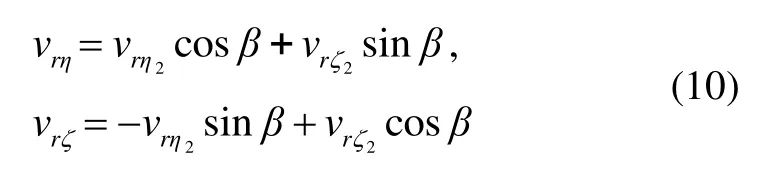
各坐标系内的方位角存在以下关系[9]：

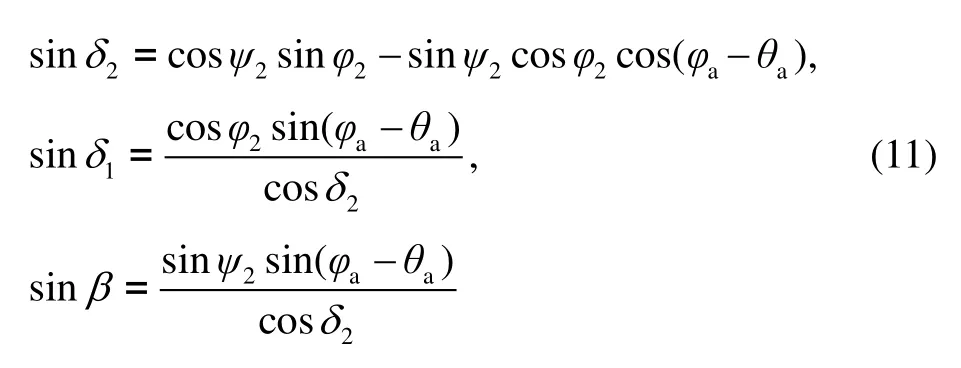
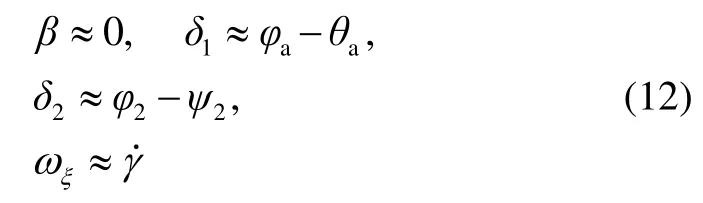
如图2所示，自速度坐标系向第二弹轴坐标系的转动关系可以得到则式(10)可以改写为：

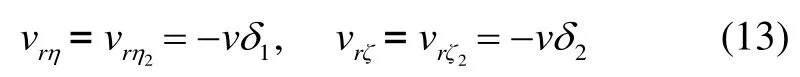
则静力矩分量可以写成：

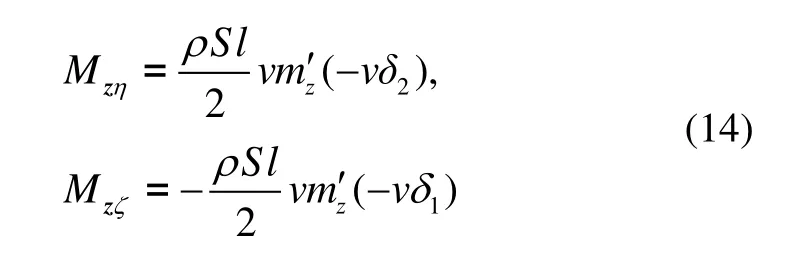
将式(12)代入式(14)，得到：

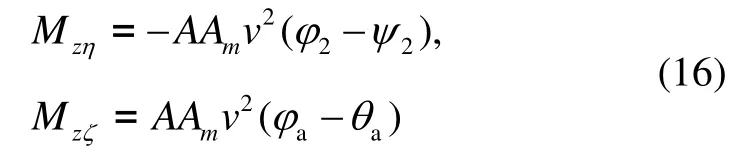
将式(16)代入方程组(6)，可以得到：

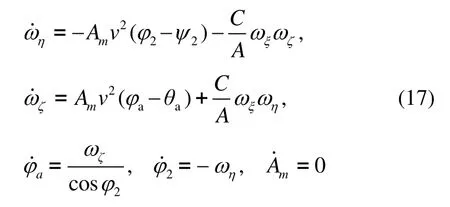
式中：弹丸的速度v 可以通过弹道雷达测量得到；弹道倾角θa和弹道偏角ψ2也可以通过速度分量计算出来；弹丸纵轴角速度ωξ由零交叉点法计算得到。

4 姿态解算方法的EKF滤波器构建

EKF的基本思路是对非线性函数的Taylor展开式进行一阶线性化截断，忽略其余高阶项，从而将非线性问题转化为线性问题。

4.1 状态方程

根据动力学方程组(17)取状态变量

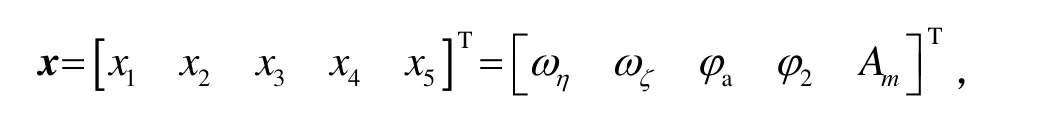
方程组(17)可以写成如下状态方程：

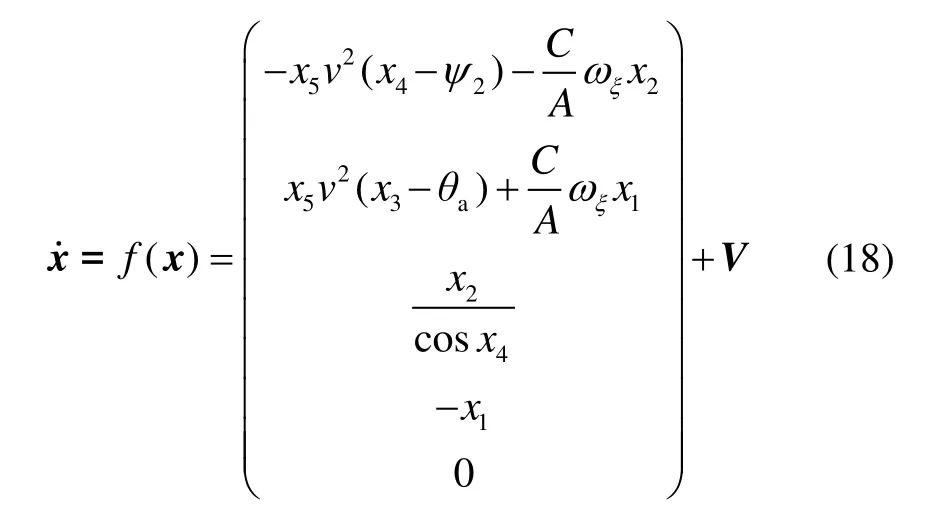
非线性方程(18)只是对弹丸运动的近似描述，存在一定误差，特引入一个高斯白噪声V，且 V ～N(0,R)。

4.2 量测方程

射向记为αN，不考虑子午收敛角的影响，将磁场矢量和弹轴矢量分别投影到地面坐标系中。

地磁单位矢量为

弹轴单位矢量为

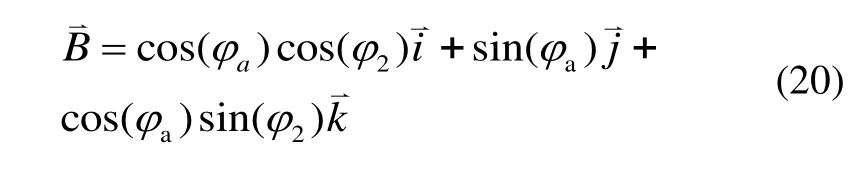
式中，由于研究对象为旋转弹丸，射程较近，所以全弹道过程中地磁变化很小，磁偏角D及磁倾角I可以视为定值。

地磁方位角σM是地磁矢量与弹轴矢量的夹角，根据向量夹角余弦公式可以得到：

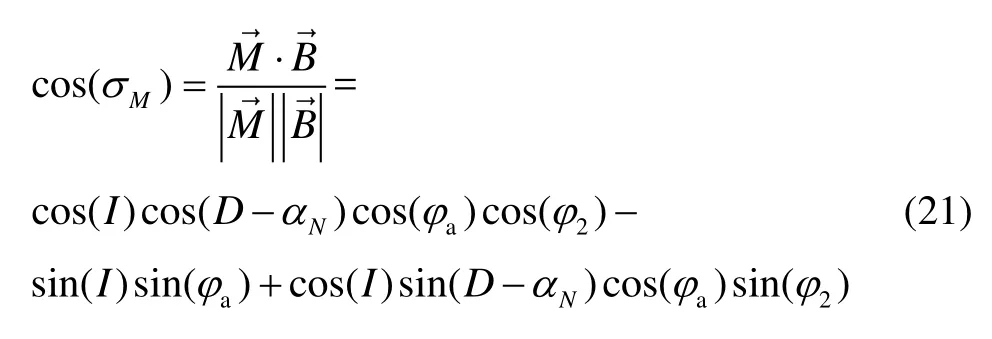
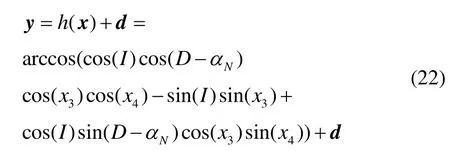
式中，d为量测噪声，

4.3 雅克比矩阵

对非线性函数的Taylor展开式进行一阶线性化截断，则取前两项为：

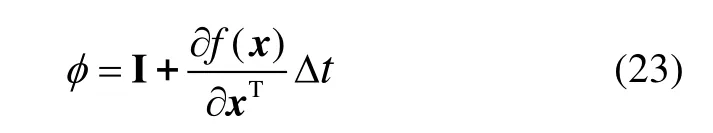
其中，Δt为采样间隔。

由状态方程(18)可得雅克比矩阵：

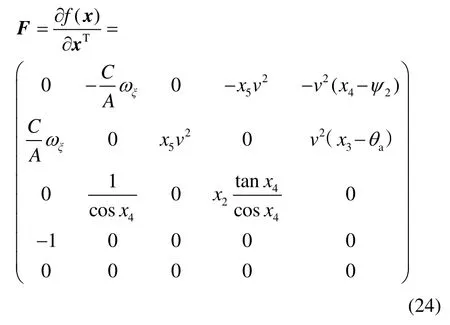
同理，通过量测方程(22)可得：

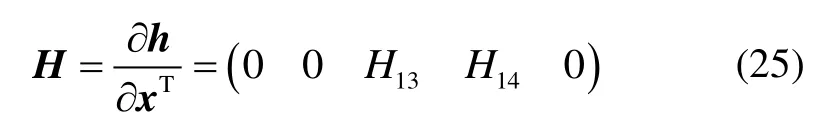
式中，

5 仿真验证及实验

5.1 仿 真

仿真以155 mm弹丸为模拟对象，假设弹丸以初速800 m/s发射,射角60°,射向100°。加入角速度高低分量2 rad/s和方向分量2 rad/s模拟初始扰动，仿真出全弹道数据；再通过弹丸的空中位置和相关坐标系的转移，模拟出全弹道的地磁参数；然后根据零交叉点法计算出弹丸的地磁方位角作为真值，滚转角真值则以弹道数据为准。

参照地磁传感器的性能参数设置误差，地磁方位角真值加入高斯白噪声V～N(0,(0.5°)2)作为量测值；滚转角真值加入高斯白噪声d～N(0,(1.5°)2)模拟带误差的滚转角计算值。图5为模拟的量测值与真值的误差,可以看出,地磁方位角的最大误差在±2°，滚转角的最大误差在±6°左右，远大于文献[7]提供的误差。

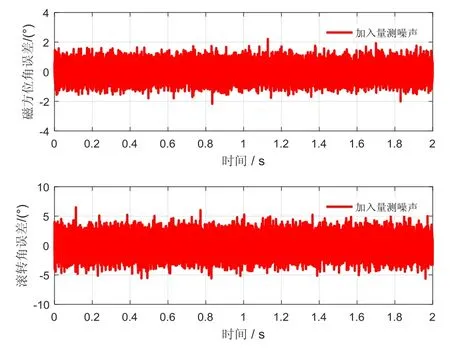
图5 加入的噪声Fig.5 Added noise

采用设计好的 EKF滤波器进行俯仰角和偏航角信息的估计,滤波结果与真值进行比较，如图6(a)所示，由图中可以看出，估计值与真值非常接近，整体规律一致，只在局部稍有不同，而且俯仰角和偏航角分别绕弹道倾角和弹道偏角周期性摆动且幅值不断衰减。图6(b)进一步展示了滤波的估计误差，由图中看出，俯仰角和偏航角的滤波误差整体趋势比较稳定，最大误差不超过0.2°。

从仿真过程及滤波结果来看，基于地磁方位角的姿态解算方法能够比较准确地估计出弹丸的俯仰角和偏航角，估计效果令人满意。即使量测值的误差较大，地磁方位角误差±2°，滚转角的模拟计算值误差为±6°，采用文中提出的解算方法仍然能够估计出精度较高的姿态角，最大误差不超过0.2°。

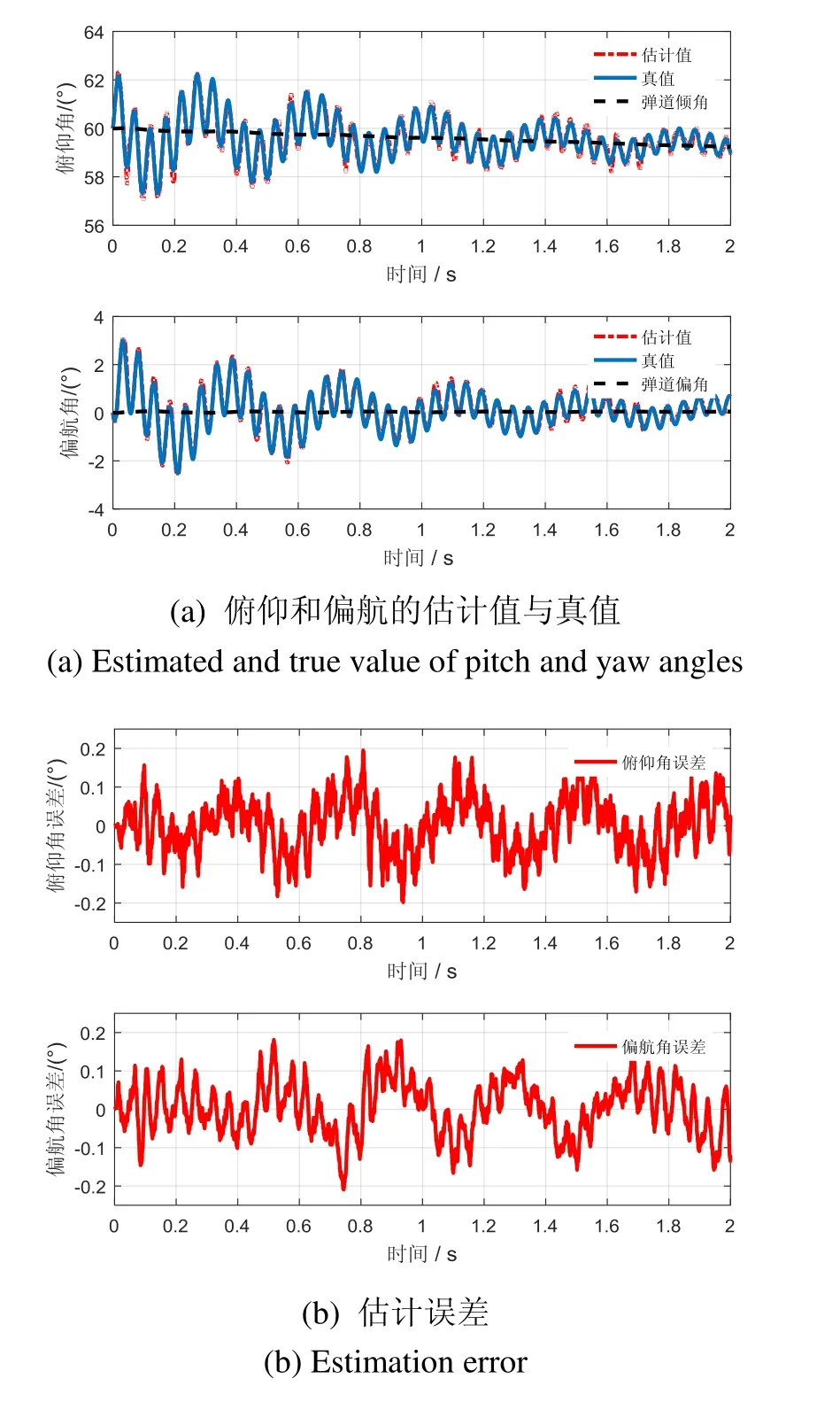
图6 解算结果与真值比较Fig.6 Calculation results versus true values

5.2 实弹实验及结果分析

对于射程达到几十公里的弹丸，以目前的技术水平无法直接观测其俯仰和偏航姿态，但是根据弹丸的运动规律和李雅普诺夫稳定性可以检验实验结果能否令人满意。在飞行过程中，旋转弹丸横向姿态（俯仰、偏航）的慢速运动项与速度方向是一致的，弹轴绕速度线呈周期性摆动且幅值不断衰减，这样才能保证弹丸的飞行稳定性。因此可以通过雷达测量得到的弹丸速度角信息(即弹道角信息)来侧面验证姿态解算方法的可行性。

实弹实验当天，天气晴朗，多云，无风，在炮位架设测速雷达以便测量弹丸的速度。将实验所使用的地磁传感器组件与弹体一起标定，以确保标定实验的准确性。准备完毕之后进行发射实验，射角为15.3°，射向为103.4°。

实验结束之后，选择其中一发弹丸的实验数据作为分析对象。为详细展示弹丸摆动规律，截取初始2 s的实验数据。雷达测量弹丸初速为 725.16 m/s。弹丸飞行过程中，磁传感器记录下各轴方向的地磁强度变化，然后根据零交叉点法解算出弹丸飞行过程中的地磁方位角及转速，解算结果如图7所示。地磁方位角初始值为117.6°，弹丸转速初始值为1486.39 rad/s。

然后采用设计好的EKF滤波器估计俯仰角和偏航角信息，并与测速雷达测量并计算得到的速度角信息对照，如图8所示。估计出的俯仰角和偏航角分别绕弹道倾角和弹道偏角呈周期性摆动而且幅值不断衰减，姿态变化规律稳定，符合李雅普诺夫稳定性定义。

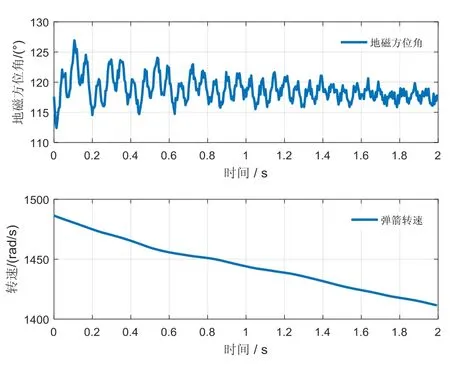
图7 地磁方位角及转速解算结果Fig.7 Calculation of magnetic azimuth and rolling speed

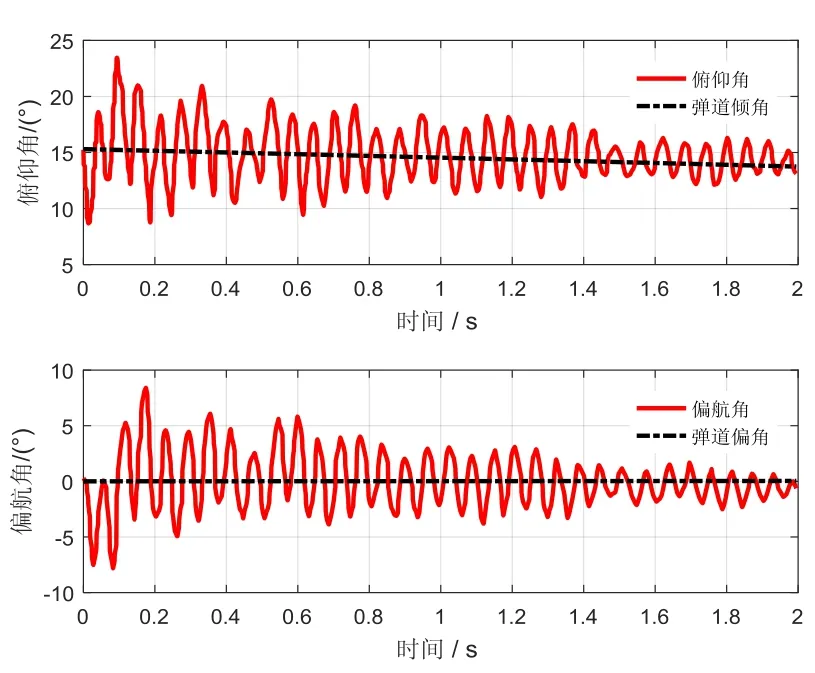
图8 俯仰角和偏航角的估计结果Fig.8 Estimation of pitch angle and yaw angle

再利用估计出的俯仰角、偏航角以及地磁参数计算出弹丸的地磁方位角，与零交叉点法解算的地磁方位角进行对比，如图9所示。从图中可以看出，由俯仰角和偏航角反向计算出的地磁方位角与零交叉点法吻合，这表明了俯仰角和偏航角的估计结果比较准确，达到预期效果。

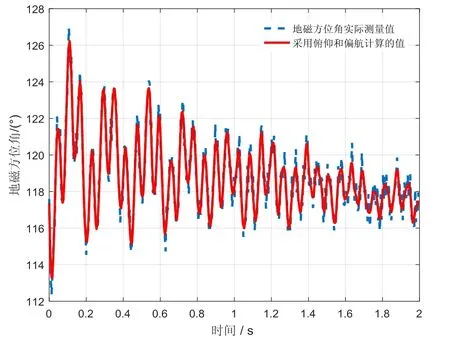
图9 地磁方位角测量值和计算值对照Fig.9 Contrast of magnetic azimuth between measured and calculated value

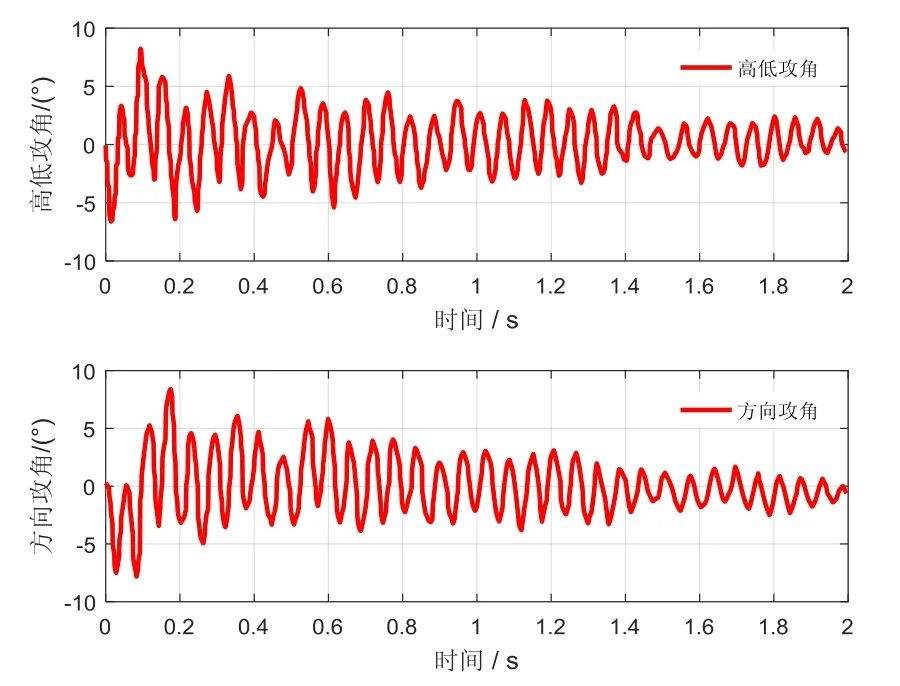
图10 攻角δ1和δ2Fig.10 Attack anglesδ1and δ2

对于正常飞行的弹丸，可以近似认为，估计得到的俯仰角与速度高低角θa的差值即为高低攻角δ1，偏航角与速度方位角ψ2的差值即为方向攻角δ2，如图10所示。这样对于测量弹丸的攻角信息也有帮助。

6 结 论

通过分析弹丸的旋转运动规律和受作用力矩情况，推导出了包含弹丸姿态角信息的动力学方程；再根据弹丸在地磁场的瞬时姿态建立起弹丸俯仰角、偏航角与地磁方位角的联系；然后借助EKF估计出俯仰角和偏航角信息。仿真表明，文中所提出的解算方法精度较高，最大误差不超过0.2°，证明了该方法的有效性。最后，将该方法应用到实际工程中，取得了预期效果，也证明了该方法的可行性。