基于SK等指标和SVM的滚动轴承性能退化评估研究

李 超，郭 瑜

(昆明理工大学 机电工程学院，云南 昆明 650500)

滚动轴承广泛应用于旋转机械中，其状态直接关系到机械设备能否正常有效运转，是机械故障诊断学科的重要研究对象之一。实际生产中，仅已知是否发生故障以及故障类型对于设备维修是远远不够的，只有了解故障演变的过程并掌握损伤严重程度，才能有效的组织安排制定维修计划，使生产效益最大化[1]。通常情况下，轴承的故障始于内圈或外圈表面下的材料疲劳裂纹，随着轴承的工作时长增加，裂纹会随之传播并最终达到表面，并使金属微粒脱离表面，即发生所谓的剥落和点蚀。在轴承状态监测中，当轴承因故障产生的金属碎屑达到一定量时，即被视为完全失效。振动信号分析是研究轴承性能退化评估的有效手段，基于振动的故障监测可以发现轴承性能退化过程中故障频率随着故障程度加深的演变规律[2]。

精密数控机床的电主轴滚动轴承的故障程度大小直接影响着机床的加工精度，及时监测不仅可以有效地掌握设备状态，还可以预防生产事故的发生。为了精确预测轴承故障的不同阶段，构造好的轴承性能退化指标在性能退化评估中非常重要。

传统的时域特征包括均方根(Root Mean Square，RMS)值、峭度、峰峰值和方差等。频域特征包括故障频率的1～6倍频幅值的平均数等原始特征，其随故障发展将呈现上升趋势，但这些特征对初期损伤不敏感，无法用来确定初期损伤时间[2-3]。

文献[3]提出对RMS进行标准化和滑移平均处理，得到相对均方根值(Relative Root Mean Square, RRMS)来作为一个敏感指标构建预测模型。但是RMS作为轴承性能退化的一种指标，其包含的故障信息对轴承的初期故障并不敏感。尽管文献[3]中对RMS进行了处理，但其包含的故障信息特性并不会发生变化，故其构造的模型不适合进行轴承初期故障的预测。文献[1]提出利用经验模态分解(Empirical Mode Decomposition，EMD)算法分解原始信号，结合能量与峭度条件找出蕴含故障本质的最优IMF分量，并在此基础计算最优分量包络的Lempel-Ziv，得到一种指示故障程度的Lempel-Ziv综合指标[1]。但是该方法采用人为加工的不同故障程度的轴承，进行数据采集以及后续的计算，与真实的轴承故障有一定差别，对实际工程应用缺乏说服力。文献[4]中使用变分模态分解(Variational Mode Decomposition, VMD)对轴承振动信号进行分解并提取特征判断故障虽然具有良好的鲁棒性。但该算法过于复杂，计算速度过慢影响轴承状态的实时监测。

谱峭度(Spectral Kurtosis，SK)用于包络提取[5]及齿轮、轴承等的早期故障程度监测[6]。鉴于SK对弱故障冲击的敏感性及故障初期随早期故障程度发展较好的上升趋势[7]，本文提出以SK作为轴承故障除去性能退化指标。在轴承退化程度阶段预测中，建立一个合理有效的模型是解决问题的关键。目前有一种基于神经网络的轴承剩余寿命预测模型被提出来进行轴承性能阶段监测[8]。但该模型需要大量的轴承试验来保证预测精度，因此在实际生产中难以实现。支持向量机(Support Vector Machine，SVM)是一种解决样本分类、模式识别和预测的机器学习算法。基于“one-against-one”方法的多分类SVM有助于解决多分类问题。

本文提出一种新的滚动轴承性能退化监测模型。通过采集振动信号、提取信号时域和频域信息、利用SK等多重指标进行性能退化评估，选取包含轴承各阶段特征的敏感信息作为输入，构造多分类支持向量机模型(SVM-OAO)来预测轴承性能退化的不同阶段。

1 多分类支持向量机

1.1 支持向量机原理

支持向量机(Support Vector Machine，SVM)由贝尔实验室的Vapnik[9]等人提出，用于解决二分类问题。现在有这样一组训练集{xi,yi},其中i=1,…,l，yi∈{-1,1}，xi∈RN。其中xi为原始样本，yi为样本所一一对应的标签及类别。对于线性可分的情况下，假设有一个分类面(也叫超平面Hyperplane)，该平面就是分类的决策边界，它可以把样本中的两类点分割开。最优超平面需满足

wT·xi+b=0

(1)

其中，w为超平面的法向量，b为偏置系数。

为了使最终得到的分类器鲁棒性更强，对于线性可分的问题，这些需要满足以下条件

兰德和荷兰政府经过5年的共同努力，建造了一个带有大型可移动门的风暴潮屏障，减少了荷兰环境、经济和安全方面的担忧。

wT·xi+b≥0,yi=1

(2)

wT·xi+b≤0,yi=-1

(3)

两边相乘可得

（124）中华光萼苔 Porella chinensis（Steph.）S.Hatt.刘胜祥等（1999）；赵文浪等（2002）；熊源新等（2006）；杨志平（2006）；

yi(wT·xi+b)≥1

(4)

SVM的核心在于找到离分割超平面最近的点并确保它们离超平面的距离尽可能的远，这些点即支持向量(Support Vector)。由式(3)和式(4)可得距离d

(5)

上述寻找最优平面问题可转化为如下的优化问题[9]

其他指标如峰峰值和偏度指标等也被用于指示轴承的衰退趋势。

（3）研究结果验证了融资约束的扩大振幅的作用，因此企业的融资约束程度需要控制在合理范围内，不能盲目地缓解企业融资约束。同时，实证结果显示代理成本的作用机制较为突出，企业应该完善内部治理机制，降低双重委托代理问题对海外直接投资经济后果的负向影响 （谢伟峰和陈省宏，2016）［15］。只有在公司治理和内部控制初见成效后解决融资约束问题，才是企业持续健康发展之根本。由于债权融资本质上也是借贷关系，对于降低企业杠杆率没有帮助，在企业杠杆率高企的当下，我国需要大力发展股权融资这一直接融资渠道，发挥股权融资在公司治理机制中的作用。

(6)

该问题为一个凸二次规划问题，且因式(6)中的不等式约束满足Karush-Kuhn-Tucker条件，可以通过拉格朗日对偶性来高效解决此问题。最终得到的分类超平面为

(7)

创业要实，常怀“担当之心”。敢于担当，面对矛盾敢于迎难而上，面对危机敢于挺身而出，面对失误敢于承担责任。善于担当，加强学习修养，注重实践锻炼，增强担当的本领。勤于担当，坚持“实”字当头、“干”字为先，在实干中解决问题，在实干中创造业绩。

RMS值是目前最常用的轴承性能退化指标之一，其对上述振动数据随时间的变化趋势如图2所示，其在第353小时才开始出现可察觉的上升趋势，对比图1(a)，在第307小时RMS只表现了微弱的起伏，可见RMS对于轴承的初期故障敏感性太差[16]。但在轴承故障的后期即353～361小时，有着稳定的上升趋势，说明RMS适合作为指示轴承性能退化阶段的后期指标。

某发电厂1000 MW机组汽轮机回热系统优化完成后，机组升负荷全过程锅炉给水温度平均值提高约9 ℃。90%THA负荷工况锅炉平均给水温度提高3.5 ℃；75%THA负荷工况为9.9 ℃；50%THA负荷工况为13.8 ℃。由于系统优化设计未充分考虑0号抽汽在低负荷工况存在较大的节流损失[19]，锅炉给水提升幅度小于优化方案预期。

但实际运用中难以找到一个合适的核函数使得训练样本在高维空间中线性可分，即使找到也难以确定这个线性可分的结果是否由过拟合导致。为解决该问题，可以允许支持向量机在一些样本的分类上出错。即一些样本点可以不满足式(4)。当然需要在最大化d的时候限制不满足式(4)的样本个数。因此引入惩罚系数C(C≥0)，并对每个样本点(xi,yi)引入一个松弛因子ζi，优化问题可转化为

(8)

齿轮或滚动轴承发生剥落或裂纹等故障时，在其发展的早期阶段会产生周期性的弱冲击，这些冲击又会激起对应的瞬态振动响应信号，故采集到的振动信号为脉冲性的周期性响应[13]。另一方面，采集到的振动信号经常被来源于设备中其他零部件所产生的较大背景噪声所干扰，如何在背景噪声下提取故障所对应的瞬态弱冲击特征是本领域研究的重要内容之一，也是谱峭度方法的优势。

(9)

本文提出将轴承的故障监测划分为4个阶段，属于小样本的多类模式识别问题。为解决此类问题，对支持向量机使用“one-against-one”策略。

式中，b*可以通过任一支持向量求解。

1.2 多分类方法

支持向量机的多分类方法，其中最适合本轴承性能退化评估方法的是“one-against-one”，即“一对一”的策略。该方法最早由Knerr等提出[10]，并由Krebel等[11]首次应用在支持向量机中。其原理为：对于多分类问题，训练集变化成{xi,yi},i=1,…,l，yi∈{1,…,k}，xi∈RN。每个yi对应一个xi，代表其属于的类。该方法的核心思想是在任意两类样本之间构建一个二分类分类器，总共需要k(k-1)/2个分类器。不失一般性，假设在第i个样本和第j(j=1,…,l)个样本之间构建了一个分类器，则可以将上述优化问题转换为

在k(k-1)/2个分类器构建好之后可以采取投票的方法来进行分类，即当样本xi之间通过上述分类器两两比较时，分类器指出该样本属于yi，则yi票数加1，否则yj票数加1。然后在预测过程中，任一样本xi的分类即是获得票数最多的那个[12]。基于“one-against-one”策略的支持向量机模型适用于分类数较少的样本训练和预测。

2 性能退化指标

2.1 谱峭度指标

最终分类超平面变为

本文首先采用辛辛那提大学提供的轴承全寿数据进行验证，失效形式为内圈故障，采样率为20 kHz。试验轴承型号为Rexnord ZA-2115双列圆柱滚子轴承，具体参数如表1所示。轴承的理论故障频率可由计算式(11)[14]计算得296.63 Hz。

表1 ZA-2115双列滚柱轴承的参数和试验条件

(11)

其中，n为滚动体的个数；fr为轴的转速；α为接触角；d为滚柱直径；D为节径。

如图1所示，为在0～10 kHz频率范围内1～361小时计算的所有SK值。从图1(a)中可看出，307～320小时SK值出现了比之前高的值，此时轴承的出现初期的剥落故障。随着轴承的继续旋转，可以推断336～343小时该剥落故障逐渐发展，在344小时可能发生较大剥落，冲击强度增大，SK发生突变。这一系列变化在4 kHz以上时尤为明显，如图1(b)所示。说明了SK可以排除低频强背景噪声的干扰，并有效指示出轴承初期故障的发生。

为满足现阶段人类社会生存与发展的重大需求，科技创新发展优先领域的选取既要与时俱进，考虑经济的可持续增长，又要结合实际，应对当下科技创新挑战。对比2009年和2011年美国创新战略，可以发现医疗保健、清洁能源、教育技术和空间探索一直是美国全力推动的优先发展领域。随着全球信息技术的快速发展，2015年美国创新战略进一步将智慧城市和计算机前沿技术纳入优先发展领域[5]，见图2。下面详细介绍2015年美国创新战略的优先发展领域及取得的成效。

2.2 谱峭度与其他常用指标的对比

在构建轴承性能退化程度监测模型中，选取可以反映轴承性能退化过程的指标非常重要。常用指标包括RMS、峭度、峰峰值、偏度等[2,15]。下面依次列这些常用指标对上述相同数据的轴承性能退化程度的指示情况以便与SK指标进行对比。

我国是世界上大豆消费数量最多的国家，且大量依靠进口。2016年我国大豆进口量达 8 391万t，价值339.8亿美元，占全世界大豆进口总值的67%[2]。相比之下，2014年国内大豆产量仅为 1 215万t，占当年大豆进口量(7 140万t)的比例不到1/5，且近年来国内大豆产量呈缓慢下降的趋势[3]。进口大豆依存度高并未影响我国对转基因大豆严格的安全性要求，截至2017年年底，尚未有一种转基因大豆通过农业部转基因生物安全评价被商业化种植。

这样的一体化生产似乎可以奏效。价位在700到4500瑞士法郎之间，这家厂商显著增加了机心供应，从两年前的6000枚到如今的22000枚。Vaucher Manufacture生产五大类“VMF”机心。“我们的目标是从现在起5年之后达到35000枚。目前，60%的产品销往帕玛强尼和爱马仕。我们的外部客户包括Harry Winston、Richard Mille和昆仑。”

对于线性不可分的情况，支持向量机可以引入满足Mercer条件的核函数K(xi,xj)=Φ(xi)·Φ(xj)，将原样本中的各个点映射到高维空间，在高维空间中建立一个最优的超平面以解决问题。

图3(a)所示为峭度指标，由于在正常情况下，轴承的全寿命试验无法模拟实际工况(排除了轴承信号在采集过程中所受到的背景噪声和低频干扰)，故在辛辛那提轴承全寿命内圈数据的基础上添加了低频周期冲击仿真信号用作对比。图3(b)为添加了仿真信号后提取的峭度趋势。图3(a)中峭度值随时间的变化趋势在前期很平稳，并可以和SK一样确定初期故障发生的时间第306小时。但是在图3(b)可见峭度受到低频周期冲击信号的影响，在第191小时的峭度值比306小时还要高，无法正确的指示出轴承初期故障的发生时间。其原因是峭度的统计学特性使得其对非高斯性过于敏感，而非高斯性即强脉冲信号往往会把微弱的非平稳信号所掩盖[17]。轴承的故障信号属于弱非平稳信号。在实际的信号采集中，信号中会混入大量的复杂低频噪声，导致峭度既不能提供稳定的趋势也不能确定具体的故障时间。

历史学习有着一定的时间限制，由于事件发生的时间相对较远，学生对当时的社会状况缺少一定的认识，不能对历史进行充分理解。但是科学技术的发展为教育教学提供了多媒体教学设备，教师可以通过多媒体信息技术为学生提供相关的历史视频与音频资料。例如在学习中国抗战胜利，中华人民共和国成立的课程内容时，教师可以通过视频资料的播放，让学生身临其境地感受祖国的伟大胜利。

两湖地区属楚文化范畴，范围主要包括湖南、湖北等地区。楚文化崇尚浪漫，生活在两湖地区的人们富有浪漫情怀，同时湿润的气候适宜竹材的生长，竹文化在这里繁荣昌盛。浓郁的楚文化对两湖地区的影响，造就了两湖地区鲜明的竹编风格，其中以湖南的益阳竹编、湘西竹编为代表。

如图4和图5所示，分别是时域中的峰峰值指标、最大值、最小值和偏度(第3节中心距)。其中峰峰值、最大值对初期故障也有一定的敏感性，但是信号中的噪声较多；最小值最初期故障没有敏感性但能反映出整体的退化趋势；偏度可以勉强反映出整体的退化趋势，但是指标中的信息过于嘈杂，故不适合作为轴承性能退化的指标。

图3(c)为加入仿真信号之后的SK，其整体趋势和初期故障的指示与图1(a)趋势基本一致。可见与谱峭度相比，峭度值易受周期冲击性噪声干扰。

SK作为轴承早期性能退化评价指标具有以下优点：(1)SK对初期故障敏感，可以准确指示故障发生的初始时间，并可以随着故障程度增长；(2)与时域指标相比，SK不仅看到整体退化趋在时域上的变化，还可以看到故障发生的频域位置，帮助排除了低频噪声的干扰；(3)SK可以不受故障发生位置的限制，具有通用性。

3 轴承性能退化评估方法

3.1 敏感特征选取

由以上分析可知，谱峭度指标能较好地反映早期阶段轴承性能退化情况。如图1(a)所示是图1(b)在4 575 Hz频率切片图中307小时的SK值明显升高，较清晰的指示出了初期故障的发生；另一方面，初期故障发生后，经过一段时间的摩擦，剥落区边缘会被逐渐钝化，此时谱峭度值会发生暂时性的低落。因此，轴承性能退化评价仅采用谱峭度指标并不适合，还需要对中后期更加敏感的RMS值指标以及峰峰值等其他指标来辅助进行4个阶段训练样本的划分。

3.2 轴承性能退化阶段预测模型

性能退化预测的流程图如图6所示。首先需要轴承全寿命的时域振动信号；其次提取谱峭度指标、RMS等敏感性指标和表征整体趋势的指标；然后利用上述指标分割出轴承退化状态的四个阶段(正常、初期、中期和后期)；再将指示4个阶段的指标作为训练样本输入模型，训练基于多分类支持向量机SVM-OAO的轴承性能退化阶段预测模型；最后在测试过程中，处理实时采集到的时域信号，提取出谱峭度、RMS和其他敏感指标作为测试样本，输入到基于多分类支持向量机的轴承性能退化阶段预测模型中，模型即可预测此时的轴承退化处于哪个状态。

3.3 评估模型验证

试验使用了内圈故障轴承全寿命数据，提取前述3种敏感性指标，即谱峭度、RMS和峰峰值。内圈故障的3种指标变化趋势如图1(a)、图2和图4所示。图1(a)中，在307小时SK突然增高，图4峰峰值，在307同时增高，而RMS此时没有变化，可判定为初期故障开始；图1(a)中344小时，SK达到最大值，344小时之后迅速下降，此时峰峰值略微增高，RMS无明显变化，轴承在此时进入中期故障阶段；图2所示353小时后，RMS突然增高，此时轴承进入后期故障阶段。

然后根据上述分析总结出轴承性能退化的4个阶段划分的方法为：正常状态下，SK值、RMS和峰峰值处于平稳状态；初期故障发生时，SK值突然增高、峰峰值有明显上升趋势并达到最大值且RMS没有变化；中期故障发生时SK会降低但较比正常状态时高，峰峰值趋于平稳或略微下降，RMS不发生变化；后期故障发生时，RMS和峰峰值突然增高。

为了验证模型的有效性，将3种指标划分成表征4个阶段的样本，把样本放入模型中进行训练， 得到预测模型。选取了内圈故障轴承全寿命数据中正常到后期阶段的数据(内圈测试数据Ai、Bi、Ci、Di，)进行测试，结果如表2所示。

表2 内圈故障轴承全寿命故障阶段模型测试

表2中显示的是模型对测试样本分类的概率(模型对样本的敏感度)。在表2中，Ai样本的预测结果是正常状态，预测正确，其中模型对于处于正常状态的样本敏感度很高；Bi、Ci预测结果也正确；Di虽然预测结果正确，但是中后期的敏感度较接近，原因是训练样本中SK所占比例很大，训练样本的信息融合还可改进。从验证的结果可见该评估方法可以进行轴承性能退化4个阶段的正确划分。

4 基于全寿命的试验验证

为进一步验证所提方法的有效性，研究中在ABLT-1A轴承疲劳寿命试验机上进行了轴承全寿命实验，实验台架如图7所示。试验轴承为6205单列深沟球轴承，加载径向载荷5.8 kN，电机转速为3 000 rpm，采用32#机械油润滑。采样频率为51.2 kHz，每隔5 min保存一次数据，每组数据51 200个点。轴承自然失效类型为外圈剥落故障，具体参数如表3所示。

参数数值轴承外径/mm52轴承内直径/mm25接触角/(°)0滚动体直径/mm7.938滚动体数9内圈滚道直径/mm30.562外圈滚道直径/mm46.438

轴承疲劳试验同时测试了4个轴承，选取一组外圈故障轴承数据来进行轴承性能退化阶段预测模型的试验验证。

来去学校我得拿一个书篮，内中有十多本破书，分量相当沉重。逃学时还把书篮挂到手肘上，这就未免太蠢了。凡这么办的可以说是不聪明的孩子。许多拿篮子逃学的小孩子，人家一见就认得出，上年纪一点的人见到时就会说：“逃学的，赶快跑回家挨打去，不要在这里玩。”若无书篮可不必受这种教训。因此我就想出了一个方法，把书篮寄存到一个土地庙里去。我把书篮放到那地方去，次数是不能记忆了的，照我想来，搁的最多的必定是我。

首先提取了谱峭度、RMS和峰峰值指标作为训练样本。全寿命试验数据的指标如图8～图10所示，图11为谱峭度图在25.6 kHz的频率切片。

然后将轴承的正常期、初期故障期、中期故障期以及后期故障期的指标分别构成4个状态的训练样本，输入评估模型。最后随机抽取未用作训练样本的数据进行测试，结果如表4所示。

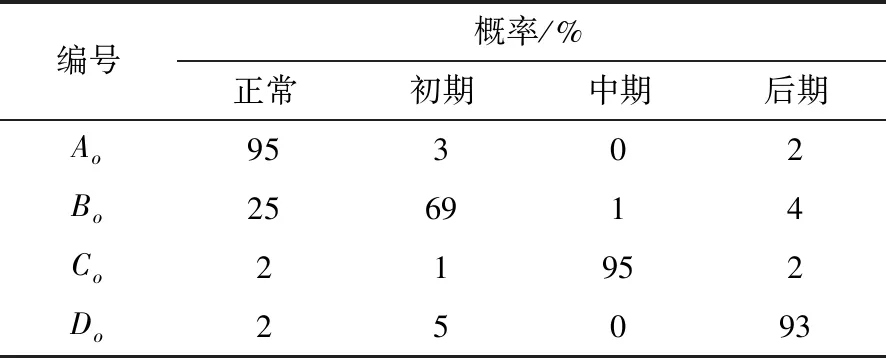
表4 6205型轴承全寿命故障阶段模型测试Table 4. Full-life fault stage model test of 6205 bearing

如表4所示为本文所设计模型的准确率，预测结果正确且准确率高。4组测试样本虽然得到的分类概率虽然较好，但是并非完全正确，故还可进一步完善模型。

5 结束语

本文提出的基于多重指标选择和支持向量机的滚动轴承性能退化阶段预测模型能够有效的预测轴承故障阶段。弥补了轴承性能退化评估中对于分阶段预测的空白。文中验证了谱峭度作为初期故障指标的合理性和有效性，以及对于轴承故障阶段预测模型具有很强的可操作性以及工程实用价值。下一步工作会针对训练样本的信息融合和模型进行优化，提高模型对后期故障的预测的准确性。