谐振式MEMS压力传感器的设计与分析

许高斌，胡海霖，徐枝蕃，陈 兴，马渊明

(合肥工业大学电子科学与应用物理学院，安徽省MEMS工程技术研究中心，安徽合肥 230009)

0 引言

谐振式压力传感器是高精度压力传感器中的典型代表，在现代航空航天领域具有非常重要的作用，它通过检测谐振器的固有频率间接测量压力，不需模数转换，信号采集和处理方便，适用于远距离传输[1-3]。它比常用的扩散硅压阻压力传感器以及其他模拟式压力传感器具有更高的精度和更好的长期稳定性，一直是研究和开发的热点，在国际上受到广泛的重视。

硅微谐振压力传感器常见的4种驱动方式中，电磁激励方式必须外加恒定磁场[4-5]，光激励方式光学系统复杂[6]，组装精度要求很高，因此，均难以实现微型化，电热激励方式[7-8]易受外界环境温度变化影响。而静电激励方式是一种非接触的驱动方式，不会影响谐振器的振动品质因数，响应快、功耗低、灵敏度高。在静电激励硅微谐振压力传感器方面，英国Druck公司[9]和法国Thales公司已取得一系列成果并成功商品化。但其谐振器振动方向垂直于压力敏感膜片，因此精度受同振质量影响。虽然Druck 公司利用侧向振动谐振器对其结构进行了改进[10]，谐振器与压力敏感膜片工作模态互相垂直，避免了同振质量的影响，但当压力敏感膜片受压变形时谐振器的高度会发生变化，因此，仍存在不稳定驱动与检测的问题。

本文设计一种静电激励/压阻检测的硅微谐振式压力传感器，工作振型为2个质量块平行于压力敏感膜片的面内动平衡反向振动，基于绝缘体上硅(SOI)的加工工艺，利用硅-硅键合技术进行传感器的真空封装，并通过TSV通孔互连技术实现传感器与电路的三维混合集成。

1 工作原理与理论模型

1.1 工作原理

硅微谐振压力传感器芯体的总体结构方案如图1所示。谐振器主要包括质量块、谐振梁、拾振电阻3个部分。当有外界压力作用时，压力敏感薄膜发生形变，该形变通过硅岛结构传递并放大到谐振器固定端，从而改变了谐振梁的弹性刚度，谐振器固有频率改变；与此同时质量块随着敏感薄膜的变形也发生位移，压敏电阻的阻值发生变化，此时输出电压频率和固有频率不一致，当闭环电路反馈在梳齿上的激励电流频率几乎为谐振器谐振频率时，谐振器发生谐振，当振动达到平衡时，此时输出电压频率为谐振器固有频率。在一定的压力范围内，谐振器的固有频率与待测压力有稳定的正比例对应关系，通过检测该固有频率变化就可以实现压力检测。

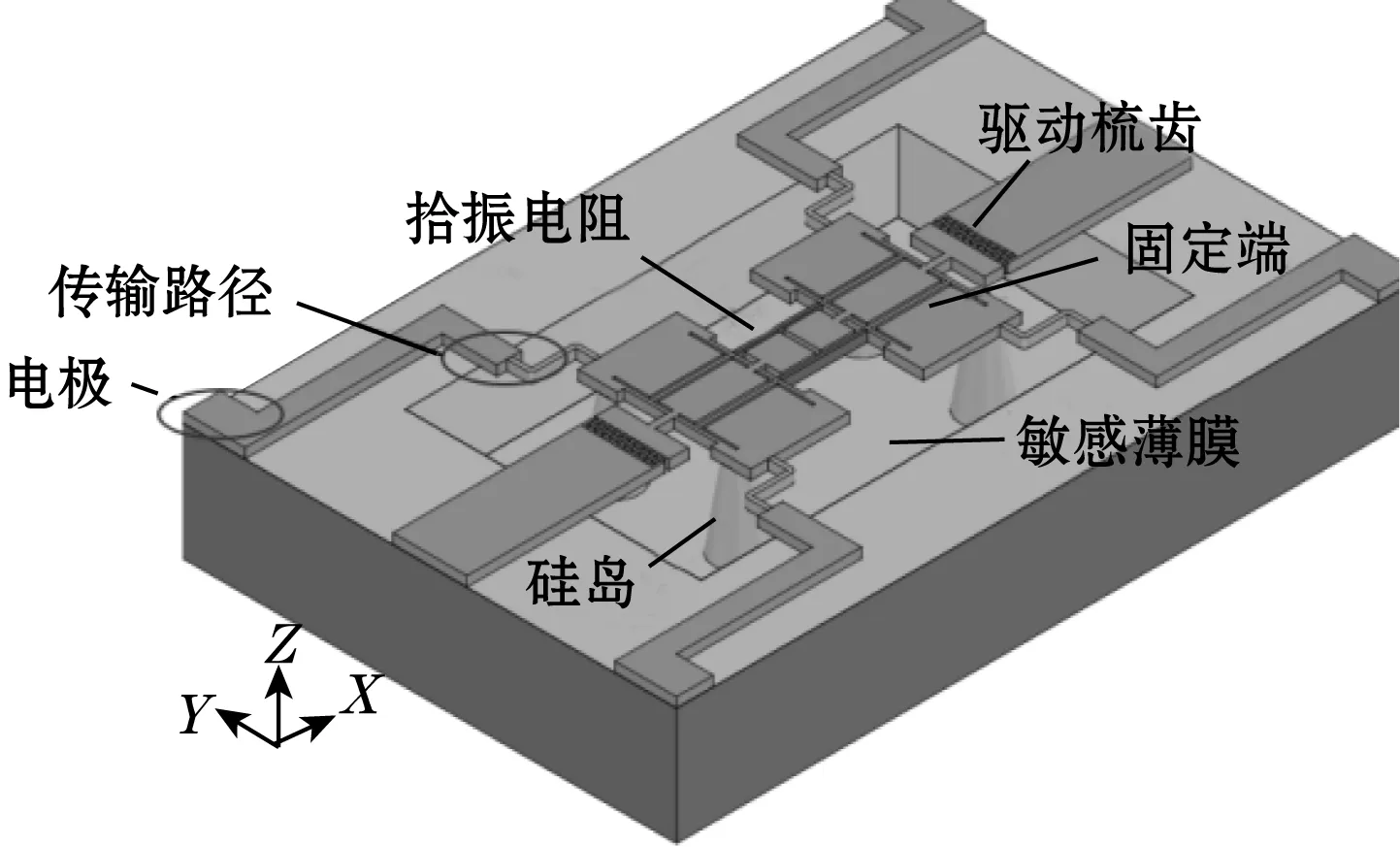
图1 硅微机械谐振式压力传感器三维结构图

在静电驱动下，谐振器发生谐振如图2所示，工作模式为2个质量块于XOY平面内动平衡反向振动，2个拾振电阻与等效体硅电阻组成惠斯登电桥，并通过电桥得到由于压力变化导致的压阻材料阻值变化，从而达到检测谐振器谐振频率的目的。另外，拾振电阻还起着将2个质量块耦合在一起的作用，保证即使在驱动力和谐振器结构存在微小不对称的情况下传感器在整个工作过程只有1个稳定的振动模式和谐振频率，因此其工作更加稳定，Q值更高。

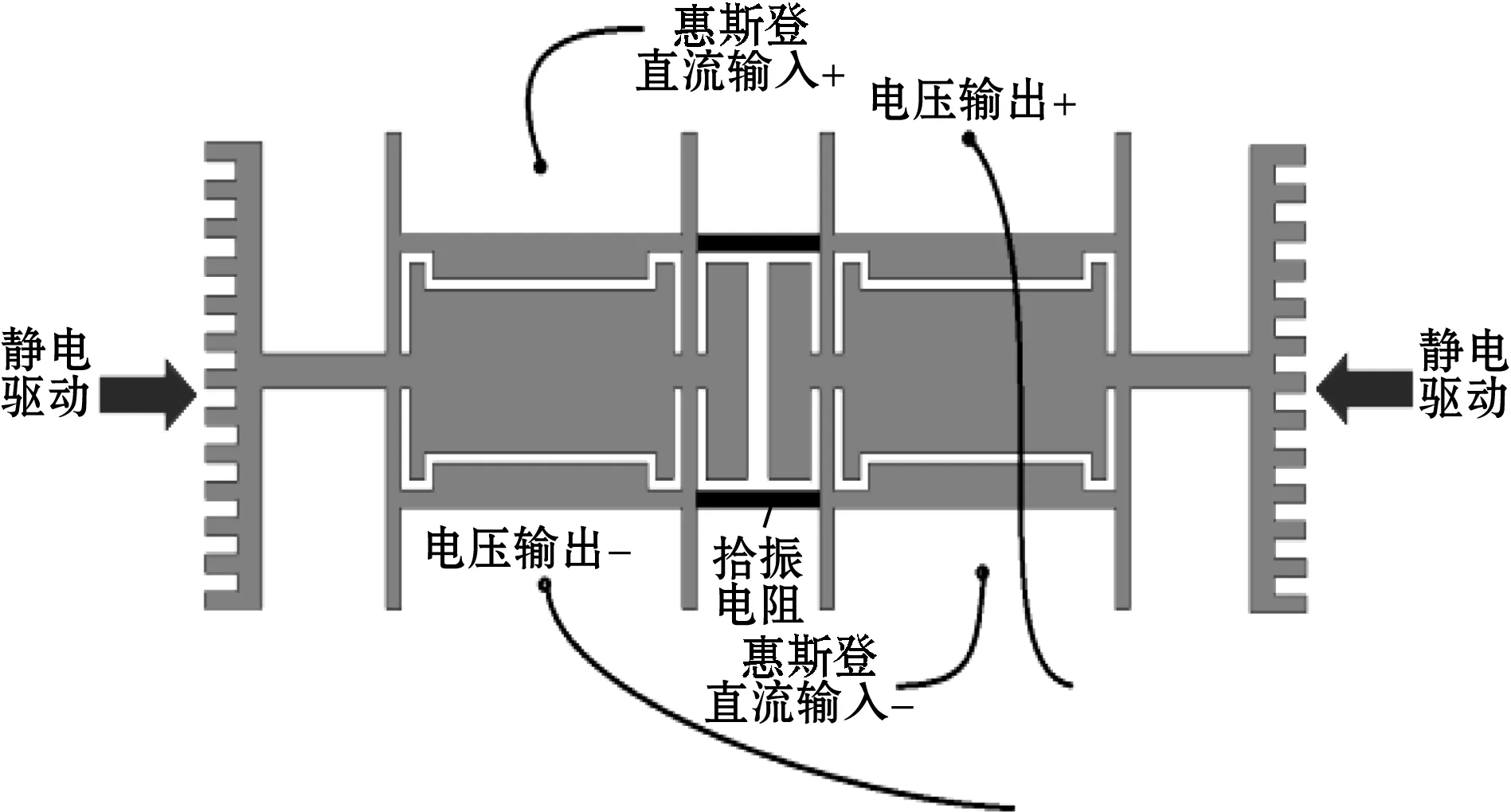
图2 谐振器的电学连接图

该压力传感器等效力学模型如图3所示，其谐振器与压力敏感膜片的工作模态互相垂直，而2个正交二阶系统的振动能量相互独立且不会互相传递，虽然当压力敏感膜片受压变形后，谐振器与压力敏感膜片的工作模态将无法保持绝对垂直，谐振器振动过程中的交变振动力会产生垂直于压力敏感膜片的分力，从而引起谐振器与压力敏感膜片在垂向的能量耦合，但通过增大压力敏感膜片的垂向弹性系数，同时增加谐振器和压力敏感膜片的工作模态频率间隔可以抑制该分力的影响，从而保证传感器精度不受同振质量的影响。

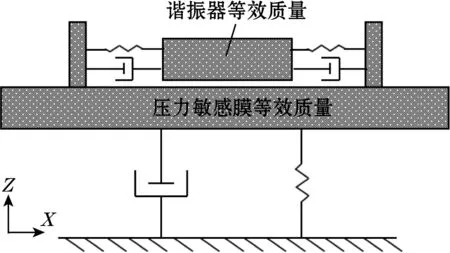
图3 硅微谐振式压力传感器等效力学模型

1.2 谐振梁弹性系数分析

如图4所示，将谐振梁看成2个直梁以及中间横梁组成。由理论力学可知，在本结构中，中间横梁可看作刚度棒，因此单个直梁的刚度k1可表示为梁a和梁c的刚度组合，并令靠近质量块一端为梁a，令ka和kc为梁a和梁c的刚度，其定义为[11-12]

(1)

式中：I=hb3/12；h为梁厚；b为梁宽；E为材料杨氏模量[13]；la和lc分别为谐振梁a和谐振梁c的长度。

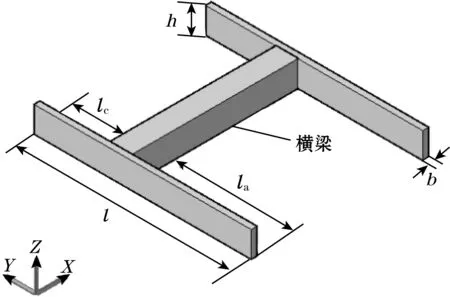
图4 谐振梁结构示意图

故可得单边梁刚度为

(2)

梁受轴向应力情况下单边梁刚度为

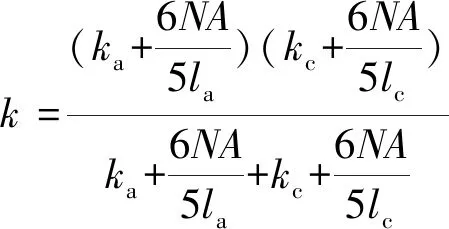
(3)

式中：A为谐振梁横截面积,A=hb；N为谐振器的轴向应力，N=E·Δl/l,Δl为梁的轴向位移，l为包括横梁、梁a、梁c的单边梁长度。

谐振器固有频率可表示为

(4)

式中：meff为谐振器的等效质量，meff=mp+mf+mc+0.375mb，mp为质量块质量，mf为梳齿质量，mc为横梁质量，mb为直梁质量；keff为谐振器刚度系数。

在轴向应力N下，谐振器频率为

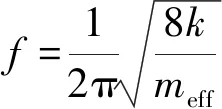
(5)

1.3 敏感膜与谐振器之间应力传递分析

梁受固定端应力后的轴向位移Δl可由以下公式求得[14]：

(6)

式中：y1为硅岛与敏感膜边之间的距离；ΔH为硅岛高度；θ为受力情况下的敏感膜变形角。

为更好地说明Δl与ΔH之间的关系，对Δl求关于ΔH的导数，其结果为sinθ(0°≤θ≤90°)，因此当ΔH越高，Δl越大，由于敏感薄膜的变形小，θ为锐角，可近似表示为

θ≈arctan[ω(0,B-y1)/y1]

(7)

式中ω(x,y)为敏感膜任意点挠度。

假设敏感膜片上压力载荷均匀分布，利用薄膜变形理论在小变形情况下，矩形膜片在外界压力作用下的解析公式为

(8)

式中：ω为膜片任意点挠度；ω0为膜片中心点最大挠度；A为敏感膜X向半边长；B为敏感膜Y向半边长。

(9)

(10)

式中：p为薄膜所受压强；E为材料杨氏模量；υ为泊松比；H为敏感膜厚度。

(11)

式中：μx为任意点处x轴方向位移；z为该点距膜片垂向中心对称面的距离。

(12)

式中μy为任意点处y轴方向的位移。

(13)

式中：σx、σy、τxy分别为X向、Y向、切向应力。

由于膜片结构对称，取Y轴进行研究，令x=0，z=H/2。可得矩形膜片表面Y轴处的应力为

(14)

2 器件设计

2.1 谐振梁设计

谐振器在实际工作工程中主要承受2个力：敏感膜片受压变形传递到梁固定端的轴向力；谐振器双端梳齿产生的静电驱动力。因而会在梁的弹性系数中引入非线性成分，因此在结构设计上要尽量减小该非线性成分[15]。敏感方向(X向)外力F与梁导向固定端位移x对应关系：

(15)

式中：l为梁长；A为梁横截面积；E为材料弹性模量；I为转动惯量，I=hb3/12，h为梁厚，b为梁宽；三次项与一次项比为18/25b2。

图5为梁宽与非线性比例关系曲线。因此要抑制该非线性对谐振器固有频率的影响，要尽量增大谐振梁宽度，谐振梁宽度越大，工艺误差对传感器性能影响越小，但谐振器的应力灵敏度越低。综合考虑，最终取谐振梁梁宽为15 μm。

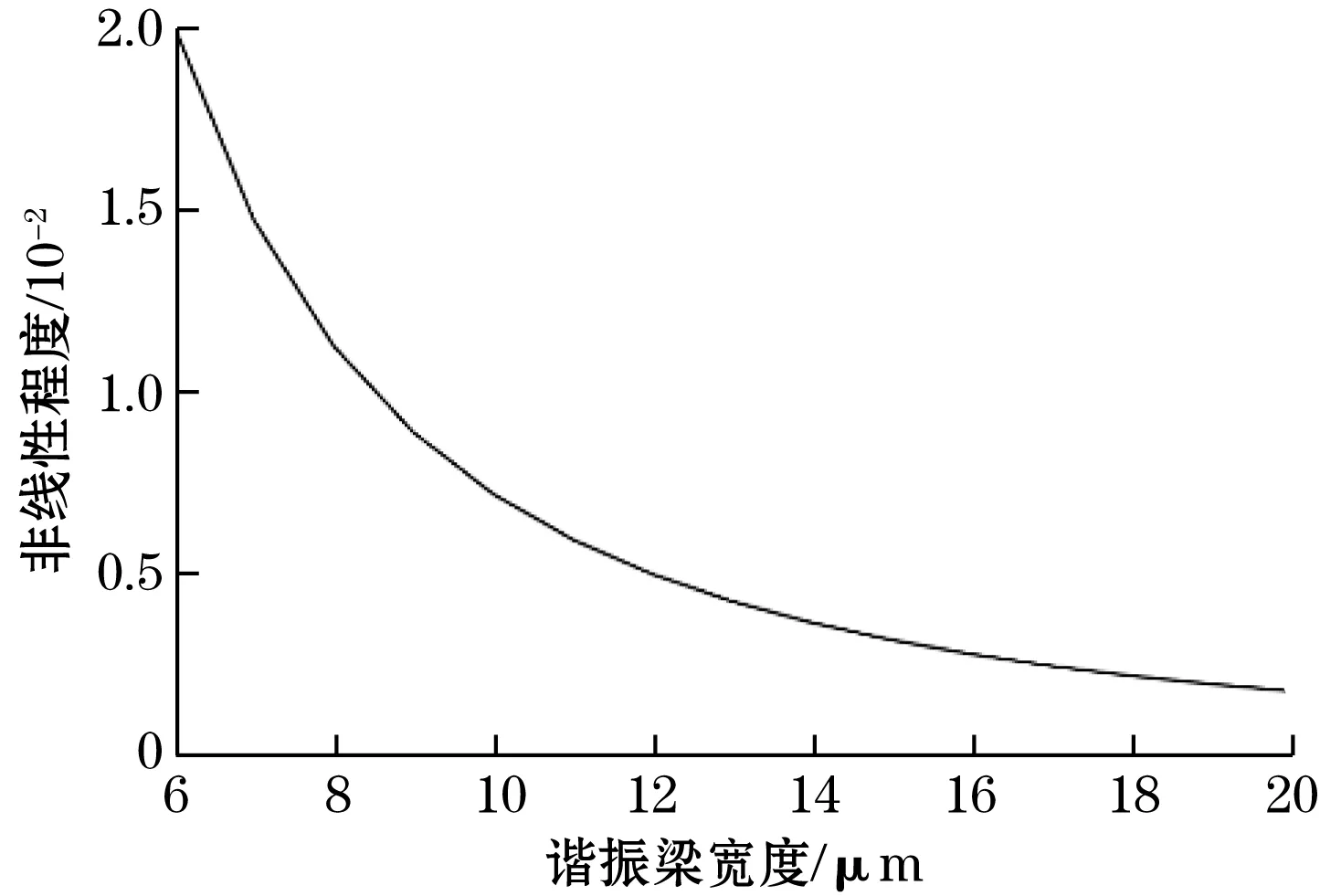
图5 非线性与梁宽的关系曲线

梁横截面对X轴和Z轴方向的惯性矩为：Ix=bh3/12，Iz=hb3/12。由此可知h/b的比值越大，越有利于抑制谐振器的Z方向振动，保证Z向振动模态与工作模态之间具有足够大的频率间隔，取梁厚h为70 μm即谐振器层厚度为70 μm。

另外对于本结构来说，谐振梁单边梁中梁a与梁c的比重不仅影响着谐振器的固有频率，还可以通过调整二者比重来调节谐振器的一阶模态与工作模态间隔。最终取梁a长342 μm，梁c长192 μm。

2.2 谐振器固定端设计

当压力敏感膜片受压变形时，会导致谐振器的高度发生变化，存在着不稳定激励与检测以及传感器精度受同振质量影响等问题。设计如图6所示固定端结构方案。当压力敏感膜片受压变形时，支撑柱会向外侧倾斜，因此，桁架末端高度相对于支撑柱顶部会下降，从而抑制谐振器的高度抬升。同时为了进一步抑制谐振器的高度变化，要尽量减小压力敏感膜片的受压变形量，而为了保证传感器精度则需要进一步提高谐振器的应力灵敏度。

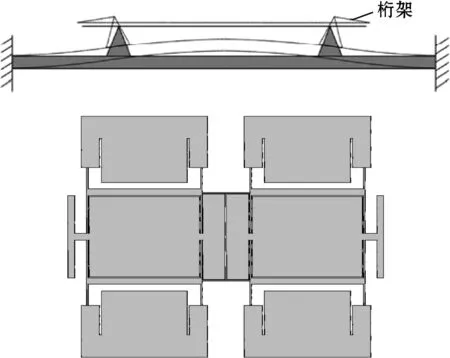
图6 谐振器固定端结构视图

2.3 压力敏感膜片与硅岛设计

由1.3节分析可知，考虑矩形敏感膜的对称性，取Y轴进行研究，根据式(8)和式(12)，令x=0，z=H/2。其矩形敏感膜表面位移特性如图7所示，横轴代表Y轴上各点，纵轴分别代表对应位置Y轴上各点位移，令R=ω0H/A。

图7 敏感膜表面Y轴上各点位移

取单晶硅材料参数，E=169 GPa，υ=0.23，计算得到敏感膜表面Y轴应力分布如图8所示。横轴代表Y轴上各点，纵轴代表对应位置X向和Y向应力令Q=2EHω0/(1-υ2)。

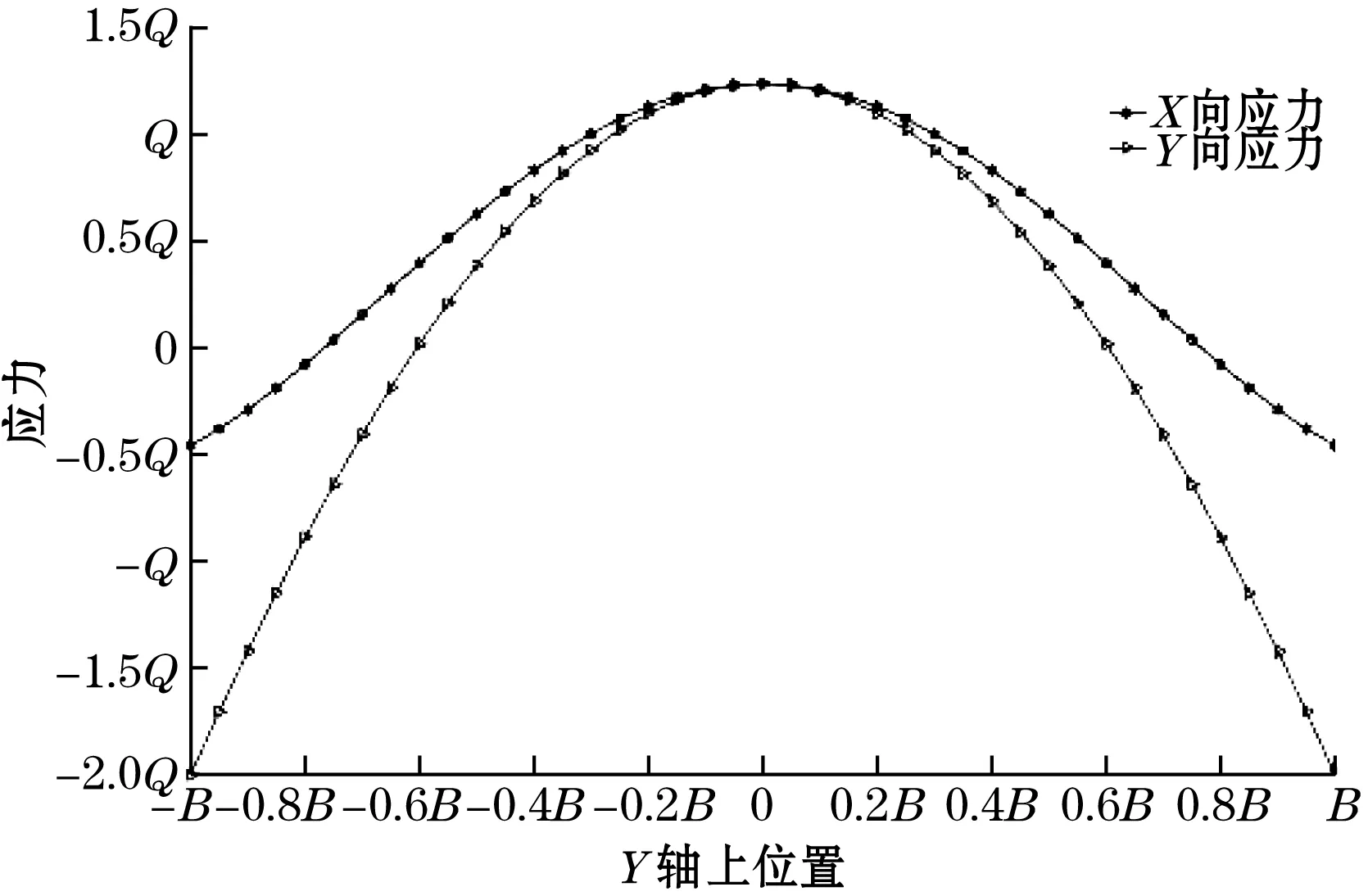
图8 正方形敏感膜表面Y轴上各点应力

由上述分析可知，当外界待测压力作用在压力敏感膜片上时，最大挠度位于敏感膜片中心，最大Y向位移位于±0.6B处。且该处的Y向应力为0，属于最小应力区域。因此，在设计硅岛时要遵循以下原则：

(1)硅岛要布置在敏感膜片偏转角度最大的位置，以放大膜片在谐振器敏感方向上的位移量，提高传感器的灵敏度；

(2)硅岛要布置在低应力区域，以避免应力集中；

(3)硅岛的设计要利于工艺实现。

因此将硅岛布置于±0.6B附近可以最大限度地提高传感器的灵敏度。同时抑制谐振器因压力敏感膜片受压变形引起的高度变化以及满足强度要求。故根据谐振器和固定端的设计参数可得敏感膜片尺寸为3 462 μm×2 308 μm，长宽比为1.5。

3 仿真分析

为进一步验证理论计算。在有限元仿真软件ANSYS中对设计的谐振器结构进行仿真，表1汇总了传感器的主要参数。

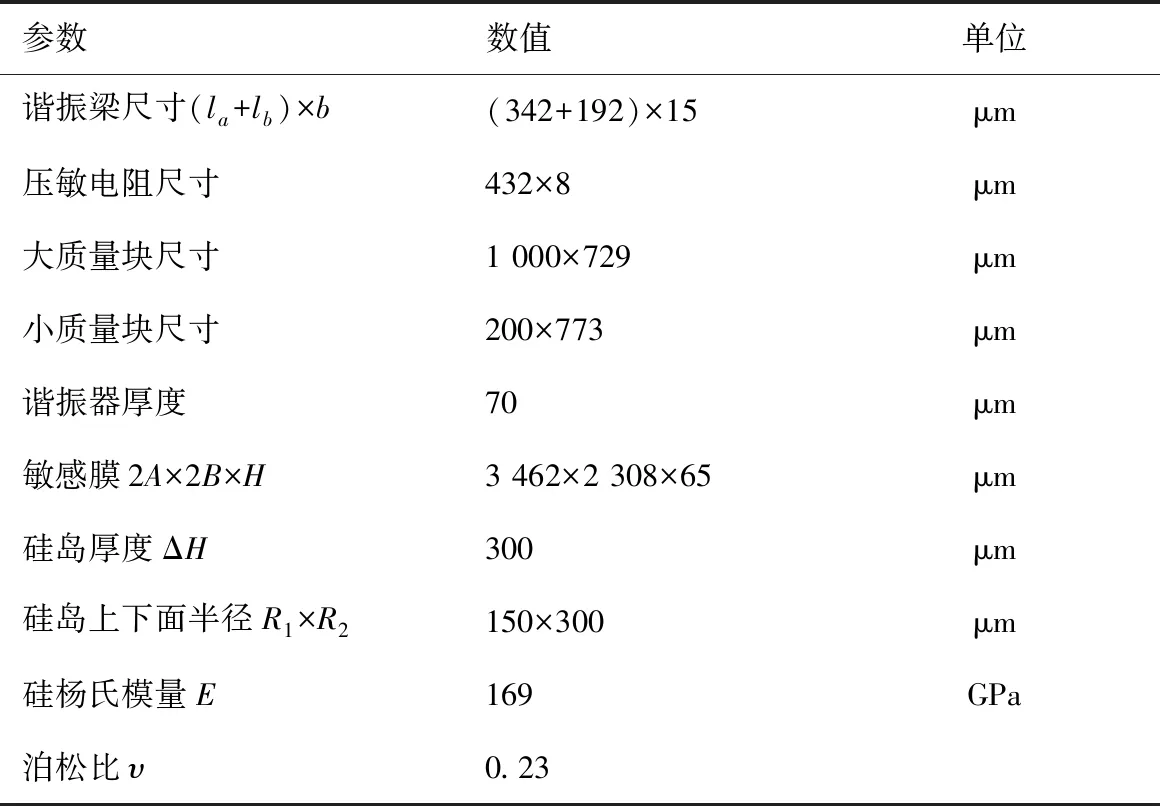
表1 传感器几何尺寸和材料参数

本文采用2阶振动模态为传感器的工作模态，如图9所示，为无轴向应力情况下的前六阶振动模态，工作模态频率为24.013 kHz，一阶模态与二阶模态的频率间隔为2.245 kHz。

图10表示在0～100 MPa拉应力下工作模态谐振频率的变化曲线，综合1.2节所述，曲线与理论相符，谐振器具有明显的单向应力敏感特性。该特性有利于提高传感器的稳定性，增强传感器的抗干扰能力。

压力敏感膜厚度决定着其受压变形的能力，从而影响着传感器的压力灵敏度，如表2所示，利用有限元分析在120 kPa与180 kPa 2个压力载荷下，分析敏感膜厚度对传感器性能的影响。限制在满量程压力下谐振器梳齿的Z向位移小于0.4 μm，最终选择压力敏感膜厚度为65 μm，其满量程压力下频率变化量为9.059%，最大应力为97.912 MPa，梳齿最大高度变化0.380 4 μm，满足设计指标要求。

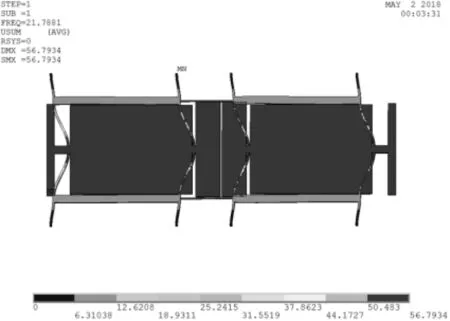
(a)1阶模态(21.768 kHz)

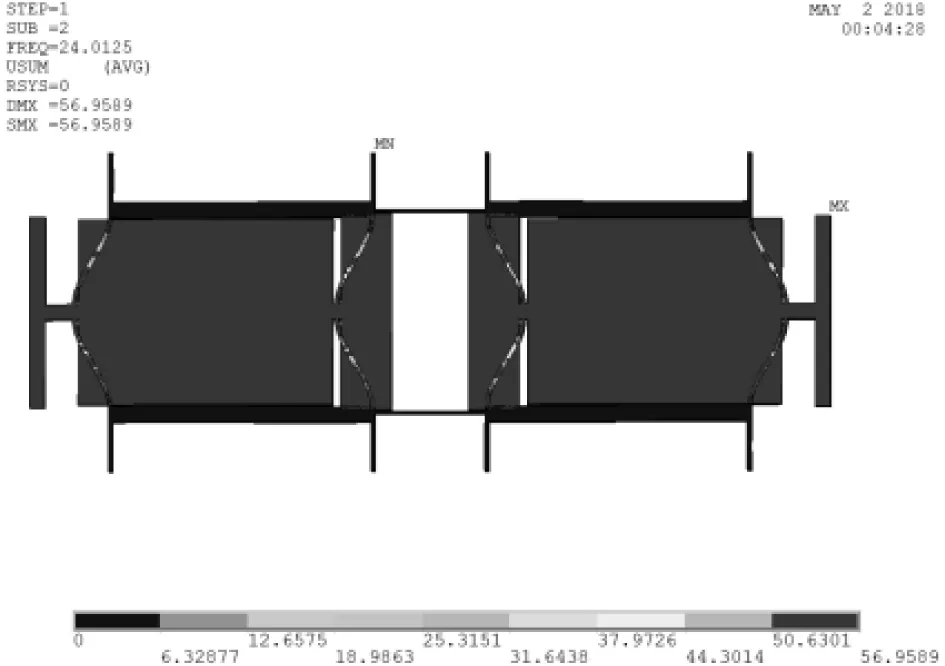
(b)2阶模态(24.013 kHz)

(c)3阶模态(47.896 kHz)

(d)4阶模态(49.998 kHz)

(e)5阶模态(76.277 kHz)

(f)6阶模态(78.738 kHz)

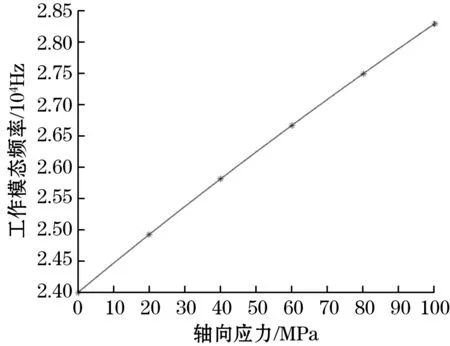
图10 轴向应力与谐振器工作模态频率对应关系

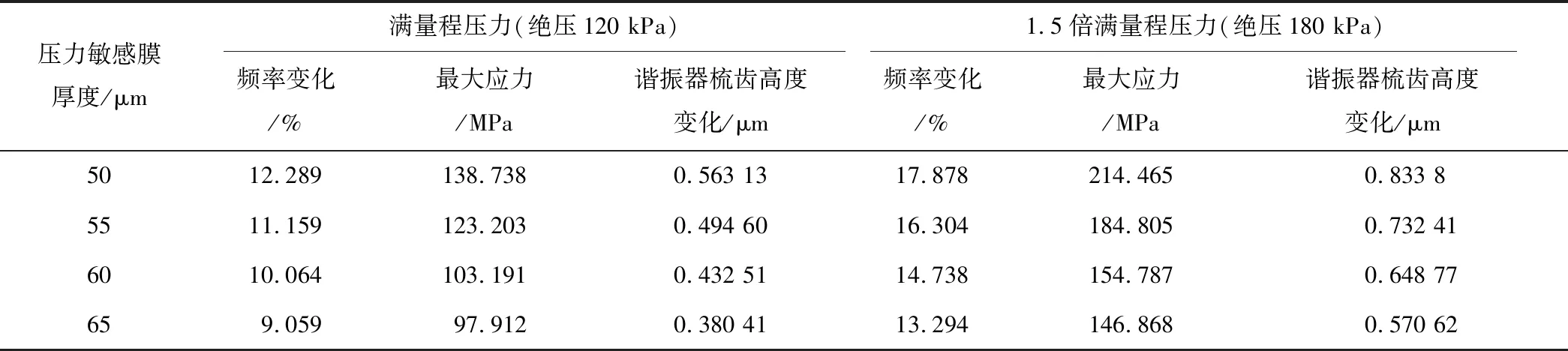
表2 不同敏感膜片厚度对应的传感器性能参数

图11为在120 kPa以及180 kPa压力作用下谐振器、硅岛和压力敏感膜复合结构的应力分布和变形图，其应力集中区域位于结构连接处，远小于单晶硅材料的强度极限，满足强度要求。如图12所示，为无压力载荷作用下传感器结构的前6阶模态振型及固有频率，其与谐振器的的仿真结果完全相符，工作模态仍为2阶模态，但是由于固定端结构会导致谐振梁弹性系数稍有变化，因此其各阶固有频率均略有下降。

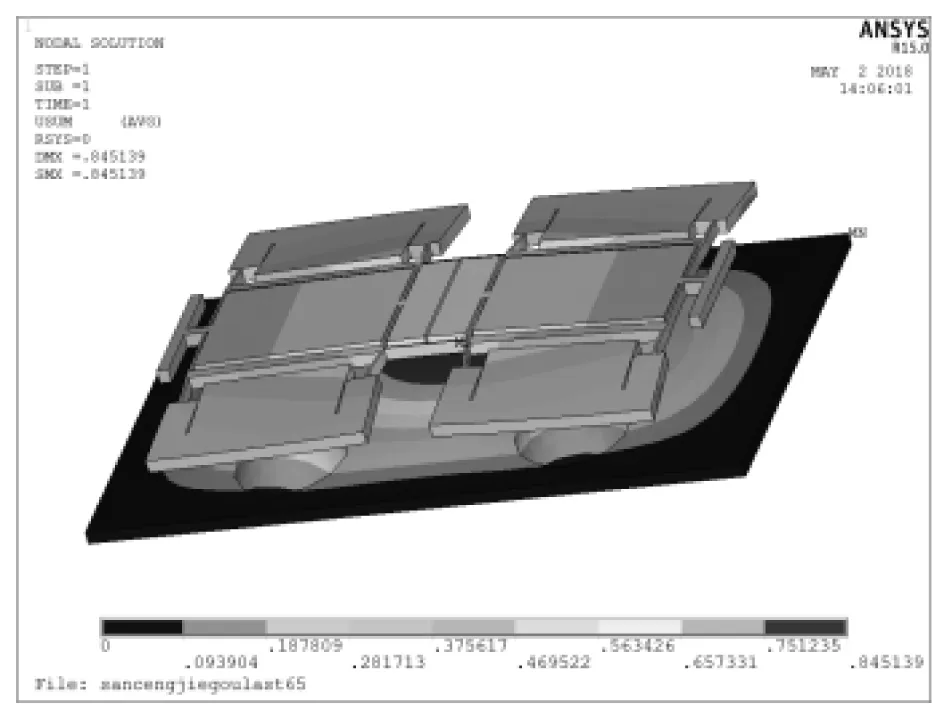
(a)120 kPa下变形图

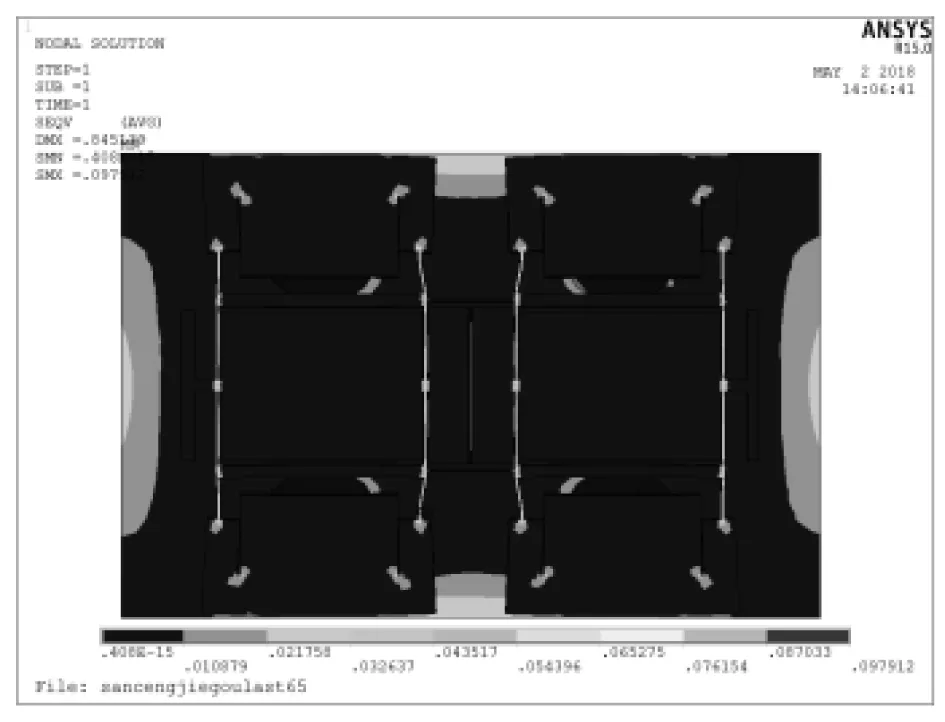
(b)120 kPa下应力分布

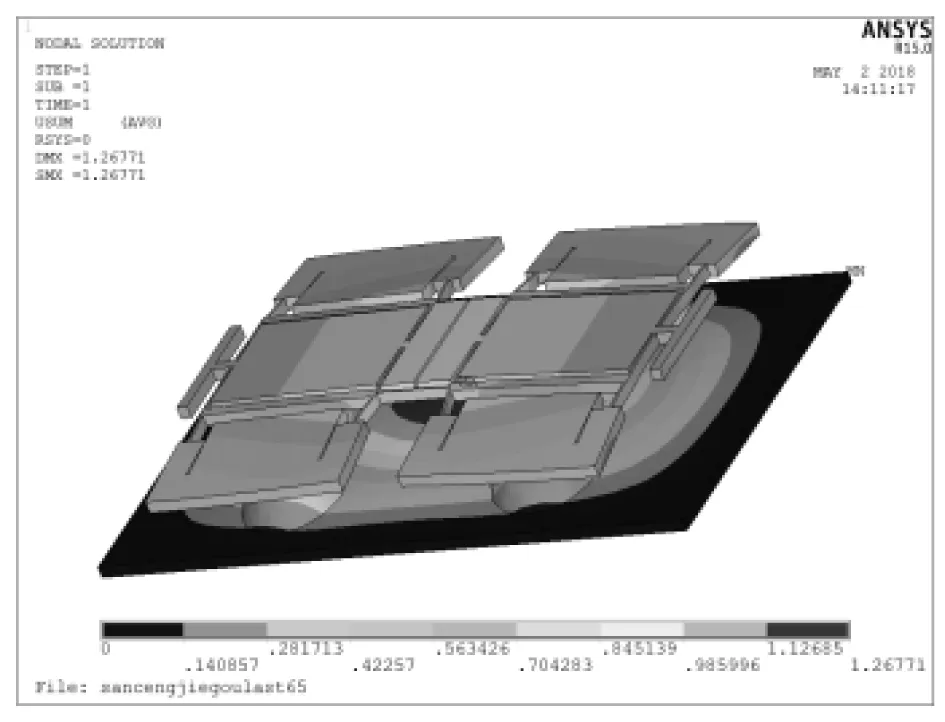
(c)180 kPa下变形图

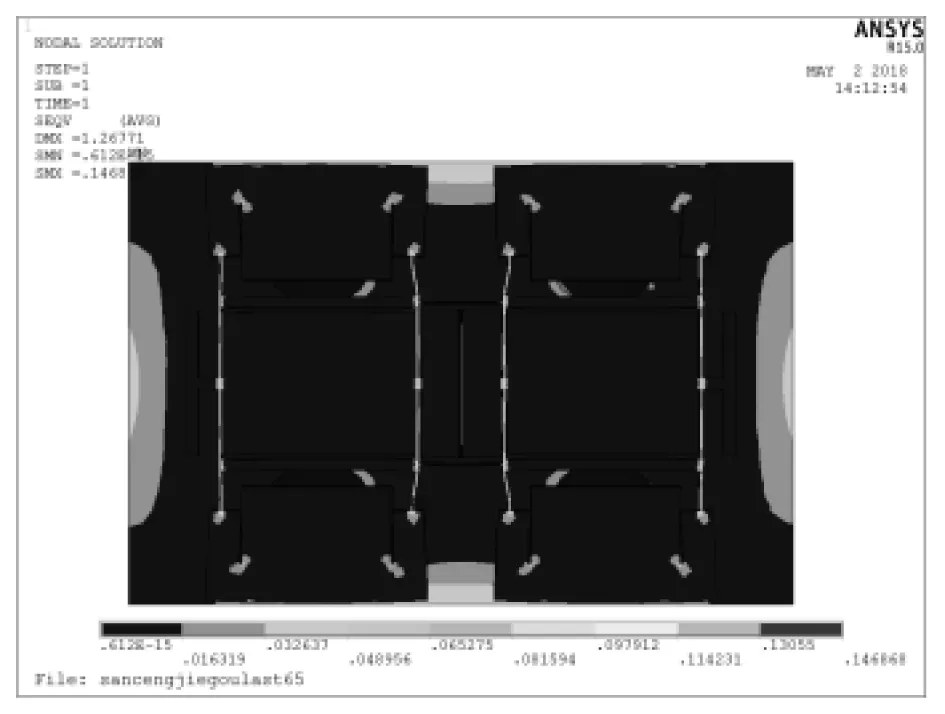
(d)180 kPa下应力分布

图11 120 kPa及180 kPa下硅微机械谐振压力传感器的应力分布及变形图

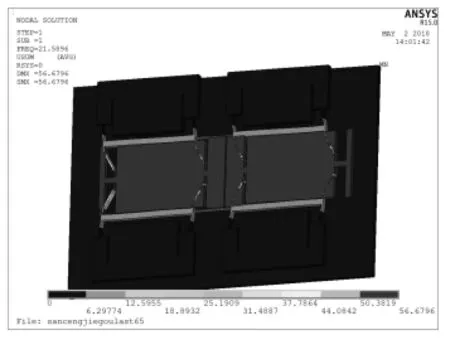
(a)1阶模态(21.590 kHz)

(b)2阶模态(24.010 kHz)

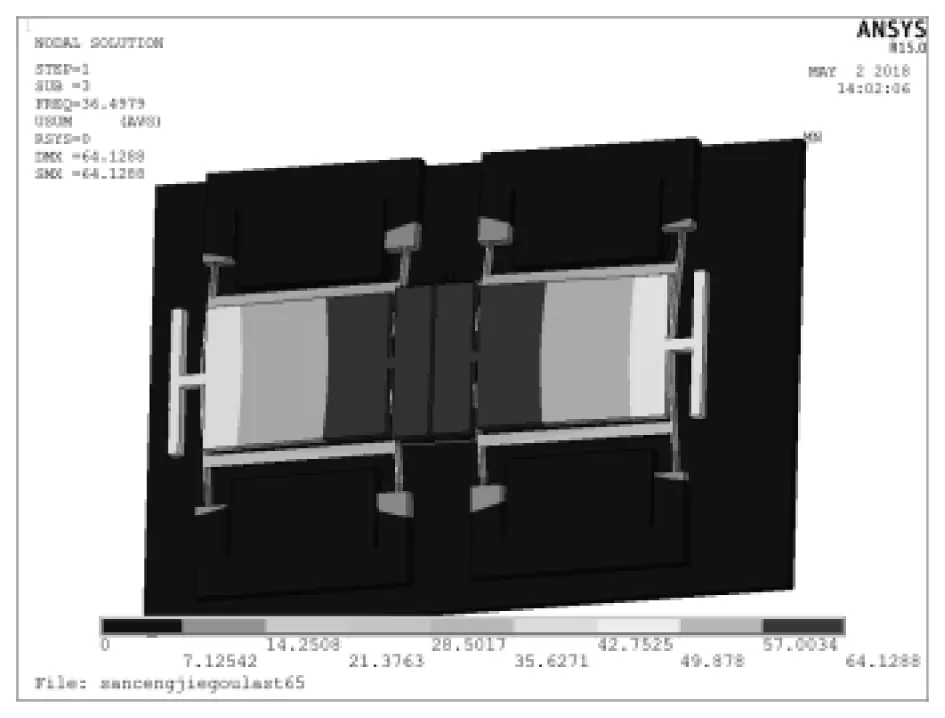
(c)3阶模态(36.498 kHz)

(d)4阶模态(40.749 kHz)

(e)5阶模态(59.812 kHz)

(f)6阶模态(68.259 kHz)

如图13所示ANSYS仿真得到了在不同外界压力下硅微机械谐振压力传感器的前6阶模态频率变化。可以看出在满量程压力范围内，谐振器可以稳定的工作在平行于压力敏感膜片的2阶面内动平衡振动模态，与相邻的模态保持了足够的频率间隔，满足设计目标。

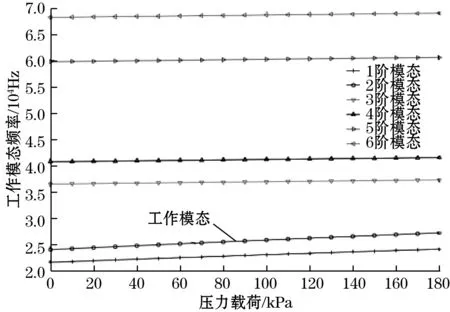
图13 压力载荷与传感器模态频率关系曲线

4 制备工艺

(1)备片：准备2块双面抛光SOI硅片，分别为厚度475 μm的第一SOI硅片和厚度380 μm的第二SOI硅片。

(2)刻蚀：在第一SOI硅片刻蚀325 μm高的硅岛和150 μm厚的压力检测敏薄膜区域，制得底层SOI晶圆，如图14(a)所示。

(3)硅-硅键合：采用硅-硅键合工艺将底层SOI晶圆与第二SOI硅片进行键合，在键合后形成的新的结构背部，生成氮化硅层以保护减薄工艺中的新结构底部，如图14(b)所示。

(4)去除第二SOI硅片以及中间埋氧层部分，剩下的顶层部分70 μm厚度作为谐振器结构层硅片，如图14(c)所示。

(5)一次光刻：对底层SOI晶圆的底部进行光刻，显影暴露出压力检测敏薄膜区域，再将底层SOI晶圆置入腐蚀槽中进行刻蚀，将压力检测敏薄膜区域的厚度刻蚀至65 μm。

(6)在谐振器结构层硅片上选择性掺杂固体硼扩散和氧化物掩膜以减小接触焊盘与传输路径的阻值，并在传输路径以及接触焊盘周围刻蚀绝缘槽，如图14(d)所示。

(7)二次光刻：光照图形转移至结构层硅片上获得谐振器、传输路线和接触焊盘区域，在真空封装密封环处刻蚀微槽，刻蚀完毕生长一层100 nm热氧化层以保护谐振器表面，如图14(e)所示。

(8)硅-硅键合：将盖帽硅层与结构层硅片键合，实现谐振器的真空封装；盖帽硅层底部设有与谐振器相匹配的盖帽硅凹槽，盖帽硅凹槽表面附有Ti吸气剂涂层；在接触焊盘相应位置的盖帽硅层作硅通孔，引出电信号，如图14(f)所示。

(9)顶部封装由电路芯片引线键合在封装衬底上，电路芯片采取倒装焊技术，利用填充工艺缓解热应力失配，键合后引线用环氧材料密封进行保护，并通过硅通孔实现与传感器之间的信号传输，完成三维混合集成封装，如图14(g)所示。

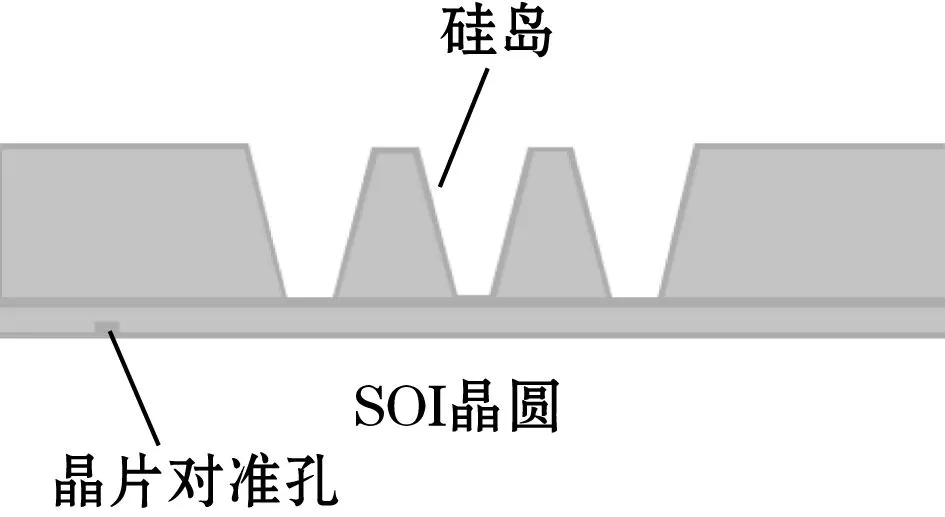
(a)刻蚀硅岛

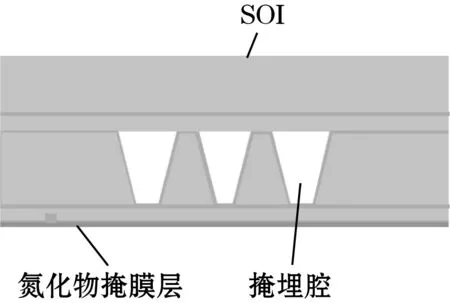
(b)键合

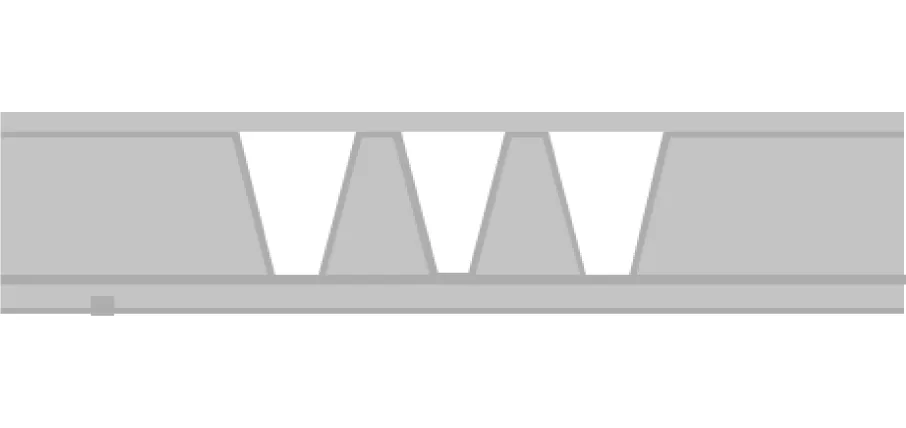
(c)去除SOI衬底硅和埋氧层

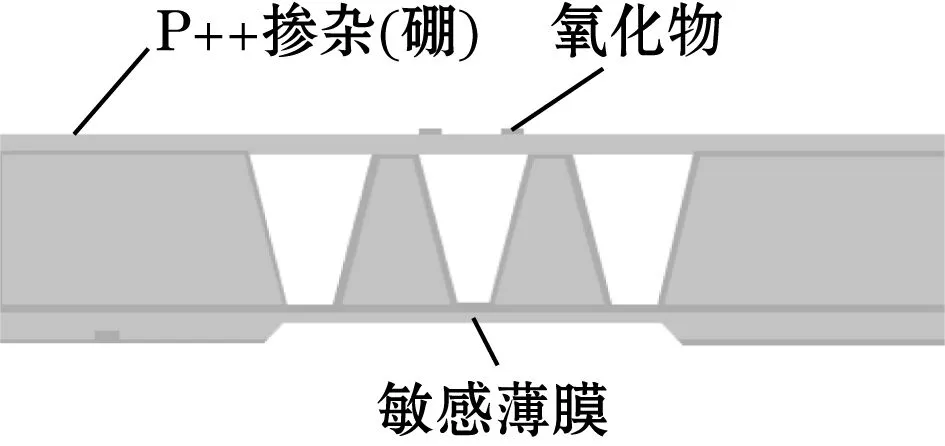
(d)掺杂

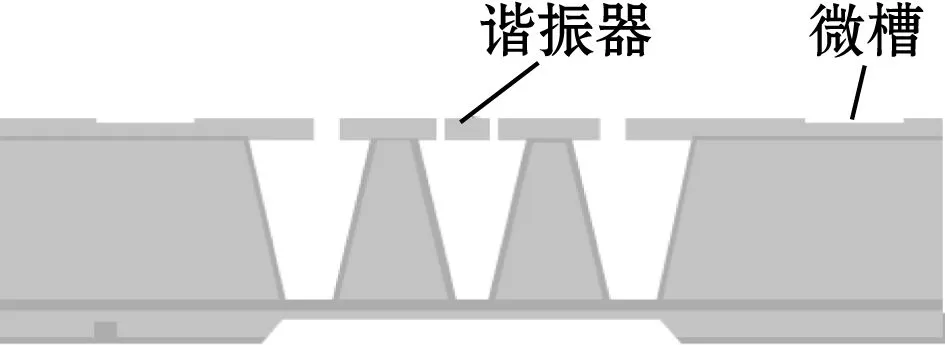
(e)刻蚀

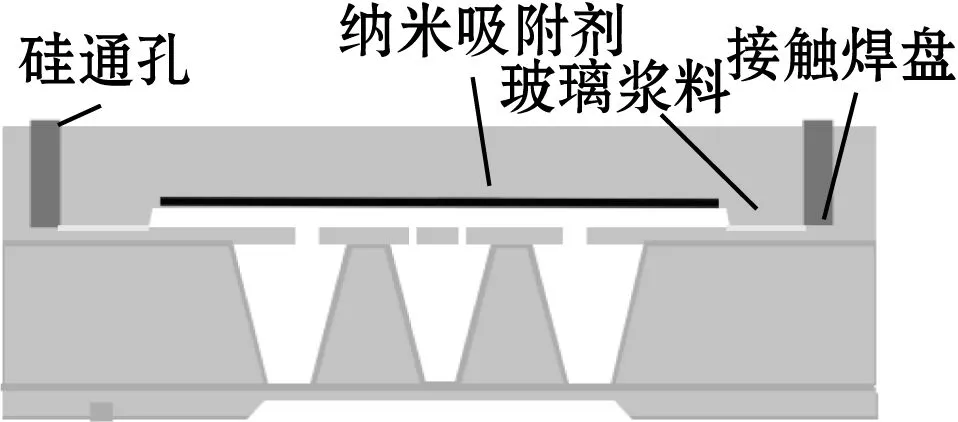
(f)真空封装

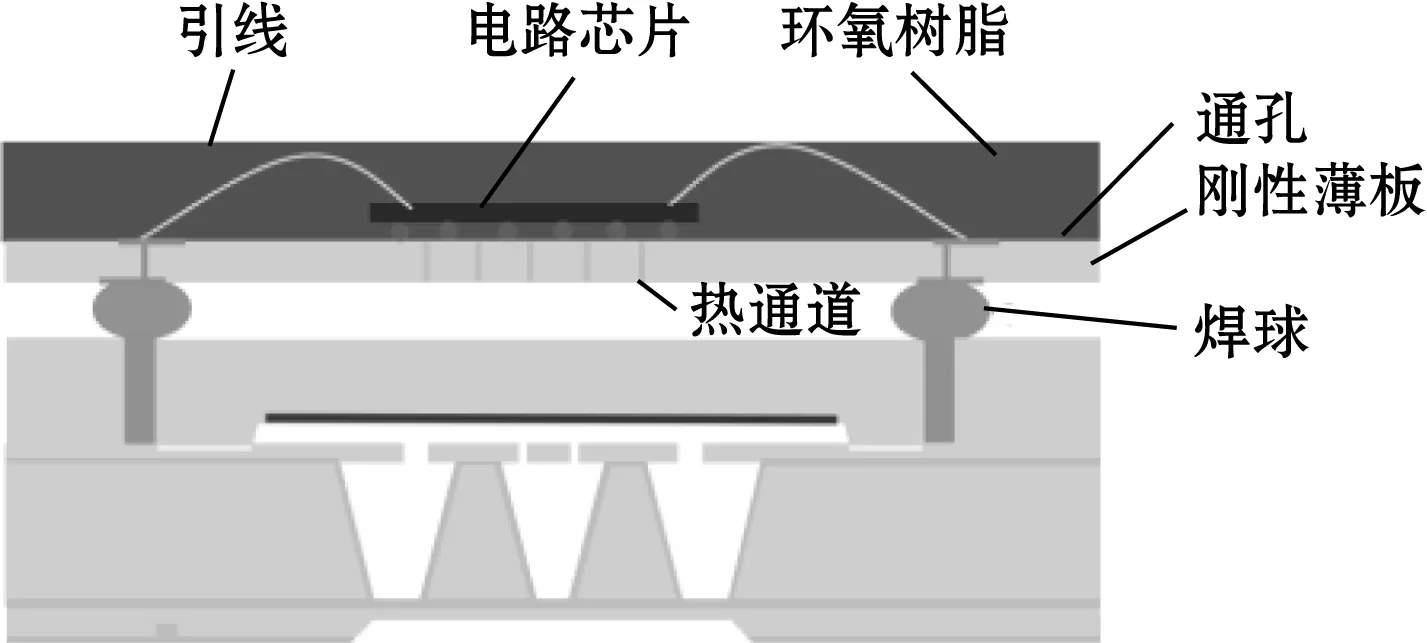
(g)三维集成混合封装

5 结论

本文基于SOI的加工工艺，通过理论分析和有限元仿真设计了谐振器的结构参数、压力敏感膜厚度和硅岛尺寸，通过硅-硅键合工艺完成传感器的真空封装，为抑制压力敏感膜片受压变形时谐振器的高度变化，在谐振器固定端设计桁架结构，仿真结果表明：在满量程压力下谐振器高度变化减小到约0.4 μm，保证驱动与检测的稳定性，降低闭环控制的难度，在0～120 kPa量程中具有高达18 Hz/kPa灵敏度，并基于TSV硅通孔技术实现硅微谐振式压力传感器与电路芯片的三维混合集成封装。