计数原理试题探源与应用易苏

■江苏省沭阳高级中学 易苏胜

加法计数原理和乘法计数原理是排列组合的基础，正确无误地理解两个原理是解决排列组合问题的前提。排列组合也是概率分布的基础，是高考必考的内容。但是排列组合问题却是非常容易出错的，既考验考生思维的缜密性，又考验考生临场的发挥能力。可以说这部分内容是获得高分路上的绊脚石，是让很多同学望而生畏的部分。

大家都知道考试总是来自于课本，但又高于书本的! 几乎每个问题都可以在书本上找到原型，都是从书本的例题或者练习题衍化而来的，所以学透书本知识，找到问题的源头，一定是不错的方法。

书本改编1(选修2-3P5 例3 改编)书架的第1层放有4 本不同的计算机书，第2层放有3本不同的文艺书，第3层放有2 本不同的体育书。从书架中任取1 本书，则不同取法的种数为____。

解析：从书架上任取1 本书，有3 类方法：第1类方法是从第1层取1本计算机书，有4种方法；第2类方法是从第2层取1 本文艺书，有3种方法；第3类方法是从第3层取1本体育书，有2 种方法。根据分类加法计数原理，不同取法的种数是N=m1+m2+m3=4+3+2=9。

书本改编2(选修2-3P19例4改编)用数字1，2，3，4，5组成的无重复数字的四位偶数的个数为____。

解析：先排个位，有种排法；再排剩下的三位，有种排法。故共有(种)排法。

书本改编3(选修2-3P28A 组第14 题改编)从5 名女同学和4 名男同学中选出4人参加演讲比赛，男、女同学分别至少有1名，则不同的选法有____种。

解析：

书本改编4(选修2-3P28B 组第2题改编)现有4 种不同颜色要对如图1所示的四个部分进行着色，要求有公共边界的两块不能用同一种颜色，则不同的着色方法共有( )。

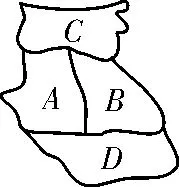
图1

解析：如果先给C 块着色，有4种结果；再给A 块着色，有3种结果；再给B 块着色，有2种结果；最后给D 块着色，有2种结果。由分步乘法计数原理知，不同的着色方法共有4×3×2×2=48(种)。

书本改编5(选修2-3P28A 组第15 题改编)某工厂将甲、乙等五名新招聘的员工分配到三个不同的车间，每个车间至少分配一名员工，且甲、乙两名员工必须分到同一个车间，则不同分法的种数为____。

解析：若甲、乙分到的车间不再分人，则分法有若甲、乙分到的车间再分一人，则分法有所以满足题意的分法共有18+18=36(种)。

创新应用1在连接正八边形的三个顶点而成的三角形中，与正八边形有公共边的三角形的个数为____。(用数字作答)

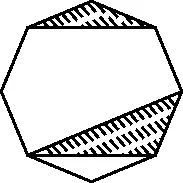
图2

解析：与正八边形有公共边的三角形共有两类，如图2所示：第一类，有一条公共边的三角形共有8×4=32(个)；第二类，有两条公共边的三角形共有8个。由分类加法计数原理知，满足题意的三角形共有32+8=40(个)。

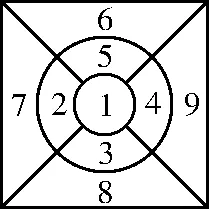
图3

创新应用2如图3，图案共分9个区域，有6种不同颜色的涂料可供涂色，每个区域只能涂一种颜色的涂料，其中2 和9 同色、3和6 同 色、4 和7 同 色、5 和8 同色，且相邻区域的颜色不相同，则涂色方法有( )。

A.360种 B.720种

C.780种 D.840种

解析：由题意知2，3，4，5 的颜色都不相同，先涂1，有6种方法，再涂2，3，4，5，有种方法，故共有6·=720(种)。

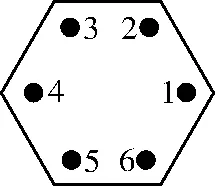
图4

创新应用3工人在安装一个正六边形零件时，需要固定如图4所示的六个位置的螺栓。若按一定顺序将每个螺栓固定紧，但不能连续固定相邻的2 个螺栓，则不同的固定螺栓方式的种数是_____。

解析：在六个螺栓中随机选择一个固定，有6种不同的选法，不妨选择以位置1 的螺栓为例，选择一个与1 不相邻的位置的螺栓固定，此时有两类：位置4或位置3，5，当选择位置4时，第三个固定的螺栓位置可以为2，6中的一个，第四个固定的螺栓的位置相应有两种情况，此时第五个固定和第六个固定的位置相应确定；当选择位置3，5时，不妨以位置3 为例，此时第三个固定的螺栓的位置可以为5，6中的一个，若第三个固定的位置为5，则第四个固定的位置只有2一种选择，第五个固定的位置有两种选择，第六个固定的位置相应确定，若第三个固定的位置为6，则第四个固定的位置只能为4，第五个固定的位置只能为2，第六个固定的位置相应确定。综上所述，不同的固定螺栓方式的种数为6×[2×2+2×(2+1)]=60。

创新应用4从5男3女共8名学生中选出队长1人，副队长1人，普通队员2人组成4人服务队，要求服务队中至少有1 名女生，则不同的选法共有_____种。(用数字作答)

解析：第一类，先选1女3男，有30(种)，这4 人中选2 人作为队长和副队长有=12(种)，故有30×12=360(种)；第二类，先选2女2男，有(种)，这4人中选2人作为队长和副队有=12(种)，故有30×12=360(种)；第三类，先选3女1男，有，这4人中选2人作为队长和副队有=12(种)，故有5×12=60(种)。根据分类计数原理知，不同的选法共有360+360+60=780(种)。

创新应用5某省现行的高考招生制度规定：除语、数、英之外，考生须从政治、历史、地理、物理、化学、生物、技术这7门高中学考科目中选择3 门作为高考选考科目，成绩计入高考总分。已知报考某高校A、B 两个专业各需要1门科目满足要求即可，A 专业：物理、化学、技术；B 专业：历史、地理、技术。考生王某今年打算报考该高校这两个专业的选考方式有_____种。(用数字作答)

解析：依题意得，当考生选择技术时，两个专业均可报考，再从剩下的6 门科目中选择2门即可，方法有当学生不选技术时，可以从物理、化学中选择1 门科目，再从历史、地理中选1 门科目，最后从政治、生物中选择1门科目，有2×2×2=8(种)方法；当学生同时选物理、化学时，还需要选择历史、地理中的1 门科目，有2 种选择；当学生同时选择历史、地理时，需要从物理、化学中再选择1 门科目，也有2 种方法。根据分类计数原理知，满足题意的选考方式共有15+8+2+2=27(种)。

排列组合问题往往以实际问题为背景，考查排列数、组合数、分类分步计数原理。应用两个计数原理的难点在于明确分类还是分步。在处理具体的应用问题时，首先必须弄清楚“分类”与“分步”的具体标准是什么。选择合理的标准处理事情，可以避免计数的重复或遗漏。分类要做到“不重不漏”，分类后再分别对每一类进行计数，最后用分类加法计数原理求和，得到总数；分步要做到“步骤完整”，完成了所有步骤时恰好完成任务，步与步之间要相互独立，分步后再计算每一步的方法数，最后根据分步乘法计数原理，把完成每一步的方法数相乘，得到总数。

事实上，平时遇到的问题大多都是混合问题，这个时候一般是先分类再分步。在分析和解题问题的过程中可以恰当地画出示意图或者树状图，使问题的分析更直观、清楚，便于探索规律。常言道：“世上无难事，只怕有心人!”相信在勇攀高峰的道路上，只要一步一个脚印，定能披荆斩棘，成功到达终点。