气膜孔图像对焦评价函数的实验研究

毕 超 郝 雪 李剑飞 房建国

(1.北京航空精密机械研究所 精密制造技术航空科技重点实验室，北京 100076； 2.中国航发南方工业有限公司，株洲 412002)

1 引 言

在航空领域中，发动机是飞机最为关键和复杂的部件，它的性能优劣和安全性等级，直接关系到飞机的整体性能[1]。在发动机的工作循环中，涡轮叶片不仅要承受热负荷、气动负荷和机械负荷，还要承受高温高压燃气流的强烈冲击[2]。在这样恶劣的工作环境中，为了确保涡轮叶片能够长期可靠服役，在应用耐高温材料和热障涂层的基础上，还必须采用先进的气膜冷却技术[3]，即在涡轮叶片的叶身型面上设计和加工出众多孔径小、深径比大、轴线角度复杂的冷却气膜孔(以下简称“气膜孔”)。

研究表明：气膜孔的孔径、分布位置和轴线角度等形位参数会对涡轮叶片在高温高压下的机械性能和冷却效果产生重要影响[4]。因此，为了使涡轮叶片达到最佳的冷却效果，必须对气膜孔的实际几何技术状态实施监控。

为了完成批量气膜孔的制造质量检测与评价，本文基于工业影像测头与多轴联动装置，设计并搭建了非接触式的四轴视觉坐标测量系统，通过获取被测气膜孔的图像数据来实现其形位参数的视觉测量。在测量过程中，为了能够精确获取被测气膜孔的出口孔径和分布位置，需要使工业影像测头正确对焦于气膜孔的出口表面，此时才能够采集到最清晰的气膜孔图像以进行后续的图像处理和参数计算。

根据成像原理，对于位于一定距离处的被测物体，改变其与视觉系统之间的相对位置关系，都会使其到达一个成像的最佳位置，即对焦位置[5]。当被测物体处于对焦位置时，所采集到的图像最清晰，细节也最丰富；而当被测物体偏离对焦位置时，系统处于离焦状态，会带来细节丢失和图像模糊，增大后续图像处理的难度和不确定性，因而离焦会对视觉系统的性能产生不利影响。

因此，在实际应用中，需要对视觉系统进行调焦，即通过调整使其成像状态由离焦到对焦的过程[6]。在众多种类的调焦方式中，通过对焦评价函数计算出图像序列的清晰度(sharpness)并利用正确对焦时图像最清晰、细节最丰富的这个特性进行调焦，具有可操作性强、易于实现自动化等优点，因而被广泛应用于各类光学成像系统中[7]。王健等通过采用高通和带通两个滤波器对传统Brenner对焦评价算法进行了改进，克服了阈值对传统Brenner算法评价结果的影响，在满足单峰性和无偏性的前提下，提高了灵敏度并且降低了运算次数[8]。易怀安等提出了一种基于图像清晰度评价的磨削表面粗糙度检测方法，采用了熵函数评价算法和基于色彩相关性的彩色图像清晰度评价算法分别构建清晰度与粗糙度之间的关系模型，并进行了试验验证[9]。张俊杰等基于微型精密零件的成像测量方法，从8种灰度图像清晰度评价算法中计算出了适用于微型零件光学影像测量的评价算法，并建立了综合清晰度评价模型[10]。

为了实现高压涡轮叶片上的气膜孔形位参数的精确测量，本文在视觉测量和多轴联动控制的基础上，设计并搭建了一套非接触式的四轴视觉坐标测量系统。对于系统调焦过程中的对焦评价函数问题，基于被测叶片及气膜孔的成像特性开展了有针对性的实验研究。首先，详细分析了对焦评价函数所应满足的特性、要求以及灰度梯度函数、频域函数、信息学函数和统计学函数的优缺点；然后，选取5种具有代表性的灰度梯度函数进行实验验证，通过实验获得了它们的函数曲线，并进行归一化处理和比较分析，从而选择出了最适用的对焦评价函数，而后对其进行了重复性验证，从而为后续的图像处理奠定了坚实基础。

2 对焦评价函数

2.1 选取原则

基于数字图像的被动调焦方式，在工业影像测头的焦距和放大倍数均不改变(定焦定倍)的情况下，控制测量系统按照设定的步长获取被测物体的一系列图像(图像序列)，而后通过对焦评价函数来计算每幅图像的清晰度，以此作为指标来判断系统的调焦状态和对焦位置，从而寻找到成像最清晰的位置，实现调焦[11]。在这个过程中，如何评价图像的清晰程度，即采用何种对焦评价函数来计算图像的清晰度数值，是系统进行正确调焦的关键。

本文的研究对象为涡轮叶片上的气膜孔，具有一定的特殊性。一方面，涡轮叶片的材料大多为高温合金，表面粗糙度较低，因而叶片外观大多富有光泽且具有反光特性；另一方面，涡轮叶片表面的结构组织排列属性及热障涂层等也会使其表面呈现出特定的纹理和细节特征，不同于常规的工业产品。因此，要使工业影像测头瞄准被测气膜孔的出口表面，即实现对分布于叶身型面上的气膜孔的自动对焦，就需要有针对性地开展对焦评价算法的研究，以构建或选取出最适用的对焦评价函数。

一般情况下，对于特定的被测物体和视觉系统来说，一个适用的对焦评价函数应满足如下要求，其函数曲线也会呈现出如图1所示的形态特征。

(1)单峰性。要求对焦评价函数的曲线呈现单峰特性，避免出现双峰或者多峰，即在调焦范围内只有一个极大值点，而没有其他局部峰值的干扰[12]。同时，极大值点两侧的曲线均应是单调的，这样才能够反映出系统的离焦极性[13]。

(2)无偏性。要求对焦评价函数得到的结果与理论对焦位置之间不存在偏差，即极大值点或峰值所对应的成像位置就应为对焦位置，只有在此位置处才能够采集到最清晰的图像，这样才能够确保调焦过程的正确性。

(3)灵敏度高。灵敏度用于表征图像的细微变化对于对焦评价函数的数值变化的影响程度。灵敏度越高的对焦评价函数，其正确区分对焦和轻微离焦的能力越强，因而对焦精度也就越高。如图1所示，极大值点两侧的函数值变化越快，且波峰越尖锐，则其灵敏度就越高。

(4)稳定性好。对焦评价函数要具有足够的鲁棒性和抗噪声干扰能力。当图像中存在噪声时，函数曲线要能够维持基本的形状特征而不产生较大的失真。

(5)计算量小。计算量小的对焦评价函数，可以达到较高的计算效率，因而易于实现系统的实时、快速调焦。

在图1中，对焦评价函数值即可用于表征图像的清晰度，从而判定系统的调焦状态。在上述对焦评价函数的选取原则中，单峰性和无偏性决定了算法的正确性[14]，因而任何用于图像清晰度计算的对焦评价函数都首先必须满足这两个要求，但同时也应兼顾到其他几个选取原则。

图1 对焦评价函数曲线的形态特征Fig.1 Morphological character of the focusing evaluation function curve

2.2 对焦评价函数类型

对于特定的视觉系统而言，由对焦评价函数计算得到的图像清晰度，能够在一定程度上反映出系统的成像状态，即对焦或离焦。在对焦状态下，图像细节清晰、内容丰富，在空域上表现为相邻像素的特征值(如灰度、颜色等)变化较大，在频域上表现为高频分量较多；而在离焦状态下，像素互相重叠、成像轮廓平滑、部分细节丢失，造成图像模糊。利用这些特性，可以构造了多种对焦评价算法与函数，实现对图像清晰程度的判别。

目前，常用的对焦评价函数主要有灰度梯度函数、频域函数、信息学函数和统计学函数四大类。其中，灰度梯度函数大多基于各类空域边缘检测算子，形式较为简单且易于实现，图像经过处理后得到的量值能够反映出图像的清晰程度，并且可以通过微分来获取更多细节信息；频域函数的计算量较大，一般不适用于快速计算与实时测量；信息学函数随着图像内容的不同而易出现较大波动，甚至会出现峰谷倒置这样完全相反的结果；统计学函数的对焦精度较低，实际应用不多。因此，灰度梯度函数作为一种有效的对焦评价函数，在光学系统的自动对焦方面得到了最广泛的应用。根据上述分析，本文选用灰度梯度函数作为系统中气膜孔图像的对焦评价函数。

一般说来，灰度梯度函数是利用对像素灰度值的特定处理来表征图像的清晰程度。在实际应用中，大多采用边缘检测算子来构建灰度梯度函数，这是因为图像的清晰程度与其边缘特征之间有着非常密切的关系。具体说来，当成像清晰时，图像边缘特征处的灰度阶跃变化较大，使不同灰度区域之间的接线较为清晰；而当成像不清晰时，图像边缘特征处的灰度阶跃变化较小，造成不同的灰度区域连成一片，导致图像模糊。因此，可以利用图像边缘特征处的灰度阶跃变化程度来表征图像的清晰度。从这个意义上来说，可以基于不同种类的边缘检测算子来构建出不同的灰度梯度函数作为对焦评价函数，例如Brenner梯度函数、Tenengrad梯度函数、Laplacian梯度函数、方差函数和能量梯度函数等。

(1)Brenner梯度函数

该函数以Brenner边缘检测算子为基础，只计算图像中相差两个单元的两个像素之间的灰度值差。对于一幅像素数目为M×N的灰度图像f，其Brenner梯度函数的定义为

(1)

式中：D(f)——图像f的清晰度计算结果；f(x,y)——像素(x,y)的灰度值；x、y——像素在图像f中的坐标；T——设定的边缘检测阈值。

(2)Tenengrad梯度函数

该函数以Sobel边缘检测算子为基础，分别提取图像在水平和垂直方向上的灰度梯度，其定义如下

(2)

式中：Gx(x,y)和Gy(x,y) ——分别为像素(x,y)处的水平和垂直方向上的Sobel边缘检测算子的卷积。

一般情况下，Sobel边缘检测算子采用如下的卷积模板来检测图像的边缘特征

(3)

(3)Laplacian梯度函数

该函数与Tenengrad梯度函数类似，只需要用Laplacian算子来替代Sobel算子即可，其定义为

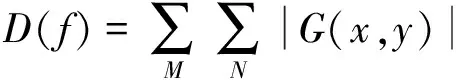
(4)

式中：G(x,y)——像素(x,y)处的Laplacian算子的卷积。一般情况下，Laplacian边缘检测算子采用如下的卷积模板来检测图像的边缘特征

(5)

(4)方差函数

该函数取各个像素的灰度值与平均灰度之差的平方作为对焦评价函数，其定义如下

(6)

式中：u——当前图像f的平均灰度值。

(5)能量梯度函数

该函数应用相邻像素的灰度差分来计算一个像素的灰度梯度，其定义如下

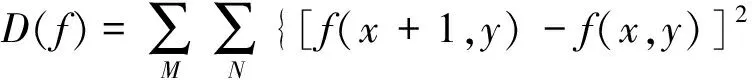
(7)

3 系统组成

根据高压涡轮叶片上的气膜孔特征的分布特点与测量需求，应用三坐标测量机、工业影像测头、回转工作台和叶片夹具等搭建了非接触式的四轴视觉坐标测量系统，如图2所示，从而将三坐标测量机的移动范围大、定位精确和通用性强等优点与工业影像测头的非接触、信息丰富和应用灵活等优点结合在一起[15]，并且增加了回转工作台(第四轴)以用于被测叶片的转位。该测量系统的运动机构由X、Y和Z三个直线轴和一个回转轴构成。其中，X、Y和Z轴集成在一起，由三坐标测量机实现；而回转轴单独布置，由回转工作台实现；被测高压涡轮叶片则通过叶片夹具固定在回转工作台上。

图2 四轴视觉坐标测量系统Fig.2 4-axis vision coordinate measuring system

工业影像测头由工业相机、镜头与光源等组成，如图3所示。其中，工业相机选用大恒图像生产的水星MER系列工业数字相机，该型相机采用全局曝光的Sony IMX252 CMOS传感器，其分辨率为2048×1536，像素尺寸为3.45μm×3.45μm。为了配合该型工业相机的使用，选用了日本MORITEX公司的MML-ST系列工业远心镜头，该型镜头具有高对比度、高分辨率和低失真度的特征，其放大倍率为3×，工作距离为108.3mm，景深为0.44mm。

图3 工业影像测头Fig.3 Industrial CCD

4 实验与结果分析

为了从上述5种灰度梯度函数中选择出最适用于本文所搭建的四轴视觉坐标测量系统的对焦评价函数，以实现气膜孔形位参数的精确测量，选取某个高压涡轮叶片作为被测物，通过实验对上述5种典型算法进行比较和分析，实验现场如图4所示。

图4 实验现场Fig.4 Experimental scene

在实验过程中，首先，控制回转工作台使叶片上的待测气膜孔朝向工业影像测头，并通过X、Y和Z轴的运动使工业影像测头对准被测气膜孔，使整个气膜孔处于工业影像测头的视场范围中，而后调节照明光源到适当的亮度水平，使图像中的细节特征得到最大限度的展示且不出现过多的亮斑；然后，控制测量系统的Y轴带动工业影像测头移动，从而调整被测气膜孔与工业影像测头之间的相对位置关系，移动距离为0.4mm(包含对焦位置在内)，同时按照0.01mm的步长采集被测气膜孔的图像序列，因而整个过程会采集到41幅图像，这些图像各自具有不同的离焦程度，因而呈现为由模糊到清晰再到模糊的变化趋势，如图5所示为此过程中所采集到的两幅图像；最后，对图像序列进行中值滤波，而后分别带入到上述5种灰度梯度函数中计算每幅图像的清晰度数值，并绘制出对应的对焦评价函数曲线。

图5 采集到的气膜孔图像Fig.5 Images of the film cooling hole

为了便于统一比较和分析各种算法的性能，本文对5种对焦评价函数的输出结果进行了归一化处理，并且以图像序列中的序号为横轴，以对焦评价函数输出结果的归一化值为纵轴，将归一化后的5种函数曲线均画在同一个坐标系中，如图6所示。

图6 5种对焦评价函数的曲线Fig.6 Curves of the 5 kinds of focusing evaluation functions

从图6中可以看出，方差函数曲线几乎没有呈现出对焦评价函数曲线应有的形态特征，出现了形状畸变和倒置的现象，因而对于被测气膜孔的图像序列来说，方差函数基本失效而不可用，这说明成像目标的表面特征(如表面粗糙度、细节和纹理等)对方差函数的影响很大，因而不适用于本文的应用场景。

而其他函数的曲线均呈现出了应有的样式和特性，进一步分析如下：首先，这4种对焦评价函数的曲线均具有较为平滑的形状，只有一个极大值点，并且在极大值点两侧均是单调的，符合单峰性要求；其次，Brenner梯度函数的极大值点所对应的图像序号为26，Tenengrad梯度函数为24，Laplacian梯度函数为26，能量梯度函数为26，因而除了Tenengrad梯度函数存在些许偏差之外，其他函数判别出来的对焦位置均一致，所对应的Y轴坐标为298.3203mm，且与实际情况相吻合，因而Tenengrad梯度函数在无偏性方面有所欠缺；再次，相比于Brenner梯度函数和能量梯度函数，Laplacian梯度函数的峰顶宽度较窄，曲线更加陡峭，因而灵敏度最高，易于实现更精确的调焦。而在计算量方面，在前文的公式描述中可以看出，Brenner梯度函数、Tenengrad梯度函数、方差函数和能量梯度函数均采用了平方求和的计算形式，而Laplacian梯度函数则为绝对值求和，因而在这5种对焦评价函数中，Laplacian梯度函数的计算形式简单且计算量最小，将更易于实现系统的实时、快速调焦。

综合上述分析，本文选择Laplacian梯度函数作为系统的对焦评价函数。为了进一步验证该函数的应用性能和效果，进一步将采集图像序列的步长设置为0.005mm，而移动距离保持不变，而后将采集到的81幅图像经中值滤波后带入到Laplacian梯度函数中计算每幅图像的清晰度，连续进行5次实验，所得到的各次函数曲线如图7所示。

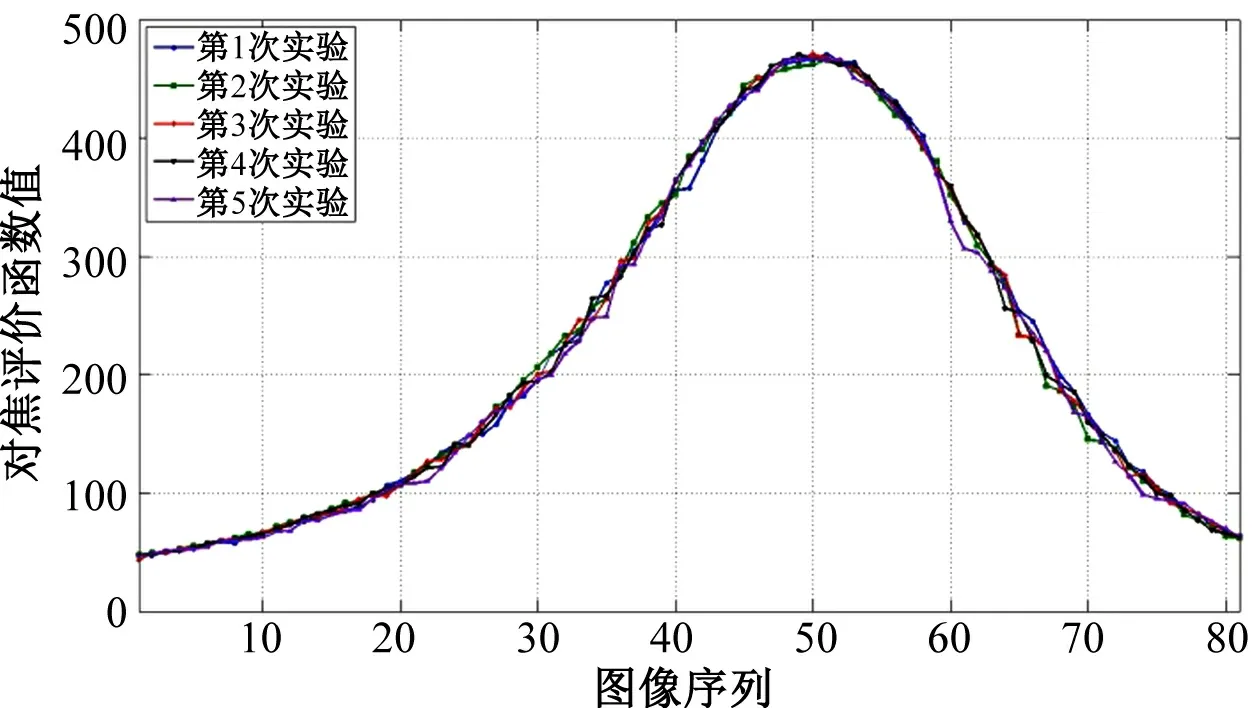
图7 Laplacian梯度函数曲线Fig.7 Curve of the Laplacian gradient function

从图7中可以看出，在调焦范围内，Laplacian梯度函数曲线呈现出了良好的重复性，并且极大值点所对应的图像序号均为50，而该幅图像在各次实验中所对应的Y轴坐标分别为298.3173mm、298.3148mm、298.3133mm、298.3133mm和298.3128mm，平均值为298.3143mm，标准差为0.0018mm，重复性小于0.005mm，并且与前文的实验结果相吻合。同时，这也进一步说明，在图像中普遍存在随机噪声的情况下，Laplacian梯度函数具有一定的抗噪声影响的能力，稳定性良好，从而使各次实验的对焦评价函数值没有出现较大程度的偏离，这就确保了各次实验曲线能够保持形状的一致性。

因此，将Laplacian梯度函数作为本文所搭建的四轴视觉坐标测量系统的对焦评价函数，能够正确判别出被测气膜孔的对焦位置，且对焦重复性小于0.005mm，可以满足气膜孔形位参数的检测要求。如图8所示为对焦位置处的气膜孔图像的边缘提取与圆周拟合结果，从而为气膜孔的孔径与坐标位置等形位参数的精确提取与计算奠定了坚实基础。

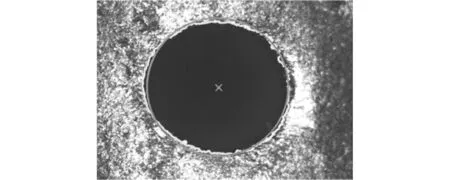
图8 被测气膜孔的图像处理Fig.8 Image processing result of the measured film cooling hole

5 结束语

在所设计和搭建的四轴视觉坐标测量系统中，为了使工业影像测头能够正确对焦于被测气膜孔的出口表面，本文采用了基于数字图像的被动调焦方式，并重点开展了对焦评价函数的实验研究。采用某个高压涡轮叶片作为被测物，分别对Brenner梯度函数、Tenengrad梯度函数、Laplacian梯度函数、方差函数和能量梯度函数这5种具有代表性的灰度梯度函数进行了考察，并根据对焦评价函数所必须具备的特性进行了比较和分析，最终确定应用Laplacian梯度函数作为测量系统的对焦评价函数，并且对其进行了重复性验证。Laplacian梯度函数具有良好的单峰性和无偏性，灵敏度较高，并且呈现出良好的重复性，能够正确判别出被测气膜孔的对焦位置，且对焦重复性小于0.005mm，可以满足气膜孔形位参数的检测要求，从而为气膜孔专用检测设备的研制和开发提供了一项技术支撑。