单目视觉三维运动位姿测量方法研究

袁 媛 刘 柯 孙增玉 高 越 刘 华

(北京航天计量测试技术研究所，北京100076)

1 引 言

视觉测量技术具有现场检测实时性、非接触测量等诸多优点，其研究重点是物体的几何尺寸及物体在空间中的位置、姿态等的测量。单目视觉的主要原理是应用单台摄像机，对单张位姿信息图像进行拍摄，通过图像处理得到特定信息，用于运动目标的位姿位置轨迹解算[1,2]。

单目视觉测量系统在现场实时测量中非常便于应用，且测量范围大、标定步骤少。此外，单目视觉还可修正双目视觉中测量视场范围小、视觉传感器之间立体匹配困难等缺点，因而近年来这方面的研究较为活跃。然而，如何准确快速的从预先标定好的摄像机拍摄的一帧图像中，利用空间点和图像点间的几何关系，解得摄像机与目标物体之间的位姿关系，一直是单目视觉测量技术的研究重点。目前，基于特征点的单目视觉位姿求解方法研究较多，又称为PnP问题，即在相机内参已知的情况下，利用待测目标上已知空间位置关系的一组特征点，来确定与摄像机的相对位置和姿态。PnP问题是机器视觉领域的一个经典问题，在航天器交会对接位姿测量、无人机姿态测量、目标跟踪等方面有很多重要的应用[3～5]。

本文在现有技术的基础上，对基于点特征的单目视觉解算算法进行研究，提出了一种基于5个编码特征点的单目视觉解算算法，该算法使用不共面五个编码特征点，利用大靶面高分辨率相机采集运动物体位姿图像，利用目标物体上编码特征点间的几何约束关系，通过正交迭代解算完成目标的位姿测量。

2 单目视觉位姿测量原理

单目视觉位姿测量原理，即采用单相机采集到的物体位姿图像，进而解算得到目标坐标系与摄像机坐标系间的三维六自由度位姿参数。视觉测量的本质是利用图像上已知的二维信息求解出物体的三维信息的过程，相机的成像模型是视觉测量的基础。其中，透视成像模型应用较为广泛，它可以简单的描述为：所有成像光线都通过光心，并且物点、像点、光心三点共线。透视成像模型由三维空间到图像平面的透视投影变换所给出，在成像过程中，需要选择一个基准坐标系，该坐标系定义为世界坐标系(Ow-xwywzw)，符合右手坐标系；以光心Oc为原点定义相机坐标系Oc-xcyczc，其中，Xc轴取图像坐标沿水平增加的方向，Yc轴取沿竖直增加的方向，Zc轴的方向平行于摄像机光轴。

设点P在世界坐标系下坐标为(xw,yw,zw)，在相机坐标系下的坐标为(xc,yc,zc)，相机的外参数模型表征了世界坐标系与相机坐标系的关系，可用公式(1)的外参矩阵表示：

(1)

式中：cMw——外参矩阵，R——相机坐标系与目标坐标系间的旋转矩阵；t——相机坐标系与目标坐标系间的平移变换矩阵。

通过目标物体上一组坐标已知的编码特征点坐标，由公式(1)经位姿解算求解得到两坐标系之间的R、t矩阵。

3 实施途径

3.1 编码标志点的设计

本文采用环形编码特征点，如图1(a)所示。它由中心圆和中心圆环两部分组成，中心圆环等分为10个编码环带，其结构形式如图1(b)所示。每份有亮带和暗带两种状态，对应二进制码为1和0，以任一环带作为起始位，逆时针循环选取得到最小15位二进制数，作为此编码特征点的编号，可作为唯一性标识，进而进行编码特征点的精确识别和提取。

(a)编码特征点实际图像 (b)编码特征点结构形式 图1 编码特征点Fig.1 Coded targets

编码特征点图像的具体识别流程如下，首先拾取图像中封闭圆区域的边缘提取，由于中心圆区域可能会变形为椭圆，因此采用二次曲线拟合算法可计算编码特征点中心圆的中心坐标。在确定环状编码点中心圆的中心坐标之后，就可以实现单个环状编码点的提取，再根据环状编码点的编码规则将编码点代表的数字解码出来。此编码特征点解码流程如图2所示。

图2 编码特征点解码流程图Fig.2 Decode process of thecoded targets

3.2 立体目标单目视觉位姿测量算法

在透视投影模型下，利用被测目标空间共线误差作为最小化目标函数，三维位姿求解算法正交迭代算法，可直接得到正交旋转矩阵，进而得到目标坐标系与摄像机坐标系的相对位置关系，本算法可全局收敛，且具有较强的抗噪能力[6]。本文通过正交迭代算法可求解得到目标物体与单台摄像机之间的位姿关系，即三维六自由度参数，包含三个旋转参数和三个平移参数。

3.2.1 空间共线性误差

(2)

图3 目标空间共线性误差示意图Fig.3 Linear error probable of the object space

视线是指经过光心Oc和像点pi的射线，在视线投影矩阵Vi作用下，空间点Pi经在像平面的投影点为pi。空间点Pi应与其在对应像平面的投影点pi重合，可得目标空间共线方程，其代数形式如下

(3)

式中：R——旋转矩阵；t——平移矩阵。

3.2.2 正交迭代算法

摄像机位姿估计问题可转化为如下的目标空间共线误差最小化问题

(4)

由公式(4)可得，给定旋转矩阵R，t的最优解有如下形式的闭合解

(5)

(6)

(7)

公式(7)可用SVD法(奇异值分解法)求解，可保证旋转矩阵R的正交性。定义

(8)

(9)

令UTMV=D表示M的一个SVD分解，则公式(7)的解为Rk+1=VUT。SVD法可保证R的正交性，但是仍有det(Rk+1)=-1的可能性。故需要对所得解进行优化校正，即：Rk+1=Vdiag(1,1,det(VUT))UT，由公式(5)进而可得t的最佳估计值为：tk+1=t(Rk+1)，重复上述迭代步骤直至收敛。立体目标单目视觉位姿测量算法流程图如图4所示。

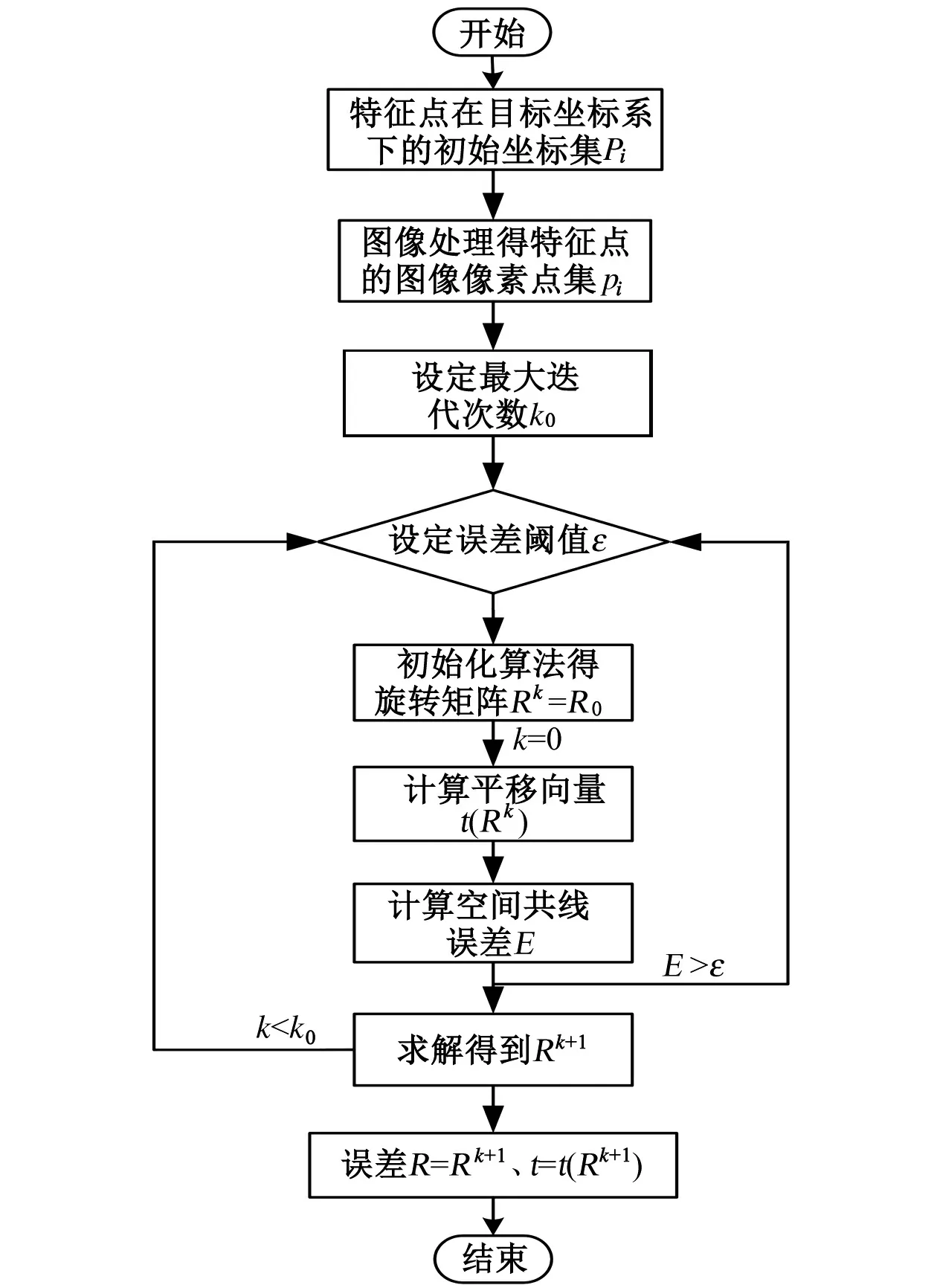
图4 测量系统流程图Fig.4 Process of the measurement

4 方法验证

4.1 位移测量误差测试

采用六面棱体作为模拟运动目标，棱体上不共面分布五个编码特征点，为了实现对单目视觉系统位移测量精度的测试，采用1.5m高精度具有位移测量和外触发信号输出功能的直线位移导轨作为位移标准装置，控制模拟目标以50mm为间隔沿直线导轨运动，测量得到单目视觉系统的位移测量值，将此测量值与位移标准装置进行比较，得到单目系统的位移测量误差值δ1，如图5所示。

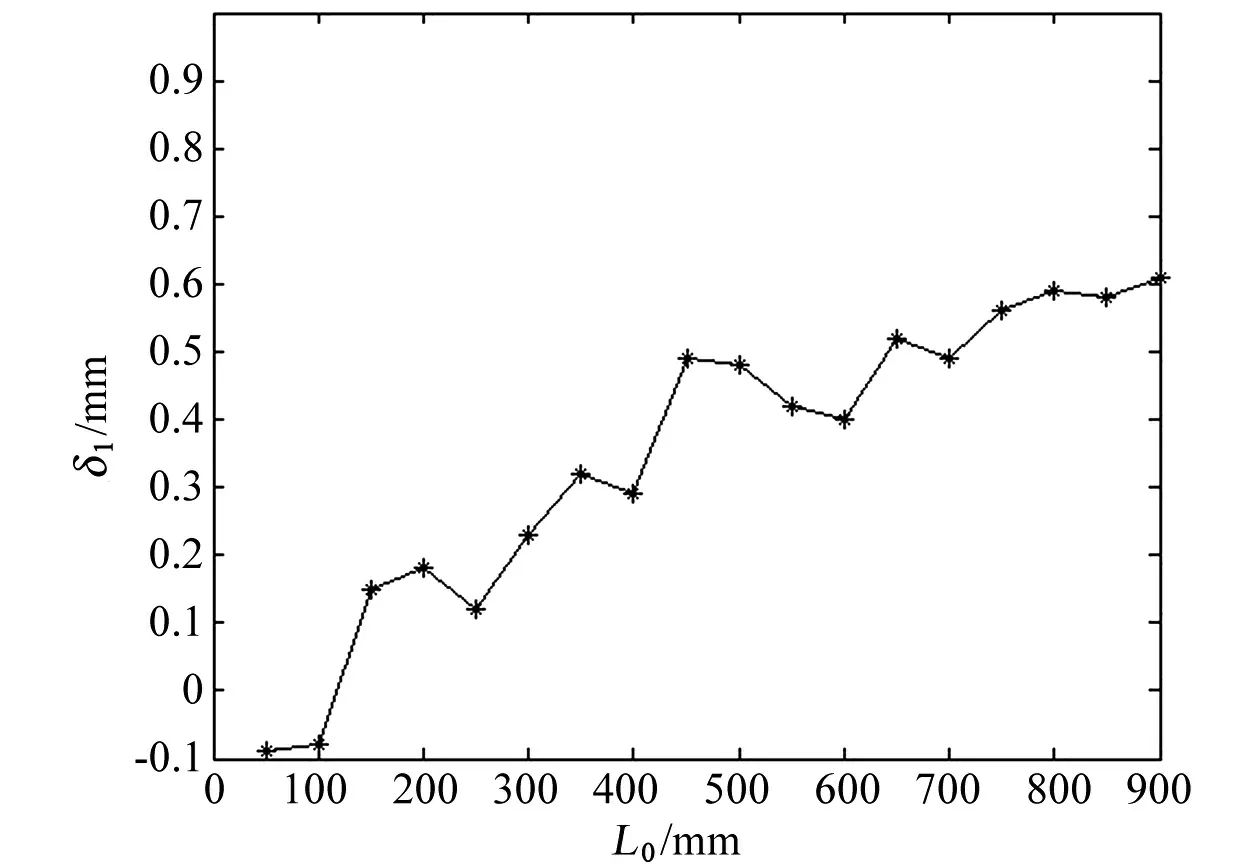
图5 目标位移测量误差图Fig.5 Measurement error of the target displacement

4.2 姿态测量误差测试

为了验证单目视觉系统姿态测量精度，采用具有定角外触发信号(码盘模拟信号)输出功能的三轴转台作为空间角度标准装置，以六面棱体作为模拟运动目标，使三轴转台以规定幅值和频率转动，以转台内部输出姿态角度值作为标准值θ0，采用大靶面高分辨率相机以一定的采样频率对模拟运动目标进行拍摄并采集，解算得到姿态角度测量值，进而得到单目系统的姿态测量误差值δ2，部分姿态测量误差值如图6所示。

图6 目标姿态角测量误差图Fig.6 Measurement error of the target attitude

本装置的主要技术指标为：在上述测量范围内，位移测量精度为2mm，姿态测量精度为0.2°。通过模拟运动目标位移和姿态角测量精度验证实验结果表明：位移测量误差小于2mm，单目系统的姿态测量误差小于0.2°。

5 测量不确定度评定

5.1 平移量不确定度评定

5.1.1 测量模型

由直线位移导轨给出标准位移测量值L0，与单目视觉解算位移值L1相比较，可得测量误差的测量模型

δ1=L1-L0

(10)

式中：δ1——平移量测量误差；L1——单目系统位移测量值；L0——直线位移导轨输出位移标准值。

对各影响量求偏导，得到灵敏度系数

(11)

合成不确定度公式为

(12)

5.1.2 不确定度来源

(1)测量重复性引入的不确定度分量u(L1)

用单目视觉系统对直线导轨给出的标准位移进行10次独立重复观测，观测值如表1所示，用贝塞尔公式计算单次测量值的实验标准偏差s(L)为

(13)

表1 10次独立重复观测值

以标准位移量150mm为例，以单次测量的标准偏差作为不确定度分量，即

u(L1)=s(L)=0.12mm

(14)

u(L1) =0.12mm

(2)直线位移导轨引入的不确定度u(L0)

由直线位移导轨校准证书可知，直线位移导轨测量误差为±0.02mm，则直线位移导轨测量误差引入的标准不确定度为：u(L0)=0.02mm。

(3)合成标准不确定度

校准系统引入的标准不确定度分量互不相关，按式(15)计算

(15)

uc(δ) =0.12mm

(4)扩展不确定度

取扩展因子k=2，则在此标准位移值下的扩展不确定度为

U=kuc(δ)

(16)

U=0.24mm

5.2 姿态角度测量不确定度评定

5.2.1 测量模型

以方位角为例，由三轴转台给出标准方位角度值θ0，与单目视觉解算方位角度值θ1相比较，可得方位角测量示值误差的测量模型

δ2=θ1-θ0

(17)

式中：δ2——方位角测量示值误差；θ1——单目系统输出方位角测量值；θ0——三轴转台输出标准方位角度值。

对各影响量求偏导，得到灵敏度系数

(18)

合成标准不确定度公式为

(19)

5.2.2 不确定度来源

(1)测量重复性引入的不确定度分量u(θ1)

在相同条件下，设置转台使方位轴从同一运动方向定位在5°位置，方位轴示值稳定后，手动触发单目视觉测量系统，测量当前方位轴角度，连续进行10次独立重复观测，观测值如表2所示，用贝塞尔公式计算单次测量值的实验标准偏差s(θ)为

(20)

表2 10次独立重复观测值

以其中任意一次作为测量结果，则由测量重复性导致的测量结果的标准不确定度为

u(θ1)=s(θ)

(21)

u(θ1)=0.01°

(2)三轴转台引入的不确定度

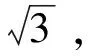
(22)

u(θ0)≈0.0006°

(3)合成标准不确定度

校准系统引入的标准不确定度分量互不相关，按式(22)计算，可得

(23)

uc(δ)=0.01°

(4)扩展不确定度

取扩展因子k=2，则在此标准角度下的扩展不确定度为

U=kuc(δ)

(24)

U=0.03°

6 结束语

本文采用环形编码特征点，研究基于一种不共面五点透视成像模型的正交迭代算法，求解得到相机坐标系与世界坐标系之间的旋转矩阵和平移矩阵，实现对目标物体的三维六自由度姿态测量，并对单目系统的平移、姿态测量精度进行测试，完成了对单目测量系统的测量不确定度评估。