基于恒定Hessian矩阵的三相最优潮流综合调压策略研究

汝石

摘   要：针对分布式发电（DG）接入配电网易引起综合电网潮流不稳定性问题，以支路电流作为未知变量建立了配电网三相有载分接开关（OLTC）的二次模型，旨在解决三相最优潮流（OPF）综合调压。以支路电流作为状态变量，OPF迭代的Hessian矩阵作为常量，利用高斯惩罚函数约束OPF问题中连续离散控制变量，结合二次惩罚函数约束Hessian矩阵的恒定性，构造了预測校正双内点法（PCPDIPM）求解配电网三相OPF。此外，将调压器整合到OPF模型中以形成综合调压策略。在改进的IEEE-13配电网三相不平衡测试系统上对该方法进行了测试和验证。

关键词：配电网;Hessian矩阵;最优潮流;综合调压

中图分类号：TM744                                           文献标识码：A

Study on Three-phase Optimal Power Flow of Distribution

Network Based on Constant Hessian Matrix

（State Grid Heilongjiang Electric Power Co.，Ltd.，Harbin，Heilongjiang 150090，China）

Abstract：Aiming at the problem of power flow instability in integrated power system caused by DG access to distribution network，a quadratic model of three-phase on-load tap changer（OLTC） in distribution network is established with branch current as an unknown variable，aiming at solving the integrated voltage regulation of three-phase optimal power flow（OPF）. Taking branch current as state variable and Hessian matrix of OPF iteration as constant，continuous discrete control variables in OPF problem are constrained by Gauss penalty function，and the invariance of Hessian matrix is constrained by quadratic penalty function. A predictive correction double interior point method（PCPDIPM） is constructed to solve three-phase OPF in distribution network. In addition，the voltage regulator is integrated into the OPF model to form a comprehensive voltage regulation strategy. The method is tested and validated in the improved three-phase unbalance test system of the IEEE-13 distribution network.

Key words：distribution network;Hessian matrix;optimal power flow;integrated voltage regulation

分布式发电DG（Distributed Generation）和各种离散可调装置的有源配电网的最优潮流OPF（Optimal Power Flow）问题是非凸且非线性的混合整数优化问题[1]。通过优化可调并联电容器[2]、可调分布式能源[3]、有载分接开关（OLTC）[4]的运行策略，OPF可将配电网损耗的运行成本降至最低。DG和储能装置给传统的OPF问题带来了新的挑战[5]。文献[6]利用割平面一致性算法（CPCA）研究了光伏发电对配电网OPF的分散式求解。文献[7]提出了基于OLTC的交直流混合配电网的分层控制策略，并结合二阶锥松弛法求解OPF。文献[8]优化主动配电网的运行，其中DG采用非耦合模型，得出近似结果。文献[9]提出了一种适用于DG的三相稳态布谷鸟算法。

旨在解决三相最优潮流（OPF）综合调压问题，以支路电流作为状态变量，OPF迭代的Hessian矩阵作为常量，利用高斯惩罚函数和二次惩罚函数分别约束OPF问题中连续离散控制变量和Hessian矩阵不变性，构造了预测校正双内点法（PCPDIPM）求解配电网三相OPF。通过电压调节器对配电网各相电压进行微调，并将其整合到OPF问题中，从而使各相电压进行微调，进一步优化配电网损耗。

1   三相配电网

1.1   三相OLTC的二次模型

在笛卡儿坐标系中，如果将OLTC的匝数比作为控制变量，则OPF模型是阶数大于二次的非线性优化问题。当采用内点法求解OPF问题时，每次迭代都会更新Hessian矩阵，从而导致较大的计算负担[10]。为了解决该问题，提出了一种新的三相OLTC模型，在OPF的迭代过程中，通过将支路电流作为状态变量，Hessian矩阵作为常量。

图1给出了Y型三角形（Yd）变压器配置中的OLTC，在分支 中添加了一个虚拟节点 。这将OLTC转换为理想变压器 （具有可调的匝数比 ），并与等效阻抗 （具有阻抗 ）串联。节点电压和支路电流也如图1所示。

对于理想的变压器，有

■ai = k（■am - ■bm）■bi = k（■bm - ■cm）■ci = k（■cm - ■am）       （1）

根据能量守恒，有

■ ai（■ ai）* + （■am - ■bm）（■ abm）* = 0■ bi（■ bi）* + （■bm - ■cm）（■ bcm）* = 0■ ci（■ ci）* + （■cm - ■am）（■ cam）* = 0       （2）

将公式（1）代入公式（2），可得：

k■ ai = - ■ abm*k■ bi = - ■ bcm*k■ ci = - ■ cam*       （3）

在三相系统中，以线路电压为基准电压。因此，对于Yd型变压器，每单位系统下的标准变换比为1 ： 3。考虑到等效阻抗分支mj，有

■ am - ■ aj = ■ a  mj（Ra + JXa）■ bm - ■ bj = ■ b  mj（Rb + JXb）■ cm - ■ cj = ■ c  mj（Rc + JXc）       （4）

1.2   三相DG的二次模型

包含DG的广义序列分量模型，如图2所示。

（a）正序                                        （b）负序

（c）零序

在图2中，上标“+”、“-”和“0”分别代表正序、负序和零序。Id + jIq表示从DG到配电网的电流，Ud + jUq表示耦合点的电压，R + jX表示阻抗，Urd + jUrq表示励磁电压。

DG控制系统由三部分组成：有功功率控制、无功功率控制和不平衡分量控制。其中，有功功率控制使得正序有功功率保持不变;无功控制使得注入电网的无功功率保持不变。不平衡分量控制使得DG励磁电压的正序分量，负序分量和零序分量均为零。从而建立等式约束，如下式所示：

Im[（U+d + jU+q）（I+d - jI +q）]=U+qI+d-U+dI+q=Qsp   （5）

Re[（U+d + jU+q）（I+d - jI +q）]=U+qI+d+U+dI+q=Psp   （6）

U 0rd=Re[（I 0d+ jI 0q）（I 0+ jX0）+U 0d+ jU 0q]=0U 0rq=Im[（I 0d+ jI 0q）（I 0+ jX0）+U 0d+ jU 0q]=0U-rd=Re[（I -d+ jI -q）（I -+ jX-）+U -d+ jU -q]=0U-rq=Im[（I -d+ jI -q）（I -+ jX-）+U -d+ jU -q]=0 （7）

其中，Re[]和Im[]分别对应于表达式的虚部和实部。Psp和Qsp分别对应于目标有功功率和无功功率的正序值。

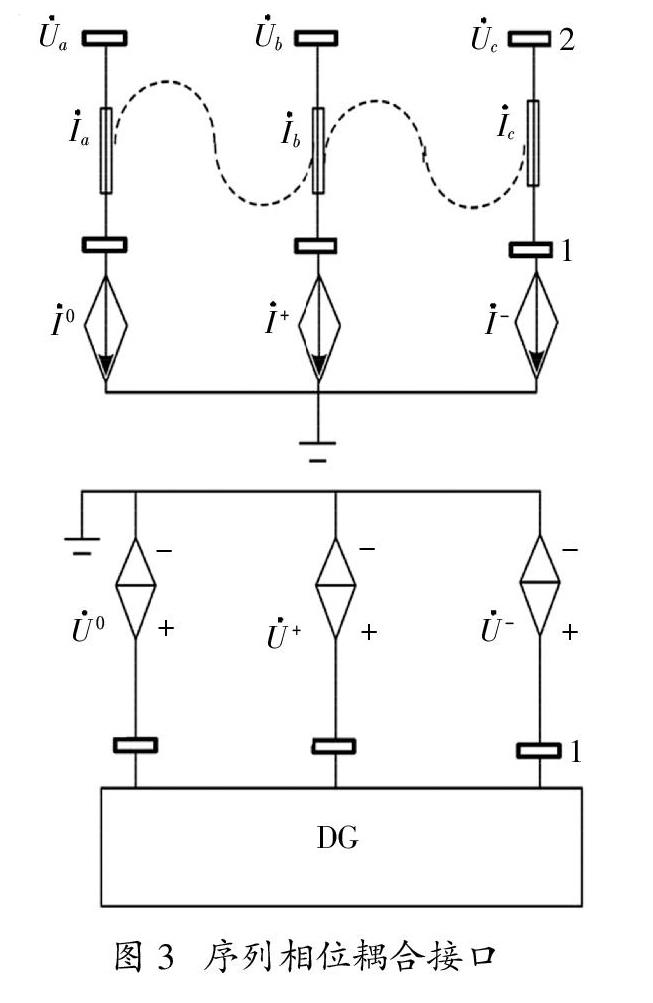
将三相耦合DG的配电网接口建模为电压控制电压源和电流控制电流源的相位序列耦合接口，如图3所示。

在DG二次模型中，注入电流和终端电压的序列值是未知变量。这些变量包括■ 0、■ +，■ -，■ 0，■ +和■ -。从相位值到序列值的转换为：

[■ 0   ■ +   ■ -]T = Tabc→0+- [■a    ■b   ■c ]T      （8）

[■ 0   ■ +   ■ -]T = Tabc→0+- [■a    ■b   ■c ]T      （9）

其中，Tabc→0+-为相序变换矩阵。·为对应复数。

约束条件（5）-（9）考虑了三相电源的耦合特性。与文献[11]中不考虑不平衡条件下的顺序控制的稳态模型不同。涉及DG的方程要么是线性的，要么是二次的，这保证了OPF中恒定Hessian矩阵。

常用的DG模型是三相非耦合模型[12]，描述如下：

P P + jQ P = （UPre + jUPim）（IPre - jIPim）    （10）

其中，P P和Q P分别对应DG在相P上的有功功率输出和无功功率輸出。UPre、UPim、IPre和IPim分别对应于DG在相P上的节点电压和注入电流的实部和虚部。DG的三相耦合模型为精确模型，三相非耦合模型为近似模型。因此，三相耦合模型的OPF结果比近似三相非耦合模型的OPF结果更准确。

上述公式构建了三相OPF模型的DG约束条件。由于这些公式的最高阶是二次的，因此，Hessian矩阵在整个迭代过程中是常数。

1.3   三相调压器模型

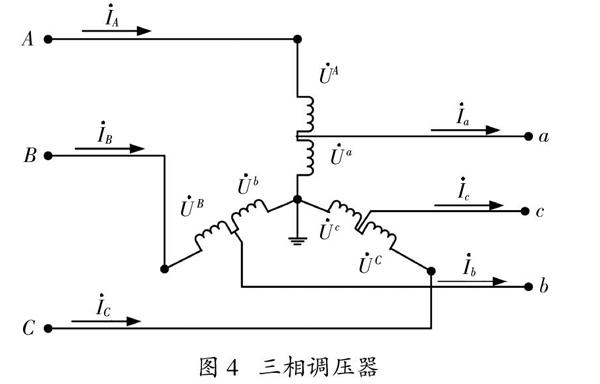
电压调压器与配电网相连，并实现了对节点电压的微调作用。三相Y型连接调压器由三个单相调压器组成，且每个单相调压器都有一个分接开关来改变分接位置。三相调压器的结构如图4所示。

并适用下列限制：

■A = ka■a■B = kb■b■C = kc■c       （11）

ka ■ A = ■ akb ■ B = ■ bkc ■ C = ■ c       （12）

ka  = 1 ± 0.006 25 × Tapakb  = 1 ± 0.006 25 × Tapbkc  = 1 ± 0.006 25 × Tapc       （13）

其中，加号（“+”）对应于“升序”，减号（“？”）对应于“降序”。“Tap”表示调压器分接头的位置（例如，在±5%范围内的32级调节）。该接头由线路电压降补偿装置来控制负载中心的电压。线路电压降补偿器通过电压互感器（匝数比NPT ：1）和电流互感器（匝数比CTP ：CTS）与配电线路耦合，如图5所示。

补偿器的阻抗表示从调节器到负载中心的等效阻抗：

R′ + jX′ = （R + jX）■      （14）

负载中心的电压为：

■ x     load = ■ - ■     （15）

如果負载中心的电压水平为240 V，带宽为4 V，则每当调压器的分接头移动到下一个位置时，电压将变化1.5 V。升压和降压接头的变化分别为：

Tapx = ■     （16）

Tapx = ■     （17）

2   OPF模型和算法

2.1   OPF模型

以节点电压和支路电流为状态变量，建立了配电网三相OPF模型。OPF模型的目标函数是配电网的最小损耗，如下方程所示：

min f（x）=Ploss=■■■br，P ■br，P Δt    （18）

其中，为配电网中支路的数量。 、 分别对应于第 个支路相P上的支路电压和支路电流。其中，支路电压是支路两端的节点电压之差。

这些方程包括KCL和KVL约束，如公式（19）所示，变压器支路约束，如公式（1）、（3）和（4））所示，DG支路约束，如公式（5）-（9）所示、调压器支路约束，如公式（11）和（12）所示。

Ubr，P，re = AUn，P，reUbr，P，im = AUn，P，im0 = AT Ibr，P，re0 = AT Ibr，P，im      （19）

其中，Ubr，P，re、Ubr，P，im、Ibr，P，re和Ibr，P，im分别对应于第br个支路相P上支路电压和支路电流的实部和虚部。Un，P，re和Un，P，im分别对应第n个节点相P上节点电压的实部和虚部。A是节点支路关联矩阵。

状态变量约束包括发电机有功功率和无功功率Pij约束、节点电压幅值约束和线路传输功率 约束，如公式（20）所示。控制变量约束包括OLTC匝数比KT、调压器分接头位置KV、无功电容补偿容量 QC约束，如公式（21）所示。

P -      Gi，P ≤ PGi，P ≤ P +      Gi，PQ -      Gi，P ≤ PGi，P ≤ Q +      Gi，PU -   i，P ≤ U 2         i，P，re + U 2         i，P，im≤ （U +   i，P）2       （20）

K -    T，i ≤ KT，i ≤ K +     T，iK -    V，i ≤ KV，i ≤ K +     V，iQ -    C，i ≤ QC，i ≤ Q +     C，i       （21）

因此，OPF模型中的方程可以是线性的，也可以是二次的，当采用内点法求解时，保证了一个恒定的Hessian矩阵。本文利用PCPDIPM[13]求解优化模型，可实现具有收敛速度快、效率高等优点。

2.2   连续变量离散化过程

有源配电网的OPF问题涉及离散控制变量（如OLTC匝数比、电容补偿容量等）。目标函数包含一个惩罚函数来处理离散变量。这给目标函数引入了虚拟损失，从而减少了四舍五入带来的误差。目前，二次惩罚函数[14]和高斯惩罚函数[15]是两种常用的惩罚函数，其公式分别为：

准（x） = ■■v（xi - bi）2    （22）

准（x） = vG（x） = vexp-■■    （23）

其中，v为惩罚因子。当从向量x=（x1，x2，…，xn）T到中心b = （b1，b2，…，bn）T的距离降至0时，函数值将为零。惩罚函数代入公式（18）可得：

min Ploss = ■■■br，P ■br，P Δt + ？准    （24）

当惩罚因子足够大时，将离散控制变量优化为对应的离散值，使惩罚函数值变为零且目标函数达到最小值。与二次惩罚函数相比，随着向量 与 之间距离的减小，高斯惩罚函数比二次惩罚函数下降得更快，并且高斯惩罚函数对离散变量的变化更为敏感。然而，高斯惩罚函数是一个非二次函数，这使得Hessian矩阵在迭代过程中不断发生变化，进而降低计算效率。

3   实验分析

设计了配电网三相最优潮流综合调压策略的OPF模型，利用MATLAB上对模型进行了实验分析。对改进后的IEEE-13测试系统进行OPF分析，如图6所示。

图6中省略了互阻抗和互导纳。控制变量为发电机无功功率、DG输出、OLTC匝数比、调压器分接头位置、电容器匝数比，其中OLTC匝数比与电容器匝数比为离散控制变量。匝数比范围设定为1.8-2.2且分为8个接头，其步长为0.025。电容器的最大无功功率为0.04 pu。步长为0.02。所有节点电压的范围为1.8 - 2.2 p.u。调压器分接头为32级可调节接头，调节范围±5%，负荷中心电压电平为240 v，带宽为4 v。

3.1   三相OLTC二次模型分析

为了验证提出的三相OLTC在有源配电网OPF问题中的合理性，本文采用基于PCPDIPM嵌入二次惩罚函数（PCPDIPM-QPF）的优化潮流计算方法，将所提出的三相OLTC二次模型与文献[16]中的三相OLTC非二次模型进行了比较，结果如表1所示。

由表1可见，两种方法使用不同模型的结果（配电网损耗）相同，但是二次模型计算速度更快。这是由于OLTC非二次模型的Hessian矩阵在OPF计算过程中不是常数，每次迭代都会更新，使得计算速度非常慢。而OLTC二次模型在整个迭代过程中确保了Hessian矩阵为常量，抑制了迭代过程中Hessian矩阵的计算量，从而大大减少了计算时间。此外，两种模型的计算时间相对都较长。这是由于Hessian矩阵是用Matlab的自动微分函数生成，虽然方便但效率不高。然而，这并不影响本文的结论。

实验总共进行了34次迭代。Hessian矩阵在Intel core i3-3240M CPU 3.40 GHz、4GB内存的计算机上计算一次需要5.56s。因此，对非二次模型计算时间的保守估计为计算Hessian矩阵时间的34倍，即189.04s。这也验证了表1计算时间的合理性。

3.2   连续变量离散化过程分析

为了验证OPF计算中二次惩罚函数和高斯惩罚函数的收敛性，设计了PCPDIPM-QPF和PCPDIPM嵌入高斯惩罚函数（PCPDIPM-GPF）。用这两种算法计算了改进后的IEEE-13三相系统的OPF。通过对优化结果（网络损耗）、迭代次数和计算时间（精度为e-10）的比较，证明了每种方法的优缺点。OPF计算结果，如表2所示。

由表2可见，PCPDIPM-GPF的优化效果优于PCPDIPM-QPF（配电网损耗降低2.4%）。然而，PCPDIPM-GPF的迭代次数略高于PCPDIPM-QPF，且PCPDIPM-GPF耗时较长。这是由于高斯惩罚函数是高阶函数，而Hessian矩阵在整个迭代过程中是非常量矩阵。因此，Hessian矩阵随着迭代次数的增加也随之更新，从而增加了计算时间。PCPDIPM-QPF与PCPDIPM-GPF的比较结果，如图7所示。

可以看出，随着迭代次数的增加，对偶间隙减小，当两个罚函数收敛效果达到期望值时，PCPDIPM-QPF的速度比PCPDIPM-GPF快4倍。

3.3   綜合调压策略分析

采用改进的IEEE-13三相调压系统实现了OPF的综合调压策略。综合调压的最优潮流结果如表3所示。

由表3可知，电压调节器对有源配电网各相电压微调的作用，并在OPF计算中可以进一步降低配电网损耗。与不含调压器的配电网相比，有调压器的配电网损耗降低了0.22%。综合调压前后各节点三相电压分布分别如图8至图10所示。

由此可见，在OPF计算中，电压调节器可以调节各相节点电压，进一步降低配电网损耗。

4   结   论

针对配电网三相最优潮流控制问题，提出了三相OLTC的二次模型并整合到OPF模型中，使得Hessian矩阵在整个迭代过程中变为常量，采用二次惩罚函数与高斯惩罚函数相结合的内点法求解有源配电网三相OPF问题，进而提高了计算效率。结合调压器构建了综合调压策略，利用改进的IEEE-13配电网验证了所提模型的有效性。

参考文献

[1]    王龙宇，王丙东，蔡蕾，等. 考虑分布式电源影响的电网运行安全风险评估方法概述[J]. 电气工程学报，2016，11（12）：30-36.

[2]    王俊星.一组35 kV并联电容器组干式放电线圈绝缘缺陷分析[J]. 电力电容器与无功补偿，2018，39（06）：80-83+90.

[3]    张佳琦，王林川. 主动配电网电压协调控制策略[J]. 东北电力大学学报，2017，37（04）：14-19.

[4]    李超，赵志刚，王亮，等. 含分布式发电的配电网无功电压优化的研究[J]. 沈阳工程学院学报（自然科学版），2019，15（01）：78-81.

[5]    张小和. 含分布式发电的配电网规划方法研究[J]. 机电工程技术，2016，45（02）：85-89.

[6]    戴月，刘明波，王志军，等. 高光伏渗透配电网分散式最优潮流的割平面一致性算法[J]. 电力系统自动化，2018，42（15）：2-10+38.

[7]    孟明，朱国林，魏怡. 基于最优潮流的交直流配电网分层控制策略[J]. 电力建设，2018，39（08）：94-101.

[8]    韩禹歆，陈来军，王召健，等. 基于自适应步长ADMM的直流配电网分布式最优潮流[J]. 电工技术学报，2017，32（11）：26-37.

[9]    张宸瑞. 布谷鸟算法的含分布式电源配电网最优潮流优化[J]. 现代电子技术，2017，40（15）：159-162.

[10]  郭屾，王鹏，栾文鹏，等. 基于PMU的配电网潮流雅可比矩阵鲁棒估计与拓扑辨识[J]. 电力系统及其自动化学报，2018，30（10）：68-76.

[11]  陈欣，陈乾宏，何广明. 强耦合条件下非接触滑环工作特性分析与控制[J]. 电力系统自动化，2018，42（23）：105-121.

[12]  陈晓，陈恒林，陈国柱. 基于耦合电感的三相四线制并联有源电力滤波器[J]. 浙江大学学报（工学版），2015，49（08）：1529-1536.

[13]  NIE Y，DU Z，WANG Z，et al. PCPDIPM based optimal reactive power flow model with discrete variables[J]. International Journal of Electrical Power & Energy Systems，2015，69：116-122.

[14]  王波，濮定國. 新的无罚函数无滤子的序列二次规划方法[J].同济大学学报（自然科学版），2016，44（05）：807-811.

[15]  邓长虹，马庆，肖永，等. 基于自学习迁移粒子群算法及高斯罚函数的无功优化方法[J]. 电网技术，2014，38（12）：3341-3346.

[16]  赵婷婷，赵凤展，巨云涛，等. 基于定常海森矩阵的配电网三相最优潮流模型[J]. 电力系统自动化，2018，42（15）：11-17+284-285.