基于门控递归神经网络的电网日峰值负荷预测
吴福疆 范晟 王振达 王烁

摘 要:日峰值负荷作为非线性、非平稳且波动的时间序列,难以准确预测。提出了一种结合动态时间规整(DTW)的门控递归神经网络(GRNN)用于准确预测日峰值负荷。利用DTW距离用于匹配最相似的负荷曲线,可以捕捉负荷变化趋势。采用热编码方案对离散变量进行编码,扩展其特征从而表征对负荷曲线的影响。提出了一种基于DTW的门控递归单元(DTW-GRU)算法用于日峰值负荷预测,并在欧洲智能技术网络(EUNITE)数据集上进行了测试。仿真结果表明,与其他算法相比,该算法的MAPE仅为1.01%。
关键词:峰值负荷预测;动态时间规整;热编码;门控递归单元
中图分类号:TP181;TM715 文献标识码:A
Daily Peak Load Forecasting Based on Gating Recurrent Neural Network
WU Fu-jiang?覮,FAN Sheng,WANG Zhen-da,WANG Shuo
(Shantou Power Supply Bureau,Guangdong Power Grid Co.,Ltd.,Shantou,Guangdong 515000,China)
Abstract:As a non-linear,non-stationary and fluctuating time series,daily peak load is difficult to predict accurately. A gated recurrent neural network (GRNN) combined with dynamic time warping (DTW) is proposed to predict daily peak load accurately. DTW distance is used to match the most similar load curve,which can capture the trend of load change. The thermal coding scheme is used to encode the discrete variables and extend their characteristics to represent the influence on the load curve. A DTW-GRU algorithm based on DTW is proposed for daily peak load forecasting,and it is tested on the European Intelligent Technology Network (EUNITE) dataset. Simulation results show that the MAPE of this algorithm is only 1.01% compared with other algorithms.
Key words:peak load forecasting;dynamic time regulation;thermal coding;gated recursive unit
日峰值负荷预测是电力系统运行规划决策的重要工具。负荷预测可分为短期负荷预测、中期负荷预测和长期负荷预测[1]。日峰值负荷预测作为一种中期负荷预测,可作为评估电力系统备用容量、日负荷率以及制定峰谷电价的重要依据[2]。大多数预测模型都是基于相似性原理和各种优化算法且可以分为两类[3]:经典的预测算法和智能预测算法。
对于经典的预测算法,其主要优点是计算速度快、鲁棒性强。文献[4]和文献[5]分别利用频域分量法和小波分析法从频域角度研究负荷,但没有考虑社会因素、气象因素等其他因素对峰值负荷的影响。衡量两个时间序列之间相似性的常用的方法有欧氏(Euc)距离、曼哈顿(Manh)距离、余弦角(Cos)和相关系数(Cor)距离[6]。然而,这些方法只能描述两个序列整体的相似度,并且容易掩盖很多局部信息。
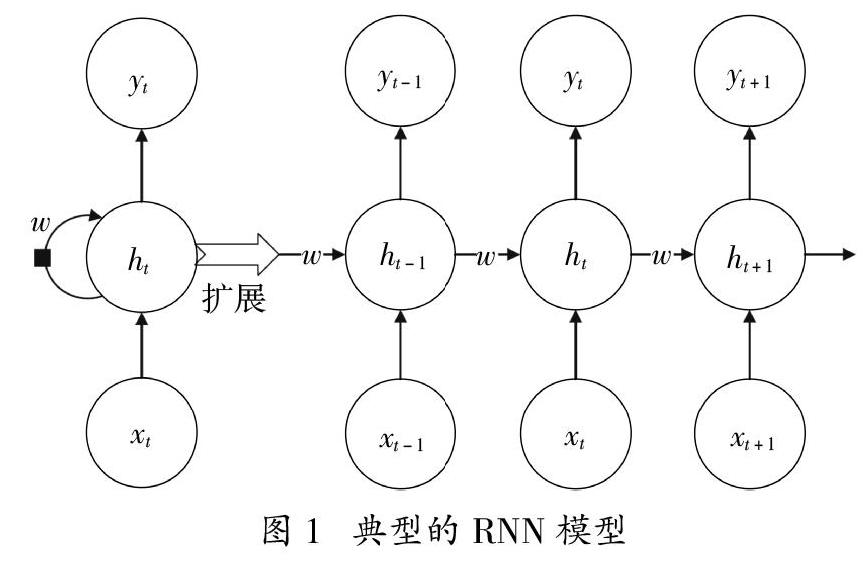
对于智能预测算法,其优势在于筛选和处理影响负荷曲线的主要因素。基于人工神经网络(ANN)和支持向量机(SVM)可衍生出主成分分析人工神经网络(PCA-ANN)[7]、最小二乘支持向量机(LS-SVM)[8]、经验模式分解支持向量機(EMD-SVM)[9]和混沌支持向量机(Chaos-SVM)[10]来提高日峰值负荷预测的精度。然而,这些传统的神经网络方法没有考虑负荷曲线的时间序列特性,容易陷入局部最优和过拟合。与传统的神经网络相比,递归神经网络(RNN)引入了方向环来处理输入之间的上下文关联。文献[11]基于长期短期记忆(LSTM)的深度学习预测框架来预测负荷趋势。与LSTM相比,门控递归单元(GRU)参数少,并且更易于收敛[12]。
为了克服传统预测算法的不足,提出了一种基于门控递归神经网络(GRNN)和动态时间规整(DTW)的预测算法。利用自相关系数确定日峰值负荷曲线段的长度,采用DTW方法对最相似的负荷曲线进行匹配。与上述传统的测量距离方法不同,DTW距离不仅可以捕捉负荷曲线的变化趋势,而且可以捕捉负荷曲线的局部信息。在日历信息上应用热点编码方案以扩展预测功能,从而进一步表征其对负荷预测的影响。提出了一种基于DTW的门控递归单元(DTW-GRU)算法用于日峰值负荷预测。
1 DTW-GRU算法
2 負荷预测的实现步骤
设计开发了一种新的DTW-GRU算法用于日峰值负荷预测。所提出的DTW-GRU算法流程图,如图4所示。该算法分为四个阶段:(1)选择N个日峰值负荷;(2)利用DTW距离匹配负荷曲线;(3)编码相关影响因素;(4)利用GRNN预测日峰值负荷。
2.1 选择N个日峰值负荷
日峰值负荷曲线段的长度由自相关系数决定。自相关系数用来描述不同时期数据本身的关联程度,即衡量历史数据对当前的影响。对于时间序列{xt},xt和xt - 1之间的相关系数称为间隔l为xt 的自相关系数。自相关系数表示为:
ρl = ■ (8)
其中,Cov(xt,xt-1)为自方差,Var(xt)和Var(xt-1)为方差。自相关系数越大,历史数据对当前的影响越大。对于自相关系数序列{ ρl },其最大值为ρN。则最优时间间隔N是ρN的下标值。
2.2 使用DTW距离匹配负荷曲线
为了得到最相似的日峰值负荷,考虑到电力系统负荷具有一定的规律性和周期性,采用最小DTW距离的日峰值负荷相似匹配方法。首先,将原始数据集分为历史数据集和预测数据集。然后将原始数据集的每个区段与历史数据集进行匹配,得到最相似的区段。根据经验法则,如果两个区段相似,则对应的下一个区段也相似[16],则得到最相似的日峰值负荷。最相似日峰值负荷的曲线匹配,如图5所示。
历史数据集中有n个区段,原始数据集中有 个区段(0 < n < m)。每个区段为1 × l的向量,其中,l为每个区段的长度,其值在阶段1中获得。对于原始数据集中的任何区段元素(第1区段除外),第i + 1个区段中的第p个元素定义为预测目标(i,p > 0)。采用DTW匹配方法找出历史数据集中第i个区段中最相似的区段。假设第i个区段的最小DTW距离是历史数据集中的第j个区段(i≠j,j > 0),则历史数据集中第j + 1个区段的第p个元素是最相似的日峰值负荷。
2.3 编码相关影响因素
为了对相关影响因子进行编码,假定影响日峰值负荷的因素分为两个方面:一是气象因素,如温度和降水;二是社会因素,如日历信息。
对于气象因素等连续变量进行归一化处理,然后采用自然编码方法对其进行编码。归一化公式为:
xc = ■ (9)
其中,xc为归一化的结果,xo为原始输入数据,xmax和xmin分别为原始数据的最大值和最小值。
对于离散变量,采用了热编码方案[17]。热编码使用N位状态寄存器来编码N个状态。每个状态都有自己独立的寄存器位,并且在任何时候,只有一个是有效的。即对于任何状态,只有一个位是1,其他位是0。不同的日历信息编码结果,如图6所示。
从图6可以看出,该编码方案为每天定义两个属性:第一个属性为它是否是假日。每天定义三个条件,(1)首先是假日;(2)节前和节后(过渡日);(3)工作日。工作日的自然编码结果为0,其热编码结果为[1 0 0]。过渡日的自然编码结果为0.5,其热编码结果为[0 1 0]。假日的自然编码结果为1,其热编码结果是[0 0 1]。第二个属性用来标记它属于一周中的哪一天。从周日到周六,它们的自然编码为0至6,对于其热编码,分别设计了两种编码方案:全热编码方案和独热编码方案。对于全热编码方案,使用 7位编码方案来区分一周中的7天。对于独热编码方案,只使用2位编码方案来区分工作日和周末,这样既节省了计算资源,又能区分其本质特征。
2.4 利用GRNN预测日峰值负荷
采用GRNN对日峰值负荷进行预测包括4个步骤:(1)数据预处理;(2)模型构建;(3)模型训练和测试;(4)结果评估。
(1)数据预处理:为了利用深度学习模型进行负荷预测,将构建适当格式的训练集和测试集。对于训练集和测试集的每个元素都有两个部分,即GRNN的输入矩阵X和输出矩阵Y。矩阵X由[ A B C ]三个部分组成,其中A,B和C是从上述三个阶段获得的子矩阵。子矩阵A是阶段1的输出,即目标预测日前N天的日峰值负荷。子矩阵B是阶段2的输出,这是通过DTW匹配方法得到的最相似的日峰值负荷。子矩阵C是阶段3的输出,它是相关影响因素(包括气象数据和日历数据)的编码结果。矩阵Y是需要预测的日峰值负荷。
(2)模型构建:为了选择适用于负荷预测的深度学习模型。由于GRU独特的复位门和更新门结构,使得输入数据的长度可变。对于深度学习模型,文献[18]的研究表明,网络的性能对层数和层大小的任何组合都相对不敏感。根据文献[19]中的发现,多层比单层计算结果更好,隐藏节点的数量应该足够大。模型结构包含三层GRNN和一层FNN。
(3)模型训练和测试:模型建立后,利用预处理训练集对模型进行训练。然后使用测试集对模型进行测试。
(4)结果评价:对预测日峰值负荷结果进行评估。
3 DTW-GRU算法的实现
3.1 数据源
采用欧洲智能技术网络(EUNITE)竞赛负荷预测样本数据,数据资料主要包含:(1)1997年1月至1999年1月,每30分钟一次的电力负荷数据;(2)1997年1月至1999年1月的日平均温度;(3)1997年至1999年的假日。其中,1997年至1998年的日峰值负荷,如图7所示,1997年至1998年的日平均温度,如图8所示。
以761天的日峰值负荷为原始数据,共占据109周。由于109周中共有763天,超过761天,因此使用0来填补空白。前104周作为历史数据集,后5周作为预测数据集。
3.2 数据分析
(1)初步分析:对于电力负荷这类随机过程,利用自相关系数来确定其合适的模型阶数。以不同的间隔天数计算自相关系数。结果如图9所示。
从图9可以看出,自相关系数的最大值为7天,这与人类一周7天的社会活动周期相一致。因此,7天的倍数适用于负载区段。
(2)详细分析:日历信息从图7可以看出,周末(周六和周日)的负荷通常低于工作日(周一到周五)。此外,结合地区的假日情况,假日对负荷也有影响。假日的负荷通常低于非假日。因此,有必要利用包括周末和假日在内的日历信息来预测日峰值负荷。
在温度信息数据集中,样本数据提供的唯一气象信息是日平均温度。通过图7和图8相比,较高的温度对应较低的负荷,负荷与日平均温度呈负相关,计算值为-0.868。因此,日平均温度是建立预测模型的重要指标。
3.3 硬件和软件平台
设计在高性能的曙光I620-G15服务器上实现,该服务器配备了Ubuntu 14.04操作系统和2台NVIDIA GTX 1080设备。深度学习过程使用Keras神经网络库和Theano后端来构建,利用Theano平台和统一计算设备架构(CUDA)[20]实现了训练RNN的GPU加速。使用数据科学中常用的Python编程语言。
3.4 实验设置
为了实现DTW-GRU算法的最佳性能,结合文献[12]设计的GRU训练配置参数,将DTW-GRU算法的所有实验参数设置如下:
输入向量∈{10,13,17,18,20,25}
输出向量∈{1}
隐藏神经元数∈{200}
训练批量大小∈{10,20,30,50}
训练方法∈{自适应矩估计优化算法}
学习率∈{0.1,0.05,0.02,0.01}
训练停止策略∈{早停法}
损失函数∈{RMSE}
4 实验分析
将DTW距离与Euc距离、Manh距离、Cos距离和Cor距离4种常用距离类型来衡量负荷曲线的相似性,将原始数据集的108周(最后一周除外)与历史数据集的103周(最后一周除外)进行匹配。此外,在测试数据集的输入中使用了最相似的日峰值负荷。
利用Kupiec测试和典型误差指标对负载预测结果与其他算法进行比较。首先,通过Kupiec测试来验证模型性能,Kupiec测试的基本思路是计算测试期间与故障率相对应的统计值,以确定模型是否有效。预测误差定义如下:
fe = ■ × 100% (10)
其中,■t为预测值,yt为实际值。
失效天数是预测误差超过给定误差的天数。假设周期为P天,其中Q天失效,计算出失效率为:
f = ■ (11)
同樣,假设时间独立,并且失效天数Q遵循二项分布B(P,f)。对于显着性水平α,似然比检验(LR)服从自由度为1的卡方分布:
LR = 2ln[(1-f)P - Q f Q ] - 2ln[(1-α)P - QαQ ] (12)
在α = 5%的显着性水平下,当LR > 5.02时,则拒绝该模型。其次,为了评估所提出的方法在进行负荷预测方面的性能,使用了三个常使用的指标:平均绝对百分比误差(MAPE)、最大误差(ME)和均方根误差(RMSE),它们的定义如下:
MAPE = ■■■ × 100% (13)
ME = max■t - yt,t = 1,2,…,N (14)
RMSE = ■ (15)
其中,N为预测集大小。从三个方面比较日峰值负荷预测的结果:不同的距离、不同的编码方案和不同算法结构。
4.1 不同距离类型比较
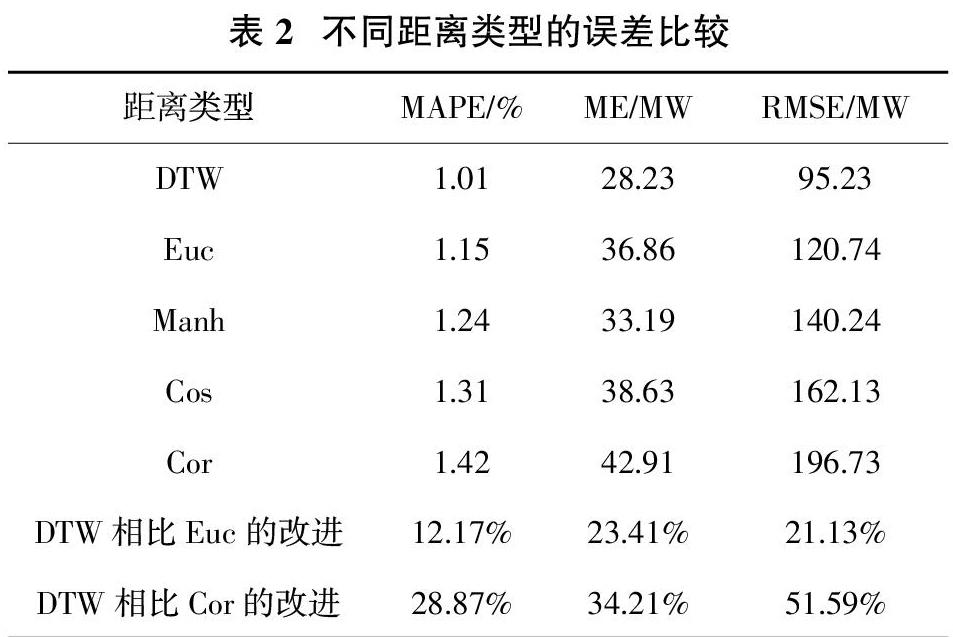
对不同距离类型进行比较的LR值,如表1所示。
符号“√”表示此距离类型在a = 5%显著性水平下通过Kupiec检验。随着误差率的增加,越来越多的距离类型通过了Kupiec检验。当预测误差率阈值为1.75%时,DTW距离和Euc距离均通过Kupiec检验。当预测误差率阈值为2.50%时,Manh距离和Cos距离均通过Kupiec检验。当预测误差率阈值为3.00%时,Cor距离通过Kupiec检验。总之,DTW距离和Euc距离优于Manh距离、Cos距离和Cor距离。
从表2可以看出,使用各种距离匹配方法的结果是:DTW>Euc>Manh>Cos>Cor,DTW距离与性能次优的Euc距离相比,MAPE、ME和RMSE的预测精度分别提高了12.17%、23.41%和21.13%。与性能最差的预测方法Cor距离相比,MAPE、ME和RMSE的预测精度分别提高了28.87%、34.21%和51.59%。
日峰值负荷作为非平稳的时间序列,获得最相似曲线的常用距离计算方法主要集中在任意两点之间的最短距离。这种方法忽略了曲线变化的趋势,难以解决负荷预测的非平稳性问题。然而,DTW距离可以捕获负荷曲线的变化趋势,从而在一定程度上获得负荷曲线的非平稳信息。此外,GRU独特的复位门和更新门结构可以存储和学习DTW距离匹配得到的负荷变化趋势。
4.2 不同编码方案比较
符号“√”表示此编码方案在α = 5%显著性水平下通过了Kupiec检验。当预测误差率阈值为1.75%时,只有独热编码方案通过了Kupiec检验。当预测误差率阈值为2.00%时,自然编码方案通过了Kupiec检验。当预测误差率阈值为2.50%时,全热编码方案通过了Kupiec检验。综上所述,使用各种编码方案的结果是:独热编码>自然编码>全热编码。
从表4可以看出,与自然编码方案相比,使用独热编码方案和全热编码方案,均可以有效地提高负荷预测的准确性。与自然编码相比,独热编码方案的MAPE、ME和RMSE的预测精度分别提高了15.83%、25.51%和26.03%。与全热编码方案相比,独热编码方案对MAPE、ME和RMSE的预测精度分别提高了6.48%、12.00%和16.78%。这是由于使用独热编码方案可以起到扩展离散变量特征的作用,扩展后的特征能够有效地刻画负荷变化的类型,有利于解决负荷预测中的波动性问题。相对于独热编码方案,采用全热编码方案的预测结果较差。这是由于全热编码方案扩展了太多的特征,而有用的特征占比下降了。因此,独热编码方案可以得到最好的预测效果。
4.3 不同算法比较
为了进一步证明所提出的DTW-GRU算法的有效性,与其他4种负荷预测算法在EUNITE测试集上的结果进行了比较,如表5所示。
从表5可见,传统GRU算法优于PCA-ANN算法[7]、LS-SVM算法[8]和Chaos-SVM算法[10],得到的MAPE为1.49%。由于GRU的特殊结构,并且EMD够处理非线性时间序列,因此,EMD-GRU算法[9]优于传统GRU算法。最终结果表明,提出的DTW-GRU算法优于其他4种算法,且MAPE仅为1.01%。将独热编码方案与DTW距离匹配方法相结合,对改进传统的GRNN非常有效。
5 结 论
将DTW距离与GRNN相结合对日峰值负荷进行预测。DTW距离可以有效地捕捉负荷变化趋势,独热编码方案可以扩展离散变量的特征,将它们作为RNN的额外输入可以使预测更加准确。在EUNITE数据集上的仿真结果表明,DTW-GRU算法能够显著提高日峰值负荷的预测精度,并且优与其他预测算法。
参考文献
[1] 邓永生,焦丰顺,张瑞锋,等. 配电网规划中电力负荷预测方法研究综述[J]. 电器与能效管理技术,2019,14(01):1-7.
[2] 朱俊丞,杨之乐,郭媛君,等. 深度学习在电力负荷预测中的应用综述[J]. 郑州大学学报(工学版),2019,40(05):13-22.
[3] 辛苗苗,张延迟,解大. 基于电力大数据的用户用电行为分析研究综述[J]. 电气自动化,2019,41(01):1-4.
[4] 谢毓广,张金金,陈凡,等. 基于频域分解的短期负荷预测[J]. 电工技术,2019(21):42-44.
[5] 黃青平,邹晓明,刘楚群,等. 基于小波分解与随机森林的短期负荷预测[J]. 电力信息与通信技术,2019,17(09):24-29.
[6] 李正欣,张凤鸣,张晓丰,等. 多元时间序列相似性搜索研究综述[J]. 控制与决策,2017,32(04):577-583.
[7] YU Z,NIU Z,TANG W,et al. Deep learning for daily peak load forecasting-a novel gated recurrent neural network combining dynamic time warping[J]. IEEE Access,2019,7(1):184-194.
[8] XIA C,ZHANG M,CAO J. A hybrid application of soft computing methods with wavelet SVM and neural network to electric power load forecasting[J]. Journal of Electrical Systems and Information Technology,2018,5(3):681-696.
[9] JUN W,LINGYU T,YUYAN L,et al. A weighted EMD-based prediction model based on TOPSIS and feed forward neural network for noised time series[J]. Knowledge-Based Systems,2017,132(12):167-178.
[10] YU Z,NIU Z,TANG W,et al. Deep learning for daily peak load forecasting-a novel gated recurrent neural network combining dynamic time warping[J]. IEEE Access,2019,7(01):184-194.
[11] 王晓霞,徐晓钟,张彤,等. 基于集成深度学习算法的燃气负荷预测方法[J]. 计算机系统应用,2019,28(12):47-54.
[12] 魏海文,郭业才. 门控递归单元神经网络坐标变换盲均衡算法[J]. 微电子学与计算机,2019,36(09):89-93.
[13] 张振球. 一种改进时间效率的动态规划算法的设计与实现[J]. 电子制作,2019,(24):76-77.
[14] 刘永利,武帅,杨立身. 基于快速动态时间规划的模糊聚类算法[J]. 河南理工大学学报(自然科学版),2017,36(06):111-116.
[15] 孙晓丽,郭艳,李宁,等. 基于改进RNN的多变量时间序列缺失数据填充算法[J]. 信息技术与网络安全,2019,38(11):47-53.
[16] 周驰,李智,徐灿. 基于DTW算法的空间目标结构识别研究[J]. 计算机仿真,2019,36(09):98-102.
[17] 梁杰,陈嘉豪,张雪芹,等. 基于独热编码和卷积神经网络的异常检测[J]. 清华大学学报(自然科学版),2019,59(07):523-529.
[18] ISLAM M M,LAM A,FUKUDA H,et al. An intelligent shopping support robot:understanding shopping behavior from 2D skeleton data using GRU network[J]. Robomech Journal,2019,6(1):18-29.
[19] ZHANG Y,WANG X,FRIEDMAN E G. Memristor-based circuit design for multilayer neural networks[J]. IEEE Transactions on Circuits and Systems I:Regular Papers,2017,65(2):677-686.
[20] 李丹丹,杨灿. 基于GPU并行的功能脑网络属性分析方法[J]. 计算机工程与设计,2017,38(06):1614-1618.

