一种电力负荷预测混合模型研究
田珂 丁博 马文栋 赵卫华 王坤


摘 要:为了提高短期负荷预测(STLF)的精度问题,采用了新的信号分解和相关分析技术,结合改进的经验模态分解法(IEMD)将负荷需求时间序列分解为若干个规则的低频分量。为了补偿信号分解过程中的信息损失,通过使用T-Copula进行相关分析来合并外部变量的影响。通过T-Copula分析,可从风险值(VaR)得出峰值负荷指示二进制变量,以提峰值时间负荷预测的准确性。将IEMD和T-Copula得到的数据应用于深度置信网络(DBN)来预测特定时间的未来负荷需求。
关键词:短期负荷预测;经验模态分解;T-Copula;峰值负荷;风险值;深度置信网络
中图分类号:TP348 文献识别码:A
A Hybrid Model for Power Load Forecasting
TIAN Ke1 ,DING Bo2,MA Wen-dong1,ZHAO Wei-hua2,WANG Kun2
(1.State Grid Henan Electric Power Company,Zhengzhou,Henan 450000,China;
2. Customer Service Center,State Grid Henan Electric Power Research Institute,Zhengzhou,Henan 450000,China)
Abstarct:In order to improve the accuracy of short-term load forecasting (STLF),this paper uses new signal decomposition and correlation analysis technology,combined with improved empirical mode decomposition (iemd) to decompose the load demand time series into several regular low-frequency components. In order to compensate for the information loss during signal decomposition,T-Copula is used for correlation analysis to merge the effects of external variables. Through T-Copula analysis,the binary variable indicating peak load can be obtained from the value of risk (VaR) to improve the accuracy of peak time load forecasting. The data from IEMD and T-Copula are applied to deep confidence network (DBN) to predict future load demand at a specific time.
Key words:short-term load forecasting;empirical mode decomposition;T-Copula;peak load;VaR;DBN
電力负荷预测是电力系统的重要组成部分。根据时间跨度,负荷预测通常可以分为短期负荷预测(STLF)[1]、中期负荷预测(MTLF)[2]和长期负荷预测(LTLF)[3]。目前,国内外学者对负荷预测问题进行了广泛的探索,通常可分为基于机器学习理论的智能预测方法和基于时间序列预测原理的经典预测方法。其中,智能预测方法包括神经网络[4]、极限学习机[5]、专家系统[6]等。智能预测方法预测效果好,理论值高,但实际操作较差,泛化能力较弱,容易受到数据和实验设备等因素的影响。与经典预测方法不同,智能预测方法中的经验模态分解法(EMD)可以利用历史负荷数据进行建模,并且具有所需数据少、建模理论完备、可操作性强的特点[7]。
为了缓解传统EMD的端点效应和包络拟合限制,文献[7]提出了改进的经验模式分解(IEMD)方法。为了补偿信号分解过程中的信息损失,本文引入T-Copula相关分析技术,将天气因素(即外生变量)的影响纳入到信号分解中。利用IEMD对电力负荷需求时间序列进行分解,引入系统负荷与外部输入变量的相关性分析,提高峰值时段负荷预测的准确性,通过合适的模型分别预测这两个分量,将各分量的预测结果相加得到最终的预测结果。
1 短期负荷预测(STLF)
如果一天内的电力负荷曲线定义为Em(t) = [Em(1),…,Em(N)]T ,其中,Em(N)是第m天的负荷曲线,t = 1,…,N表示不同的时间实例。STLF模型的任务是预测未来时间实例的负荷分布,即Em(t+1)或Em+1(t)。为了避免以后出现符号复杂性,将使用E(t)作为负荷需求时间序列,而不是特定日期Em(t)的负荷分布。提出的STLF混合模型的框架如图1所示。
该STLF混合模型的基本体系结构由负荷需求时间序列分解和借助相关性分析处理的外部输入变量组成,负荷需求时间序列和外部输入变量并行处理。与文献[8]相比,IEMD的应用将提高信号分解效率,并将峰值负荷指示变量作为输入参数,可提峰值值负荷时段的负荷预测精度。根据T-Copula相关分析计算出的风险值(VaR),确定每个外部输入的二元峰值负荷指示变量。
使用IEMD进行信号分解将产生固有模式函数的低频分量,如(IMFi)和信号单调函数(残差函数)。根据信号分解进行负荷预测的步骤如下:
步骤1:利用IEMD将电力负荷需求时间序列分解为具有不同频率的子序列,即固有模式函数(IMFi)和残差。
步骤2:将每个IMF和残差作为DBN输入,并获得每个IMF和残差的预测结果。
步骤3:对每个DBN获得的输出进行平均加权,然后合计得到输出1。
当通过T-Copula处理外部输入变量时,Gumbel-Hougaard Copula计算电力负荷需求与四个外部输入变量(如干球温度、湿球温度、露点温度和湿度)之间的上尾相关性。
步骤1:计算上尾相关参数λu = [λ1,λ2,λ3,λ4]和串联参数,即每个变量的VaR1,VaR2,VaR3,VaR4。然后,根据每个变量确定每个外部变量的峰值负荷指示性变量。
步骤2:使用负荷需求、相关参数和峰值负荷指示变量对每个DBN模型进行预训练。针对每个外部变量获得预测结果
步骤3:从每个DBN获得的输出进行加权平均,然后合计得到输出2。
2 负荷需求时间序列信号分解
现有信号分解方法有传统小波变换、离散小波变换、EMD等。与传统的小波变换相比,EMD适用于非平稳和非线性时间序列。然而,EMD还需要控制端部效应和包络拟合等问题。IEMD是对传统EMD的改进,其方法是:(1)结合线性外推法确定端点极值,使拟合包络包含给定的数据集;(2)采用非均匀有理B样条曲线拟合包络代替三次样条曲线处理复杂信号。
2.1 传统的经验模态分解
EMD是一种迭代移位过程,它将信号分解成不同振幅的规则低频分量。低频分量包括IMF和残差函数。IMF的性质如下:
(1)对于单个IMF,整个IMF长度的极值和过零点的个数应等于或小于1。
(2)在任何数据位置,由局部极值定义的包络线的平均值为零。
为了满足这两个性质,本文给出了从给定信号E(t)中提取IMF的迭代移位过程:
(1)确定电力负荷需求时间序列E(t)的局部极大值(Emax(t))和局部极小值(Emin(t)),并利用三次样条曲线连接上、下包络来构造局部最大值和局部极小值。
(2)确定两个包络线的平均值与原始负荷需求时间序列之间的差异。如果上下包络线的平均值表示为g1(t),且E1(t) & g1(t)之间的差定义为d1(t),则
d1(t) = E(t) - g1(t) (1)
为了成为IMF,d1(t)必须遵守上述IMF的属性。当d1(t)满足IMF的条件时,就将其选为第一个IMF的I1(t)。否则,重复上述步骤。
(3)从原始电力负荷需求时间序列中减去第一个IMF,以确定剩余r1(t):
r1(t) = E(t) - I1(t) (2)
(4)残差r1(t)可视为经过上述移位处理的新数据。重复上述过程,直到残差时间序列r1(t)是单调函数,即残差数据足够小以至于没有转折点。
(5)通过使用EMD,原始电力负荷可以表示如下:
E(t) = ■Ii(t) + rn(t) (3)
在這个迭代移位过程之后,数据可以用IMF和残差函数来表示。
2.2 传统经验模态分解的问题
即使EMD比其他传统分解技术(如小波变换或离散小波变换)更有效地分解复杂时间序列,但EMD与以下问题相关:
(1)传统EMD的末端效应会导致数据两端出现发散现象。信号的末端极值无法确定为最大值或最小值,它使包络变形并影响EMD分解。
(2)与传统EMD相关的三次样条拟合会导致超调和欠调现象。因此,得到的包络并不完整,因此会反映到提取的IMF中。
2.3 改进的经验模态分解
为了控制传统EMD的端点效应和包络拟合限制,利用改进的信号分解技术(IEMD)抑制端部效应和包络拟合限制:
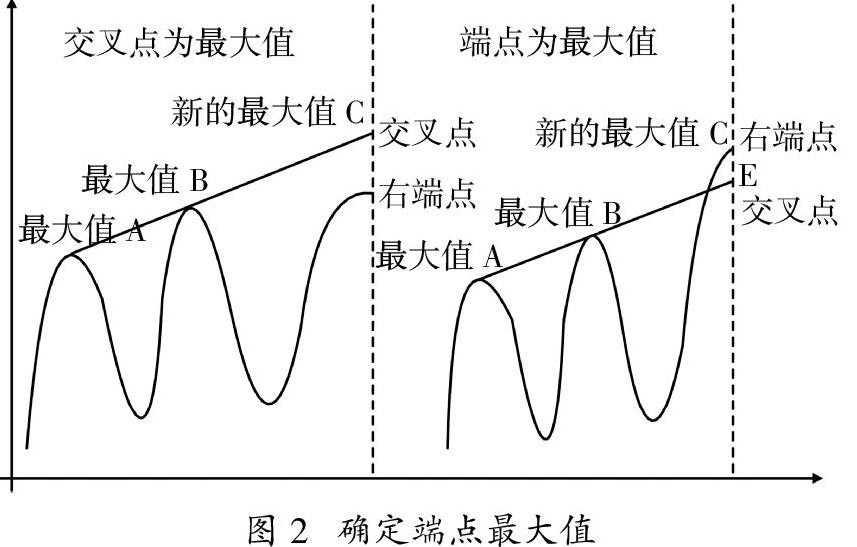
(1)抑制端点效应:为了抑制端部效应并实现真正有效的分解,采用线性外推方法确定信号的端点,使拟合包络包含给定的数据集。为了形成一个包含所有信号数据的完整包络,必须对信号的端点进行处理。此方法确定上包络拟合的端点的过程如图2所示。
两个最大值A和B最接近端点。直线AB线性延伸到终点C。如果点C小于信号的端点值E,则将点E视为是上包络拟合的新的最大值。否则,如果点C大于端点值点E,则将点E视为是上包络交叉点的新的最大值。同理,可以确定下包络拟合的端点。
(2)抑制包络拟合的局限性:文献[9]提出的原始EMD算法利用三次样条函数拟合信号的上、下包络,然后计算拟合上、下包络的平均值。由于三次样条曲线拟合计算简单,但三次样条曲线拟合会产生超调和欠调现象,使包络拟合偏离实际信号包络并形成不完全包络。
采用非均匀有理B样条(NURBS)曲线拟合方法对信号的上、下包络进行拟合得到平均包络。采用累加弦长参数化算法实现NURBS曲线拟合。与通过三次样条函数拟合包络相比,相同的仿真信号使用NURBS曲线可以拟合包络。IEMD算法可以将信号分解为不同的频率分量,不存在模式混合。
3 T-Copula分析
电力负荷与外部输入变量之间存在较高的尾部相关性。Gumbel-Hougaard-Copula模型计算了电力负荷与四个外部输入变量之间的尾部相关性。经典的二元Gumbel-Hougaard模型可以定义为:
f (x1(t),E(t)) = CP [ f x1(x1(t)),fE(E(t))]
(4)
其中,f x1(x1(t))和fE(E(t))表示边际累积分布函数,x1表示外部输入变量,E表示系统负荷需求,f (x1,x2)是二维联合分布函数,CP(x1,E)是Copula函数。确定每个外部变量的尾部相关参数:
CP(x1,E) = exp{-[(-ln x1)α + (-ln E)α]1/α}
(5)
最大似然法可用于确定Copula模型的参数 。对于系统负荷需求与外部输入变量的非线性关系,采用基于样本的累积分布函数(CDF)经验实现典型最大似然(CML)方法。CML的目标表示为:
■ = arg min - ■ln f (x1(t),E(t)) (6)
其中,N表示外部输入变量的数量。Gumbel-Hougard Copula的尾部相关参数λ1由下式给出:
λ1 = 2 - 21/α (7)
按照这种方法,可以为每个外部输入变量确定所需的Copula参数。由于电力负荷数据的波动性和多样性,对峰值负荷进行有效的统计估计至关重要。引入VaR的阈值参数来确定每个变量的峰值负荷指示变量。基于VaR计算的峰值负荷指示变量有助于提高负荷预测的准确性。由于外部输入变量是随机的,并且对电力负荷有影响,根据以下公式确定了VaR:
VaR1p = CP -1[ f (x1(t),E(t))] (8)
其中,VaR1p表示外部输入变量和系统负载的二元分布的第p个百分位数。因此,峰值负荷指示变量的二进制值由以下公式确定:
M(x1) = 1,x1(t) ≥ VaR1p0,x1(t) < VaR1p (9)
其中,M(x1)表示外部变量x1的峰值负荷指示变量,并且p的值设置为0.95。将对每个外部输入变量重复这个过程,即需要对四个外部输入变量进行四次计算。
Gumbel-Hougaard Copula模型拟合了系统负荷与外部气象变量之间的尾部相关性。显着性的默认值设置为0.05,并且通过最大似然估计来估计模型参数。
4 深度置信网络
分治算法是将问题递归分解为两个(或多个)相同(或相关)类型的子问题。该方法通过IEMD将电力负荷需求数据分解为多个IMF和一个残差。在相关分析中,可以得到了尾部相关参数和峰值负荷指示变量。将IMF、残差、尾部相关参数、峰值负荷指示变量和系统负荷的数据应用于深度置信网络(DBN)。其中,DBN具有一个无监督子部分,该子部分由多个受限玻尔兹曼机(RBM)和一个监督部分组成,监督部分是逻辑回归层,即ANN。因此,使用DBN进行学习是半监督学习。文献[10]提出的DBN为训练置信网络模型方法,即逐层贪婪预训练算法。
DBN预训练程序将多层神经网络(MLP)中的每个连续层对视为RBM[11],其联合概率定义为:
Ph | v(h|v) = ■·e■ (10)
其中,h表示应用于隐藏层的输入,v表示从可见层获得的输出,W表示隐藏层的神经元权重,a表示激活。对于每个RBM都有一对隐藏层和可见层。对于应用于具有第二偏置向量b和归一化项Zh,v的二进制v的高斯伯努利RBM:
Ph | v(h|v) = ■·e■ (11)
对于应用于连续变量v的高斯伯纳利RBM[12]。在这两种情况下,条件概率Ph | v(h|v)具有与MLP层中相同的形式。RBM的目标函数为:
L(a,b,W) = ∑log Ph | v(h|v) (12)
分层预训练方法要求DBN遵循目标函数的随机梯度下降法进行预训练。梯度法表明,参数(如a,b,W)是基于目标函数公式(12)的梯度进行更新。概率分布函数的梯度可以用以下方式表示:
■ = < vi hi > Ph | v(h|v) - < hi vi > recon (13)
■ = < vi > Ph | v(h|v) - < vi > recon (14)
■ = < hi > Ph | v(h|v) - < hi > recon (15)
其中,< hi > Ph | v(h|v)是相對于输入原始数据的条件分布的期望,< hi vi > recon是第i步重构分布的期望。使用对比发散通过交替的Gibbs采样来获得重构分布的期望值[13]。则更新公式如下:
Wi+1 = Wi + η(< vi hi > Ph | v(h|v) - < hi vi > recon) (16)
ai+1 = ai+η(< vi > Ph | v(h|v) - < vi > recon) (17)
bi+1 = bi+η(< hi > Ph | v(h|v) - < hi > recon) (18)
为了训练多层,可以训练第一层并将其冻结,然后将输出的条件期望用作下一层的输入并继续训练下一层。基于分层的预训练方法,对DBN算法的所有参数进行初始化。以监督的方式对这些参数进行调整,直到DBN的损耗函数达到其最小值[14]。最后,将反向传播算法应用于微调过程。所有参数均从上到下更新,从而减少了预测误差。
由于气候和社会活动的影响,电力负荷数据主要表现为日、周、年三个周期。假设时间序列数据集为E = Et ∶ t∈T,其中T是索引集。滞后k自相关系数rk可以通过表示为:
rk = ■ (19)
其中,■是给定时间序列中所有E的平均值,rk表示度量时间t和k处时间序列的线性相关性。
5 仿真分析
5.1 数据集描述
在国网河南省电力公司电力科学研究院数据集上验证了所提出的混合负荷预测模型。数据集包括三组主要的测量变量:天气数据(即干球温度、湿球温度、露点温度和湿度)、时间分类数据(即小时、月、日)、社会数据(即工作日、周末、假日)和特定采样时间的电力负荷需求。
5.2 性能评估标准
相对于平均绝对百分比误差(MAPE)和均方根误差(RMSE),比较了所提出的负荷预测模型的性能
(1)MAPE定义为:
MAPE = ■■■ × 100 (20)
其中,E(t)表示实际负荷需求,■(t)表示预测负荷需求。
(2)RMSE定义为:
RMSE = ■ (21)
MAPE和RMSE值越小,预测精度越高。
5.3 实验结果
所有仿真都是在Matlab上进行,并对两个算例进行了验证。对于案例研究,使用以下公式将数据集线性缩放为[0,1]:
Ei = ■ (22)
在案例研究中,数据采集日期为2018年1月1日至2018年12月31日,采样时间为半小时。将全年数据分为四个季节:(1)1月至3月,(2)4月至6月,(3)7月至9月,(4)10月至12月。将一个月的三周数据集作为训练数据集,剩余一周作为测试数据集。信号分解得到的输入数据集为8个IMF和残差信号。利用自滞后相关,将这些分解后的信号应用于电力负荷预测。从相关性分析中获得的输入数据集包括尾部相关参数、二元峰值指示变量和根据学习环境设置的负荷需求数据集,这些数据集应用于DBN进行外部变量的负荷预测。为了公平比较,在2018年的每个月中,都将三周负荷需求数据集视为训练数据集,剩余一周视为测试数据集。这意味着目标是预测一周的负荷需求。对于每个季节,考虑了两个月的数据集来评估所提出方法的负荷预测性能。因此,在两个月内,预测了两周的负荷需求。
为了预测电力负荷需求,汇总了信号分解和相关分析结果。考虑了相等的加权平均值来确定最终的预测负荷需求。2018年1月至3月河南郑州的模型预测电力负荷需求结果,如图3所示。
由图4可见,峰值负荷时间内负荷预测精度有所提高。从平均误差分布结果可以看出,峰值时段的负荷预测精度有所提高,这将有助于电力运营商制定合理的发电计划和配电维护计划。为了与文献[16]中的结果进行比较,对河南省其他5个地市进行了模拟,如表1所示。
由表1可见,负荷预测结果的误差,即所提出模型的MAPE和RMSE值低于文献[16]中的其他比较模型。与文献[16]相比,该模型的MAPE值降低了21.19%,RMSE值降低了16.93%。性能提高的原因是:(1)IEMD提高了信号分解效率;(2)T-Copula通过计算Var中的峰值负荷指示性变量,有助于提高峰值时段的负荷预测精度。
6 结 论
针对电力负荷预测问题,提出了一种新的混合STLF模型。利用IEMD对电力负荷需求时间序列进行分解,引入系统负荷与外部输入变量的相关性分析,提高峰值时段负荷预测的准确性,通过合适的模型分别预测这两个分量,将各分量的预测结果相加得到最终的预测结果,利用电力负荷数据集验证了该模型的有效性。
参考文献
[1] 杨照坤,宋万清,曹琨. 基于量子遗传算法的FARIMA模型電力负荷短期预测[J]. 传感器与微系统,2019,(10):143-145.
[2] 何耀耀,秦杨,杨善林. 基于LASSO分位数回归的中期电力负荷概率密度预测方法[J]. 系统工程理论与实践,2019,39(07):1845-1854.
[3] 张建寰,吉莹,陈立东. 深度学习在电力负荷预测中的应用[J]. 自动化仪表,2019,40(08):8-12.
[4] 张小军,吴标,孙帆,等. 一种基于数据挖掘技术的电力负荷预测算法研究[J]. 自动化技术与应用,2018,37(12):7-11.
[5] 胡函武,杨英,施伟,等. 一种基于极限学习机的短期负荷预测方法[J]. 黑龙江电力,2018,40(06):471-476.
[6] 张超,陈杰睿,冯平. 基于混沌理论的电力系统负荷预测应用[J]. 计算机与数字工程,2018,46(11):2165-2169.
[7] 肖白,房龍江,李介夫,等. 空间负荷预测中确定元胞负荷最大值的经验模态分解方法[J]. 东北电力大学学报,2018,38(03):8-14.
[8] MOHAMMADI M,TALEBPOUR F,SAFAEE E,et al. Small-scale building load forecast based on hybrid forecast engine[J]. Neural Processing Letters,2018,48(1):329-351.
[9] LI H,WANG C,ZHAO D. Filter bank properties of envelope modified EMD methods[J]. IET Signal Processing,2018,12(7):844-851.
[10] CHENG W,SUN Y,LI G,et al. Jointly network:a network based on CNN and RBM for gesture recognition[J]. Neural Computing and Applications,2019,31(1):309-323.
[11] 王志明,张航. 融合多层卷积神经网络特征的快速图像检索方法[J]. 计算机辅助设计与图形学学报,2019,31(08):1410-1416.
[12] 张光荣,王宝亮,侯永宏. 融合标签的实值条件受限波尔兹曼机推荐算法[J]. 计算机科学与探索,2019,13(01):138-146.
[13] COHEN J D,LI L,WANG Y,et al. Detection and localization of surgically resectable cancers with a multi-analyte blood test[J]. Science,2018,359(6378):926-930.
[14] 吴坚,郑照红,薛家祥. 深度置信网络光伏发电短时功率预测研究[J]. 中国测试,2018,44(05):6-11.
[15] QIU X,REN Y,SUGANTHAN P N,et al. Empirical mode decomposition based ensemble deep learning for load demand time series forecasting[J]. Applied Soft Computing,2017,54:246-255.
[16] QIU X,SUGANTHAN P N,AMARATUNGA G A J. Short-term electricity price forecasting with empirical mode decomposition based ensemble kernel machines[J]. Procedia Computer Science,2017,108(2):1308-1317.

