找突破点与生长点促进初中学生数学思维的发展

周秀丽

摘要：数学思维的过程是要经历疑惑、解惑、反思、重构的思维过程，是一种探索的过程，是活跃的、动态的过程。但现在由于培训班的盛行，大家都显得急功近利，过多地接触到了接受式、灌输式的学习方式，喜欢吃“速食知识”“现成结论”，这其实是阻碍了数学思维的发展。本文在实例中分析如何找到问题的突破点与生长点。

关键词：初中学生；数学思维；突破点；生长点

中图分类号：G633.6文献标识码：A文章编号：1992-7711（2020）04-0055

数学核心素养是囊括了数学知识、数学能力、数学过程、数学经验、数学思维、数学情感的一个数学认知共同体，是数学品质的集中体现。作为教师，我们应该多放手让学生去互动、去探究，找到问题的突破点和知识的生长点，促进学生思维的发展。可以引导学生利用颜色标记、结论倒推来说一说题目解决的突破点，利用前后相似内容或知识点的联系说一说其中的疑点与知识生长点。

一、众人拾柴，说突破点

学生某道题做不出来，往往是因为在某个点被卡住了，我们称之为突破点。只要找到这个突破点，后面的问题迎刃而解。

比如题目：按如图将？ABCD纸片沿着EH、EF、FG、GH向内部折叠，恰好折叠成一个叠合矩形EFGH，若EF=5，EH=12，求AD的长。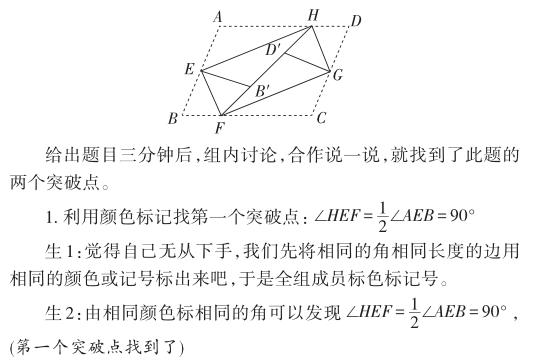

生3：再加上条件：若EF=5，EH=12，那么就得出HF=13.

2.利用卡点倒推找第二个突破点：∠EB′F=∠GD′H

接着利用综合分析法将已知条件顺推，要求目标倒推，对比着寻找连接点。

生4：记B点翻折后的位置為B′，记D点翻折后的位置为D′，由于矩形EFGH中EF//HG，所以∠GHF=∠EFH，同时EF=HG，

生5：卡住了，猜想△B′EF≌△D′GH

生4：但是除了∠GHF=∠EFH，EF=HG，还缺一个条件，

组员们都找不到第三个条件促使△B′EF≌△D′GH。

生1：那就从其他边或角找一找。

生2：∠EB′F=∠GD′H （第二个突破点找到了），

生4：为什么？

生2：因为∠EB′F=∠B′=∠D′=∠GD′H

生3：所以由∠EB′F=∠GD′H，∠GHF=∠EFH，EF=HG得出△B′EF≌△D′GH，得出B′F=D′H，

生5：所以DH转化为D′H再转化为B′F，而由于折叠，AH可以转化为B′H

生1：那就是说把AD转化成AH+HD，再转化成B′H+B′F，即HF。

生4：之前已求得HF=13，所以AD=13。

通过同伴的通力合作，利用颜色标记、利用卡点倒推找到了此题的两个突破点，这两个突破点直接切中要害使后续的解题能够顺畅进行。生生合作，你一言我一语，将题目的层层面纱揭开，一起完成说题。然后再一人将整道题说一说，就是把思维理顺，将隐藏在思维中的盲点暴露出来，思维逐渐变得清晰。通过合作，让学生在学习过程中体验“众人拾柴火焰高”的数学味道，激发学生数学学习探究的欲望。

二、化零为整，说疑点、生长点

目前，很多学生能够按照教师说的方法进行解决问题进行操作，但是他们其实还存在比较多疑惑的，只是没有质疑解惑的习惯。结果就是学习中只会照样画葫芦，没有主见，更无法进行深层次的学习。

所以在可能的疑点处，教师要鼓励学生去说一说为什么。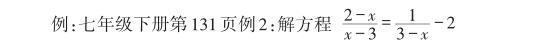

师：为什么这个分式方程会产生增根？为什么增根要去掉？

生1：原分式方程中有这个限制：分母是不能为零的，整式方程没有这个限制，相当于条件放宽了，所以根可能就会多起来。

生2：以上方程两边同时乘以（x- 3），化成整式方程2-x=-1-2（x-3）。而原分式方程中分母是不能为零的，即未知数不能为3，而转化后的整式方程中没有这个限制，结果算得整式方程的根可以为3，那么分式方程转化成整式方程多出来这个根3。

生3：我觉得他俩讲得都有道理，但我要补充我的理解：这个为什么叫增根？从原分式方程化到整式方程，条件放宽了，就增加了根，所以叫增根。（其他学生频频点头，该生的话形象好理解）

生4：这个多出来的增根是由整式方程2-x=-1-2（x-3）算得的，所以必定是该整式方程的根，但不一定是原分式方程的根，当这个根3代入原分式方程使得分母为零，方程就没有意义了，所以3不是原分式方程的根，所以要去掉。

学会质疑，是学习数学的一个重要品质。只有学生敢于质疑才能让他们自己真正思考起来，在质疑中努力思考，说一说疑点，说一说如何解开疑点，这样才能在学习中有自己的主见，一通百通，才能进行更深层次的学习。而目前我们在教学中经常会发现一些学生只会死记书上结论，在实际问题中又不会灵活运用，这是因为对知识内容结论的不理解，不知其所以然。因此，我们有必要引导学生关注知识或结论的形成过程，多问一个为什么，放慢脚步，让学生找一找、说一说、争一争、辩一辩，找到问题的突破点与知识的生长点，促进其数学思维的发展。

（作者单位：浙江省温州市南浦实验中学325000）