Simulink应用以及傅里叶变换MATLAB仿真

孙慧萍，秦 坤，李 静

（ 1.山西大同大学物理与电子科学学院，山西大同037009；2.天津工业大学电子与信息工程学院，天津300387）

高校教育一般分为理工、文史、医学等等。MATLAB作为高校工科生的必学课，在当今的高等教育中起着非常重要的作用。随着计算机在人们日常生活、学习、娱乐以及研究中的应用越来越普遍，计算机语言也就应运而生。本文主要研究了MATLAB 中的Simulink 组件、应用以及傅里叶变换MATLAB仿真。

1 Simulink简介

对于高校中的工科类学生来说，经常会用很多软件进行大量的仿真实验。MATLAB 软件是其中应用很广泛的软件之一，它可以帮助大家学习很多知识理论[1]。Simulink 是MATLAB 中最重要的组件之一，它可以实现建模和仿真。人们应用MATLAB来编写程序，程序一般都非常长。而Simulink的操作则是更为简单的，它只需要通过鼠标拖动Simulink 工具箱中已有的程序，并将其连接就可以实现信号的输出，结果清晰易懂[2-3]。例如，利用Simulink 输出正弦信号。首先，在Simulink 的工具库中拖出正弦信号与示波器如图1所示：

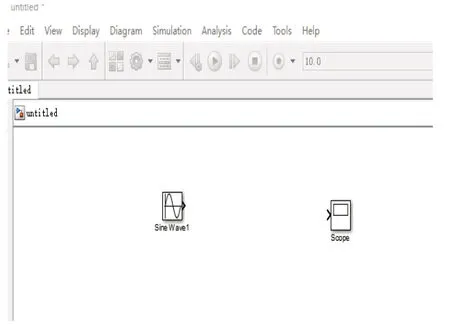
图1 模型图

然后，直接用鼠标拖拽箭头将两个器件连接起来，运行之后，双击示波器即可以出现波形，运行结果如图2所示：

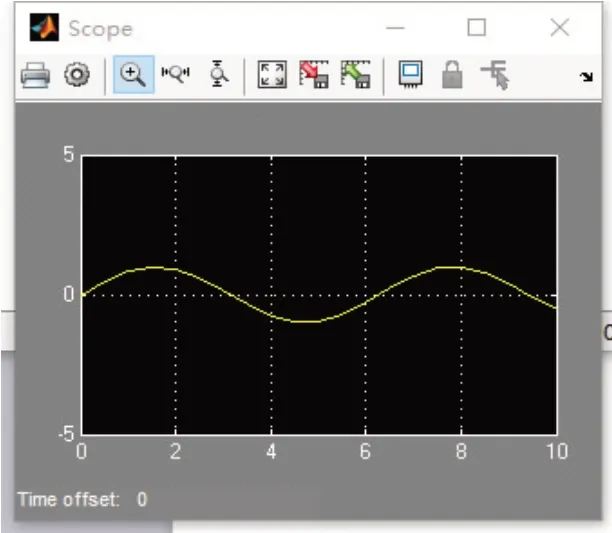
图2 运行结果

图2 是最为简单的连续正弦信号的仿真结果。但是，Simulink并不能对离散信号进行仿真。

2 Simulink应用

Simulink的应用很多，还可以用来创建系统，对系统所对应的微分方程进行求解，并绘制其波形[4-5]。例如：对微分方程d2y(t)/dt2+dy(t)/dt+y(t)=u(t)进行求解的模型图如图3所示：

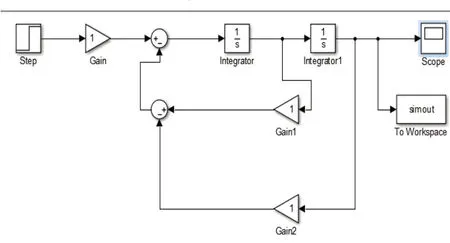
图3 模型图

当u(t)等于108时，仿真结果如图4、图5所示：

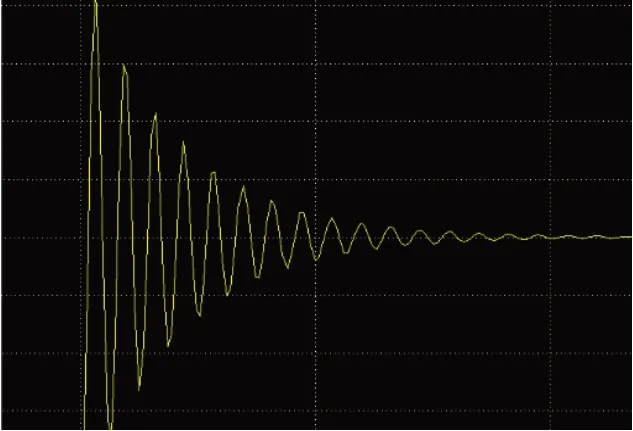
图4 仿真结果

图5 仿真结果

通过上面的仿真，可以明显的看出利用Simulink 这一组件很容易就可以仿真出《信号与系统》这门课程中的微分方程。这样可以通过Simulink这个组件来帮助学习类似《信号与系统》这门课程的课程。可见，Simulink对于人们的学习是非常有帮助的。

所以，当在学习类似《信号与系统》这门课程时，可以最大限度地利用MATLAB 这一软件帮助学习。MATLAB 中还有许多其他组件，都可以在一定程度上帮助人们对于系统进行理解。所以，MATLAB 在高校理工科的教学过程中起到了巨大的作用。

3 MATLAB在离散系统中的运用

在日常生活中，常常提到的信号包括模拟信号、离散信号。一般用x(t）来表示模拟信号，变量t代表的是时间。离散信号用x(n)表示，其中变量n为整数，并代表时间的离散时刻（离散时间信号）。离散信号可以表述为：

通常在MATLAB 中，用向量x来表示一个长度有限的序列。但是用一个向量来表示序列的时候，就没有包含基准采样位置的信息。因此，要完全地表示x(n)就要用x和n两个向量。序列x(n)={2,1,-1,5,1,4,3,7}, 在MATLAB 中就表示为下面的式子：

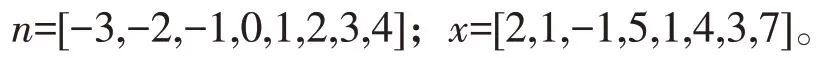
因为内存是有限的，所以MATLAB 无法表示无限序列。

4 离散傅里叶变换的MATLAB实现

傅里叶变换是离散时间系统的许多变换域方法中的一种。利用MATLAB 软件对离散傅里叶变换进行仿真，结果如下：

例如：计算离散傅里叶

解：设有限序列xn(n)的长度为Nx，则按定义，求其N点傅里叶变换Xk(k)的程序为

clear,

xn=input('x=')；Nx=

length(xn)；N=Nx %取N为x的长度

tic,n=[0：1：N-1]；k=[0：1：N-1]； %设定 n 和 k 的行向量

WN=exp(-j*2*pi/N)； %WN为因子

nk=n'*k；%产生一个含nk值的N*N维矩阵

WNnk=WN.^nk； %换算矩阵

Xk=xn*WNnk；toc

%DFT系数向量，离散傅里叶变换的结果

plot(abs(Xk)),grid %绘制幅频特性图

当N 非常大时，运算速度比较低。这时可直接调用fft（快速离散傅里叶变换的函数），其调用式格式为X=fft（x,N）。

其中：x 是输入的时间序列，N 是傅里叶变换的点数。若省略N，则自动把x 的长度作为N。当N 取2的幂时，变换速度最快，要提高fft 函数的运行速度，程序应编写为：

xn=input('x=')；Nx=length(xn)

%取N为大于Nx而接近于Nx的2的幂

N=pow2(nextpow2(Nx))；

tic,X=fft(xn,N)；toc

Nx＜N, x长度不足N的部分，会自动补0。

输入 x=sin(0.1*[1：700])+randn(1,700)；

即最后程序为：

clear,

xn=input('x=')；Nx=length(xn)

%取N为大于Nx而接近于Nx的2的幂

N=pow2(nextpow2(Nx))；

tic,X=fft(xn,N)；toc

plot(abs(X)),grid

仿真结果如图6所示：

图6 信号的fft的振幅频率特性

图6为利用快速傅里叶变换对信号进行仿真的振幅频率特性。图中横坐标为频率，纵坐标为振幅，两个较高的脉冲为有效信号，其余为噪声。整个频谱图大体上为对称图形，并以Nyquist 频率为对称轴。根据该频谱图可以很好地区分有效信号、噪声。

4 总结

本文先简单介绍了MATLAB 中的Simulink 组件，并以正弦信号为例，介绍了其仿真过程，最后用MATLAB 仿真离散傅立叶变换，结果很理想，为以后的研究奠定了一定的基础。