关于有效估计的一点讨论

李秀兰

（山西大同大学数学与统计学院，山西大同037009）

参数估计是数理统计的一个重要内容，无偏性是对估计最常见的合理性要求，直观的想法是希望该估计围绕参数真值的波动越小越好，波动大小可以用方差来衡量[1-2]。

定义1对参数估计问题，设是q的一个无偏估计, 若对θ的任一无偏估计,都有θ≤Var(), ∀θ∈Θ ,则称是q的(一致)最小方差无偏估计,记UMVUE。

一致最小方差无偏估计是所有无偏估计中方差最小的, 在无偏性和有效性两个标准下是最好的。

(1)Θ 是开区间；

(2)支撑S={x：p(x,θ)＞0}与θ无关；

(4)对p(x；θ)积分与微分运算可交换

定理1(C-R 不等式) 设总体X的概率函数p(x；θ)满足定义 2 的条件(1)～(5),T=T(X1，…，Xn)是g(θ)的任一个无偏估计,g′(θ)存在，且对一切q，对

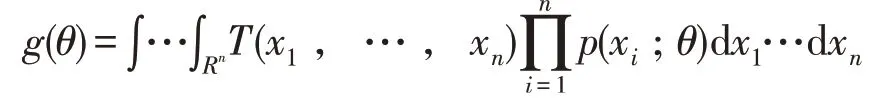
的微商可在积分号下进行（对离散总体，将积分号改为求和符号），则有

其次，会计信息化依靠着网络系统来运行，一旦系统出现故障问题，企业的财务信息和数据便会泄露，使得企业面临着严重的经营风险，降低企业的经营效益。所以企业应当针对财务系统建立起全面地监查制度，实施对于财务系统设备的管理与监控工作，形成系统化、规范化的信息数据处理工作，提高企业财务信息数据的安全性。

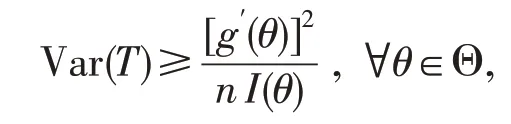
称[g′(θ)]2/[nI(θ)]为g(θ)的无偏估计的方差的C-R下界,简称C-R下界。

特别当g(θ)=θ,为q的无偏估计时,C-R不等式简化为

C-R 不等式表明,一定条件下, 无偏估计的方差不能任意小。

定义3若C-R 不等式中等号成立, 则称T是g(q)的有效估计。

显然有效估计一定是无偏估计、相合估计、UMVUE。

例1X～b(1,p),(1)求p的有效估计；(2)求θ=p2的UMVUE,这个估计是不是有效估计？

解(1)p(x；p)=px(1-p)1-x,x=0,1。先验证C-R不等式的条件成立。

参数空间Θ=(0,1)为开区间；支撑S={0,1}与p无关；

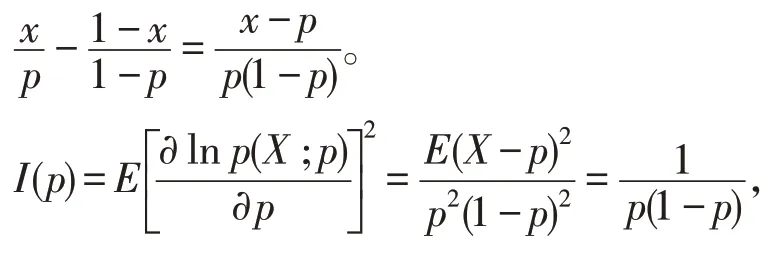
那么p的无偏估计的C-R下界为而是p=E(X)的无偏估计,且

设φ=φ(X1,…,Xn),E(φ)=0,D(φ)＜∞ 。

则(X1,…,Xn)的联合分布列为

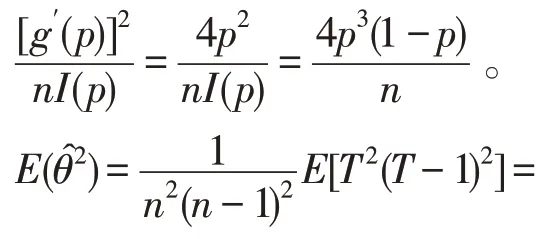
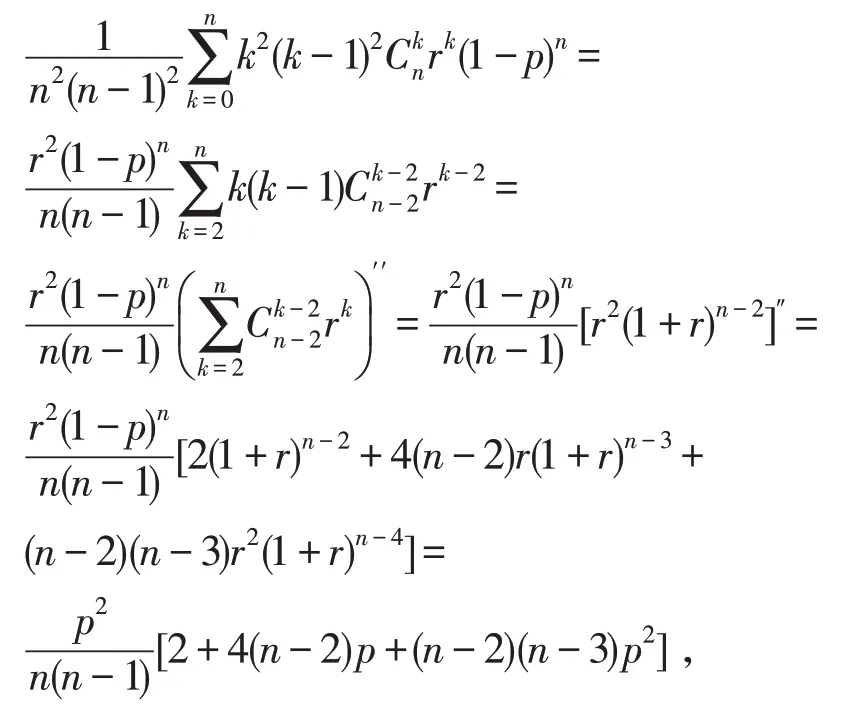
那么

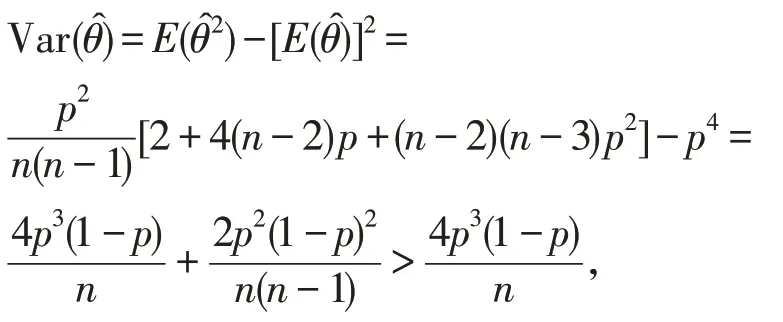
例2 设X～U(0,θ),p(x；θ)=其中0 ＜x＜θ, 已知=是θ的无偏估计。

显然分布的支撑S=(0,θ)与参数θ有关,并且

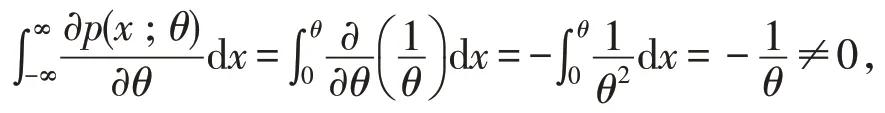
可见C-R不等式的条件不满足，所以q的有效估计不存在。但是