双层网络上的社会传播

李小林，许润杰，娄 洁，许新建

(上海大学数学系，上海 200444)

0 引言

作为社会群体，人与人之间总是不断地交流来传播信息和观点，这种人际沟通、影响、传递的过程称为社会传播。如何模拟这种人际传播是社会网络研究中的一个基本问题[1]。一般地，传播可以分为简单传播和复杂传播[2]。所谓简单传播是指任意一对不同状态个体之间传染的发生仅仅依赖一个独立参数——传染率，而与周围邻居的状态无关，从而服从泊松过程。这一假设在经典流行病研究中被广泛采用[3]，因此生物传播属于典型的简单传播。而复杂传播往往考虑局部依赖性和时间记忆性，例如一个观点如果来自于多个不同渠道，那么它更容易会被接受，因此社会传播属于典型的复杂传播。

关于社会传播的研究最早可以追溯到1973年Schelling提出的阈值模型[4]。该模型假设系统中的个体有两个状态：0和1。对于一个状态为0的个体，当其状态为1的邻居数目或比例超过一个临界值时，个体的状态也从0转变为1。以社会罢工为例，一个人是否参加罢工的阈值可以定义为其周围有多少或多大比例的人已经参加了罢工，如果这个人是激进的，那么他的理性阈值可能较低，如果这个人是保守的，那么他的理性阈值相对较高。

虽然阈值模型的研究在社会学[5]和经济学[6]中早已展开，但是直到2002年才引入接触网络[7]。Watts利用母函数方法计算了传播条件和感染规模，他发现个体的阈值差异性和结构异质性对传播起着完全相反的作用：一方面，个体的内在阈值差异性越强，观点越容易扩散，或者说系统越容易发生全局崩溃(global cascade)；另一方面，个体的外在结构异质性越强(如度的异质性)，观点越不容易扩散(no cascade)，即系统的鲁棒性越好。这一有趣的结论引起了广大研究者的兴趣，纷纷投入这一领域。一方面，研究者开始考虑更多的网络结构特征对传播的影响，如度相关[8]、集聚系数[9]、时效[10]、有向[11]等。另一方面，更多的传播机制被提出，如媒体影响力[12]、多阶段扩散[13]、个体记忆性[14]、信念坚定[15]等。在这些研究中，传播往往都是限制在单个网络上。

上述研究相对简单，无论是线下网络还是线上网络都采用Erdös-Rényi(ER)随机图[22]，没有考虑结构异质性，而实证研究早已表明绝大数的在线网络都是非均匀的[23]。鉴于这一点，本文采用scale-free(SF)网络[24]来模拟线上网络，并构造ER-SF双层网络，研究线下均匀网络与线上非均匀网络的耦合关系对社会传播的影响。

1 模型

为了研究方便，我们考虑节点一一对应的的双层社会网络。如图1所示，网络中的任意一点i(i=1,2,…,n)既有线下邻居也有线上邻居，其个数分别可以用线下度ki,α和线上度ki,β来表示。即使点i的线下度与线上度相等，其连接的邻居也未必相同。已有研究假设网络的度分布是均匀的[16-17]，即对同一层网络来说，所有节点的度值都差不多，典型模型是ER随机图[22]，其度分布满足泊松分布p(k)～zke-k/k!，其中p(k)表示单层网络中任意一点度为k的概率，z是该层网络中所有节点的平均度。使用ER模型可以较好地模拟线下网络，但是线上网络中个体的差异非常大(如度的异质性)，使用非均匀网络更恰当，典型模型是Catanzaro等人提出的SF配置网络[24]，其度分布满足幂律分布p(k)～k-γ，其中γ是控制度分布指数的参数。

图1 3种耦合网络示意图

进一步，考虑线下ER网络和线上SF网络基于度的3种耦合情况[25]：完全不相关(no correlation，简称nc)，完全正相关(maximum positive，简称mp)，完全负相关(maximum negative，简称mn)。完全不相关是指两层网络中节点度之间不存在相关性，此时整个网络节点度的联合概率分布为

(1)

完全正相关是指节点在线下网络中的度越大(或越小)则它在线上网络中的度也越大(或越小)，此时节点度的联合概率分布为

(2)

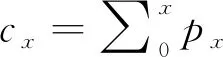
(3)

(4)

其中，μα和μβ分别表示节点在线下网络和线上网络中的理性阈值，mα和mβ分别表示节点线下邻居和线上邻居中状态为1的个数。

给定一个初始种子，传播能够进行下去的必要条件是网络中存在脆弱点。所谓脆弱点是指节点在线下网络或线上网络中只要有一个邻居处于接受状态它就会被激活，根据式(4)，相应的概率可以写为

(5)

(6)

由此，线下网络和线上网络中脆弱点度分布的母函数可定义为

(7)

(8)

进一步，在线下网络或线上网络中随机选择一条边，其连到脆弱点的概率分别为

(9)

(10)

其中zα和zβ分别表示线下网络和线上网络的平均度。传播要形成规模，则要求网络中存在脆弱分支。在网络中随机选择一点，其与脆弱分支相连的概率可定义为

(11)

其中，H1,α(x)和H1,β(x)分别表示线下网络和线上网络中随机选择一条边，其与脆弱分支相连的概率，

H1,α(x)=[1-G1,α(1)]+xG1,α(H1,α(x))
H1,β(x)=[1-G1,β(1)]+xG1,β(H1,β(x))

(12)

根据渗流理论，系统发生全局崩溃对应着脆弱巨分支的出现，即方程(12)的雅可比矩阵的谱半径大于1[16]，

(13)

其中，Jij(i,j=1,2)为方程(12)的雅可比矩阵元，即

(14)

由H0(x)的定义可知，H0(1)表示网络中随机选择一点到达脆弱小分支的概率(包括到达脆弱规模为0的情形)，因此脆弱巨分支的大小为

Sv=1-H0(1)

(15)

2 结果

对于一一对应的双层网络来说，线下ER网络和线上SF网络的规模必然相等，即Nα=Nβ=N。考虑可比性，令线下网络和线上网络的平均度相等，即zα=zβ=z。为了计算方便，规定每层网络中的个体阈值都相同，即μi,α=μi,β=μ。初始时刻随机选择一个节点作为传染源，令其状态为1，其余节点状态为0。分别在完全不相关，完全正相关及完全负相关三种耦合下的ER-SF双层网络(N=10 000)上各进行了100次蒙特卡罗模拟，计算了脆弱巨分支和崩溃条件，并同式(15)和(13)进行了对比。

当线下网络和线上网络的耦合完全不相关时，网络中点i的线下度ki,α和线上度ki,β无关(见式(1))。在给定阈值条件下，i是否被激活取决于ki,α和ki,β的大小，而对整个耦合网络来说，脆弱巨分支Sv是否出现则与平均度z密切相关。如图2a所示，圆点是网络上100次模拟的结果，实线是式(15)的理论预测，在μ=0.24条件下，当z很小时(低连通区域)，网络非常稀疏，传播无法进行。随着z的增加，Sv从0变到大于0，网络开始发生崩溃，对应的平均度临界值zl称为崩溃下界。进一步增加z，脆弱点之间连通性不断增强，导致Sv越来越大。然而，当z很大时(高连通区域)，式(5)和(6)成立非常困难，即脆弱点不断减少，网络不再发生崩溃，对应的平均度临界值zh称为崩溃上界。作为对比，ER-ER双层网络的结果也一并给出。尽管模拟结果存在一定的涨落现象，但是和理论结果(式(15))符合较好。在此基础上，图2b给出了(μ,z)双参相图，方格是网络上100次模拟的结果，实线是式(13)的理论预测。随着个体阈值μ和网络连通性z的变化，系统存在一个崩溃窗口，与式(13)的预测一致，即系统在窗口内部发生全局崩溃而在窗口外部不发生崩溃。在崩溃下界(zl≤1)，网络中大部分的节点度为0或1，线上SF网络限于度分布的异质性，其孤立点的数目比线下ER网络更多，所以ER-SF双层网络的鲁棒性优于ER-ER双层网络。在崩溃上界(zh>2)，线下ER网络的节点度值整体都会增大，脆弱点很难出现，而线上SF网络的异质性却进一步增强，一方面大量的低度节点依旧存在，可以成为脆弱点，另一方面，大度节点的数目有所增加，一旦成为种子将会促进传播，所以ER-SF双层网络的鲁棒性劣于ER-ER双层网络，这种差别随着z的增加不断增大。

图2 完全不相关耦合下的脆弱巨分支和崩溃窗口

当线下网络和线上网络的耦合完全正相关时，网络中点i的线下度ki,α越大，其线上度ki,β也越大，整个网络的联合度分布服从式(2)，仍然可以代入式(13)和(15)求出理论结果。图3给出了脆弱巨分支和崩溃窗口的计算结果，圆点和方格是网络上100次模拟的结果，实线是式(15)和(13)的理论预测。当网络的连通性很弱时，尽管每层网络都非常稀疏，但仍然存在少数度大于等于1的节点，完全正相关保证了一旦某节点在下层的度大于等于1，其在上层的度也必然大于等于1。如果这类节点在某一层的某个邻居是初始种子，那么它们很有可能成为脆弱点而被激活(见式(5)和(6))，不但会在该层继续激活其它邻居，而且会通过另一层的网络进行传播。最终这些非孤立点可能会导致一个小规模的崩溃。如图3a所示，即使在z=0.1时，无论是ER-ER网络还是ER-SF网络在正相关下都有大约9%的节点会被感染。而线上SF网络的非均匀性使得ER-SF网络略易于传播。当网络的连通性很强时，无论是哪一层网络中的节点都很难成为脆弱点。即使线上SF网络有一些小度节点成为脆弱点，一方面其线上较少的邻居数目使得传播困难，另一方面其在线下ER网络的度相对较大不易成为脆弱点，从而阻碍进一步传播，因此ER-SF网络比ER-ER网络鲁棒性更强，如图3b所示。

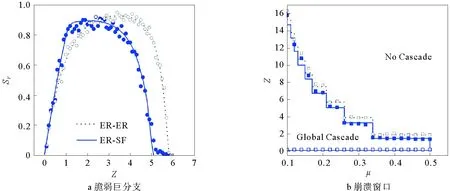
图3 完全正相关耦合下的脆弱巨分支和崩溃窗口

当线下网络和线上网络的耦合完全负相关时，网络中点i的线下度ki,α越大，其线上度ki,β却越小，整个网络的联合度分布服从式(3)，仍然可以利用式(13)和(15)算出理论结果。在低连通区域，尽管节点在某层网络的度可能为0，但是负相关耦合保证了其在另一层网络的度不为0，所以网络中线下度和线上度都不为零的节点相对较少，这将大大削弱跨层传播，传播主要依赖单层网络，脆弱点形成巨分支比较困难，不过一旦网络中出现脆弱巨分支，规模将会较大，如图4a所示。而在高连通区域，完全负相关耦合使得ER-SF网络比ER-ER网络的鲁棒性略差，如图4b所示。相对于ER-ER双层网络中脆弱点大比例减少，ER-SF网络则不同，负相关使得下层ER网络中小度节点对应上层SF网络中的hub节点，一旦这些小度节点在ER层成为脆弱点，它们在SF层的hub效应将使传播仍有可能进行下去，即跨层传播在一定程度上削弱了系统的鲁棒性。

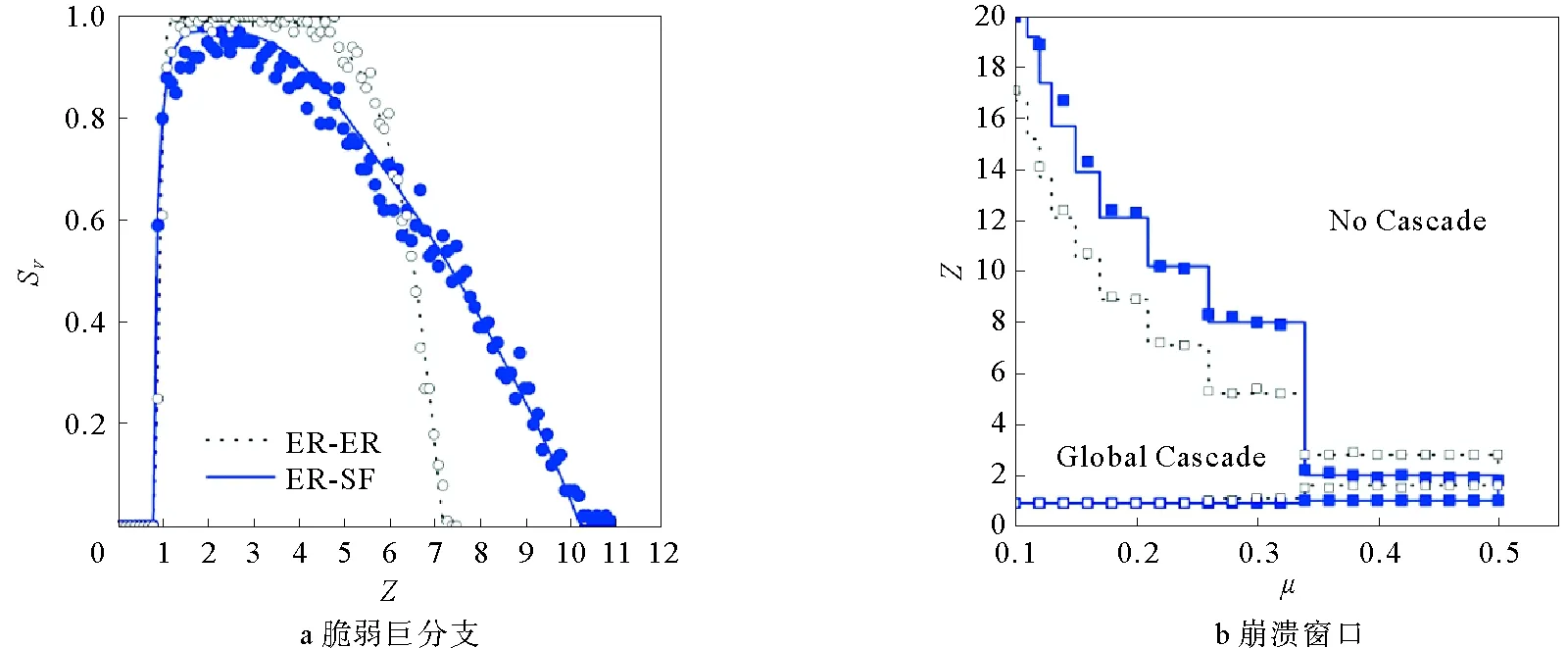
图4 完全负相关耦合下的脆弱巨分支和崩溃窗口

3 结论

自“计算社会学”[26]这一概念于2009年在科学杂志上提出以来，无论是传统的社会学家，还是数学家和计算机学家都纷纷进入这一新兴领域。如何提供新的模型和方法来解释社会现象和数据规律是一个充满挑战性的课题，而复杂网络理论是当前国际上公认的研究计算社会学的有效工具之一。

本文研究了线下ER网络和线上SF网络协同传播这一问题，比过去纯粹考虑线下线上都是ER网络更贴近实际。针对ER-SF双层网络上的阈值模型，利用母函数方法得到了系统发生全局崩溃的条件和相应脆弱巨分支的大小，并分别应用到完全不相关，完全正相关及完全负相关三种耦合情形中。与完全不相关耦合相比，完全正相关耦合在低连通区域会削弱系统的鲁棒性而在高连通区域会增强系统的鲁棒性，完全负相关耦合则会导致相反的结果。进一步，通过比较ER-SF双层网络和ER-ER双层网络在不同耦合下的崩溃结果，发现在完全正相关耦合下，ER-SF双层网络比ER-ER双层网络在低连通区域鲁棒性更差而在高连通区域则相反；在完全负相关耦合下，ER-SF双层网络比ER-ER双层网络在低连通区域鲁棒性更好而在高连通区域则相反。

上述结果是在“或”激活机制和全同阈值两个条件下得到的。一个自然的延伸是把上述理论推广到更加复杂的情形，如“与”激活机制和分布阈值的情形，但相应的计算量也大大增加。