含时滞多智能体系统的边动态二分一致性

李英桢，纪志坚，刘 帅，杨仪龙

(青岛大学自动化学院，山东 青岛 266071)

0 引言

多智能体系统研究的热点问题是其一致性，一致性是一种普遍的群集行为，在自然界中，鱼群聚集、鸟类迁徙及萤火虫同时闪光；在人类社会中，掌声的同步及人类生物振荡器的同步都可以归纳为一致性问题。一致性是多智能体实现协同合作共同完成任务的基础，其在包括群集、分布式计算、传感器网络及编队控制等许多领域都有广泛应用，如机器人编队控制、无人机协调控制以及人造卫星控制等。目前关于一致性的研究大多基于个体间的合作关系，然而在实际的问题中，如社会学，飞机编队，个体间除了合作关系，还常常存在竞争关系。关于多智能体之间的合作关系，最初R.Olfati-Saber在文献[1]中构造了基础一致性协议，在连通无向图下研究了平均一致性问题。之后W.Ren和R.W.Bread在文献[2]中提到一个解决一般一致性问题的充分必要条件是相互作用的有向图存在一个生成树。关于多智能体之间的竞争关系，S.Ermon等人[3]提及的对于自治网络在工程应用中的事实估计的情况，这种关系可以用符号图表示，即图中边的权重可以是负的，其中正权表示智能体间的合作关系，负权表示智能体间的竞争关系。关于正负混合权重的情形，C.Altanfini在文献[4]中研究了关于连通符号图(或强连通符号图)的二分一致性问题，并证明了在结构平衡的符号(有向)图下，基础一致性协议能够解决二分一致性问题。之后Zhang等[5]研究了系统达到二分一致性的条件，讨论了二分一致性和一般一致性之间的等价关系，扩展了基于黎卡提方程的协同跟踪控制器以解决二分一致性问题。

上述关于二分一致性的结论都是以节点动态来描述，但是在现实生活中，有很多物体，例如道路，电线，甚至个体间的相互关系和作用的实体等并不能简单地用通常的节点动态来描述，而是用边动态来描述。拿交通网络来举例，用边动态来描述更合理准确，具体而言，对于单行道，用有向边来表示，对于双行道，用无向边或双向边表示，我们期望交通网络中不存在一些道路拥堵而一些道路冷清的情况，使所有道路的交通状况能达成一致，即道路交通网达成边动态一致性。关于边动态的研究目前很少，Wang等人[6]研究了一阶多智能体系统的边动态一致性问题，在有向图下建立了边动态一致性协议，利用了线图这个工具，解决边动态问题，并且证实了在强连通有向图下，多智能体系统能实现边动态一致性。

此外，实际问题中智能体之间的信息传递往往会存在通讯时滞，导致系统的动态特性变差甚至导致系统无法实现稳定性，因而针对含有通讯时滞的多智能体系统的问题研究也受到了广泛关注。2004年，Saber等人[7]研究了一阶动态系统在均匀固定交流时滞下有向网络的平均一致性问题。之后，Du在[8]中研究了一阶多智能体系统在具有正负混合权及通讯时滞的无向拓扑下的二分一致性问题，构造了含不均匀时滞的一致性协议，给出了时滞多智能体系统实现二分一致性的结论。Li等人[9]研究了无向拓扑下一类含有固定时滞的二阶多智能体系统的二分一致性问题，其中对于含有交流时滞情形下的一致性及二分一致性问题的分析，借助了一类等价变换，将系统的一致性问题等价为稳定性问题。2018年，Tian在[10]中研究了二阶时滞系统正负混合加权的系统二分一致性问题，利用矩阵论的方法对二阶系统进行降阶处理，简化分析。上述关于符号图下系统的二分一致性都是在结构平衡这个条件下得到，2017年Jiang在[11]中对非结构平衡条件下系统的二分一致性进行了研究，并设计了不需要整个拓扑图信息的完全分布式控制器。目前对时滞系统的稳定性分析主要有两类方法，一类是频域方法，如[12]、[13]，主要研究系统传递函数，一类是时域方法，如[14]、[15]，主要研究系统状态方程。对于含不均匀时滞的多智能体系统，通常采用时域法利用Lyapunov稳定性理论进行处理。其中[16]详细说明了Matlab中的LMI(线性矩阵不等式)工具箱，据此可以解决由Lyapunov方程产生的线性矩阵不等式的求解问题。

在上述工作的基础上，本文基于边动态重新设计了一阶和二阶系统模型的二分一致性协议，使系统在实现二分一致性时系统各边状态趋于模相等。在考虑边动态时，利用线图这一工具，将系统模型的边动态转化为节点动态，之后在研究二分一致性问题时利用规范变换将其等价为普通的一致性问题，并通过矩阵变换将多智能体系统的一致性问题等价为稳定性问题，利用边与节点之间的转化关系分别得到一阶、二阶系统实现边动态二分一致性的充分条件。与[4]不同，由于在实际多智能体网络中，信息在传递过程中存在着不同的损耗和时滞，因此，本文在上述边动态二分一致性的基础上，进一步在协议中加入了不均匀的通讯时滞。在解决含时滞系统的二分一致性问题时，在上述稳定性问题的基础上，利用Lyapunov渐近稳定性理论，构造含时滞信息的Lyapunov-Krasovskii泛涵，并对泛函进行求导，在求解Lyapunov-Krasovskii泛涵时，本文利用Matlab中的LMI工具箱对其进行处理，利用gevp求解器解出满足系统稳定时的最大通讯时滞，进一步得到含时滞多智能体系统实现边动态二分一致性的充分条件。

本文的结构如下安排：第2节介绍了线图、结构平衡等相关图论知识以及边动态下的一阶(二阶)系统的二分一致性协议；第3节给出了关于一阶(二阶)系统关于二分一致性的结论及证明；第4节针对上章结论分别进行了仿真，并给出了仿真结果；第5节总结了本文所做工作。

1 预备知识

1.1 图论

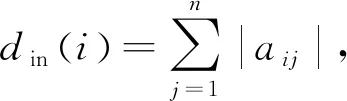
1.1.1 结构平衡

定义1结构平衡：如果强连通的有向图的所有的环都是正的，那么它是结构平衡的。换一种说法，如果强连通的有向图的节点都可以被分为V1,V2，其中V1∪V2=V,V1∩V2=φ且aij≥0,∀i,j∈Vp,(p∈{1,2}),aij≤0,∀i∈Vp,j∈Vq,(p,q∈(1,2),p≠q)，则其是结构平衡的。否则，称为结构不平衡。

引理1[4]当且仅当以下等式成立，对边符号对称的强连通有符号的有向图G(A)结构平衡：

1)G(A)的所有有向环均为正；

2)∃D使得DAD所有的元素都是正的；

3)0是L的特征值。

推论1当且仅当0是拉普拉斯矩阵L的单特征值，也就是说rank(L)=n-1，对边符号对称的强连通的有符号有向图G(A)是结构平衡的。

1.1.2 线图

n个节点m条边的有向图G={V,E,A}，其线图L(G)定义为[6]：

1)L(G)中的节点(i,j)对应于G中的有向边(i,j)；

2)对于G的节点i，在线图L(G)中其入边(i,j)与其出边(k,i)相邻，其中i,j,k=1,2,…,n。

值得注意的是，我们在符号的有向图及其线图中有以下规则：

1)从原始图的负加权入边生成的线图中的边取负权重；

2)从原始图的正加权入边生成的线图中的边取正权重。

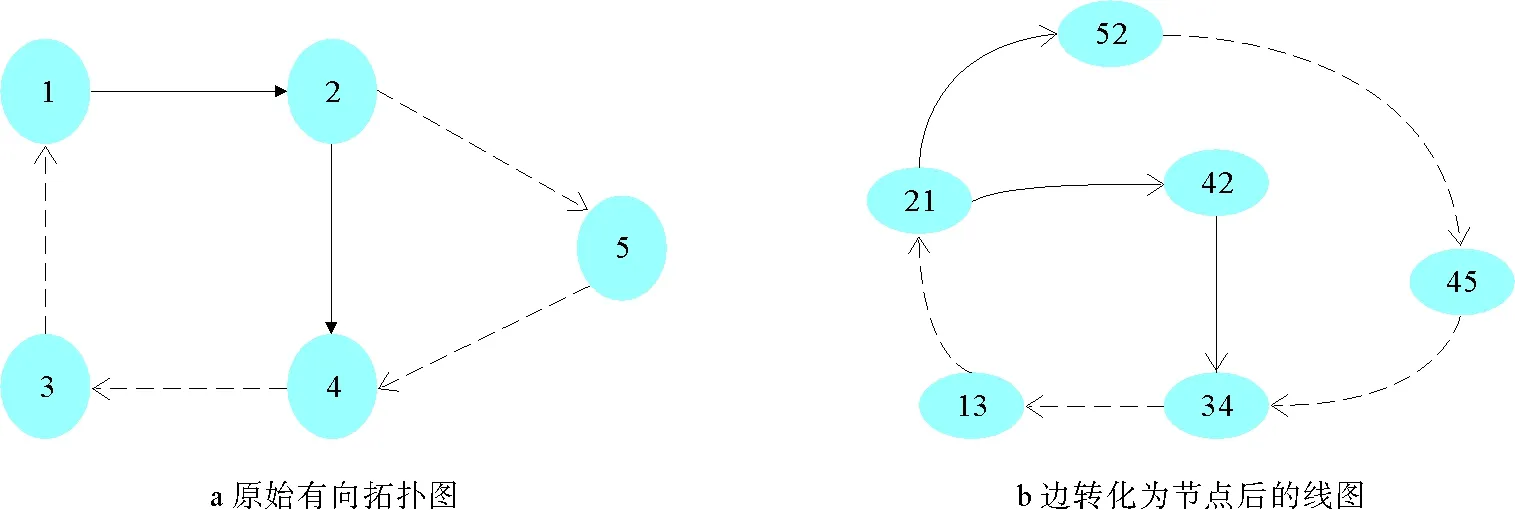
注：虚线表示负边，实线表示正边图1 原始有向拓扑图和边转化为节点后的线图

关于原始拓扑图及其线图有如下引理：

引理2[10]如果有向图G包含超过一个节点且是强连通的，则其线图L(G)也是强连通的。

引理3[10]当且仅当G是结构平衡的，对于强连通的对边符号对称有符号有向图G，其线图L(G)是结构平衡的。

1.2 一致性协议

假设多智能体系统有n个多智能体，这n个多智能之间有M个边，用边动态来表示多智能体之间的连接关系：

(1)

(2)

上述(1)为一阶系统模型，(2)为二阶系统模型，其中xij(t)∈R表示边ij的状态，vij(t)∈R表示边ij的速度，uij(t)∈R表示边ij的控制协议或输入。为了方便描述，下面的叙述中在不引起混淆的情况下省略时间变量t，例如uij(t)写成uij。

(3)

其中，c为任意常数，则称该系统可以实现边动态二分一致性。

对于系统(2)，其实现边动态二分一致性时，各边状态如下：

(4)

对于二分一致性问题(3)、(4)，在多智能体系统(1)、(2)不受通讯时滞影响的情况下，考虑其一致性控制协议分别为：

(5)

(6)

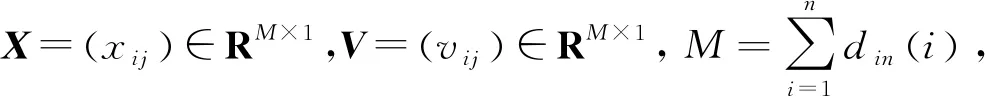
(7)

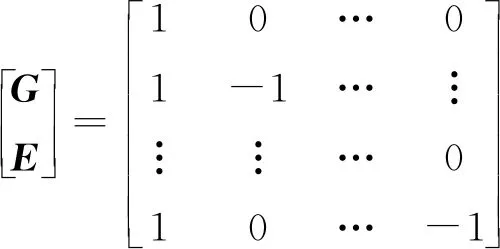
基于L′=[l′ij]M×M=C′-A′可知，将协议(5)、(6)分别用于系统(1)、(2)，可得：

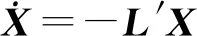
(8)

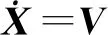
(9)

在实际应用中，各智能体间的信息传输往往不可避免地存在着通讯时滞。为了解决通讯时滞问题，我们在一致性协议(5)、(6)中分别加入不均匀通讯时滞得到如下协议：

(10)

(11)

其中,τij表示第i个智能体获得第j个智能体状态信息时存在的通讯时滞,对于边动态系统，由于研究对象是图的边，而时滞信息主要存在于边上，因此将原始拓扑图转化为线图之后，其线图的边并不存在时滞，时滞信息储存在线图的节点中，我们做出如下定义:

定义2线图中节点之间的时滞由发送信息的节点(即图1b的非箭头端节点)确定。

由于不同智能体之间的通讯距离不一定相同，设多智能体系统中不同的通讯时滞个数为m，其中m≤M,记第k个通讯时滞为τk,k∈{1,2,…,m}，并且令0<τ1<τ2<…<τm≤d，其中，d为通讯时滞上界。那么将协议(9)，(10)分别用于系统(1)，(2)可得如下模型：

(12)

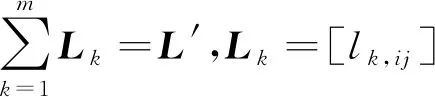
其中，N(k,i)={j|j≠i,τij=τk}。

2 主要结论

2.1 一阶无时滞系统的边动态二分一致性

首先，引入一类正交矩阵D，其定义为:D={diag(σ),σ=[σ1,σ2,…,σn],σi∈{-1,1}}其中，D满足DTD=DDT=I(单位阵)，并且D-1=D。

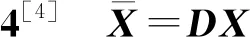
(13)

其中，常数c′满足|c′|=|c|。

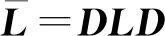
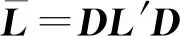
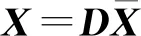
(14)

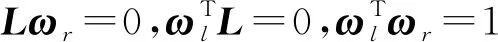
(15)

基于上述二分一致性条件(3)并根据引理4，容易看出一致性等价地表示为

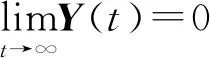
(16)

即多智能体系统的一致性问题可以转换成一个关于Y的稳定性问题。由(9)可得：

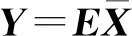
(17)

(18)

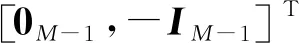
(19)

(20)

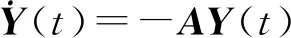
(21)

根据上述描述，可以得到以下结论。

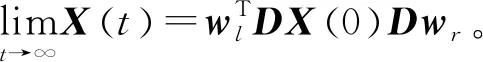
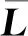
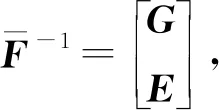
对H求导如下：

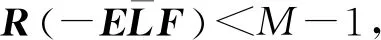
2.2 一阶含时滞系统的边动态二分一致性

引理7[17]设x,y为任意n维实向量，H为n×n维可逆对称矩阵，则下面的矩阵不等式成立：

2xTy≤xTH-1x+yTHy

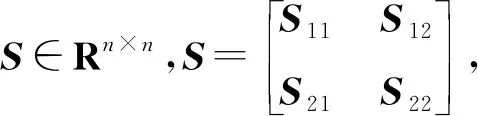
1)S<0；

对一阶多智能体系统存在通讯时滞的情形，类似于式(20)的建立，我们由式(11)可得：

(22)

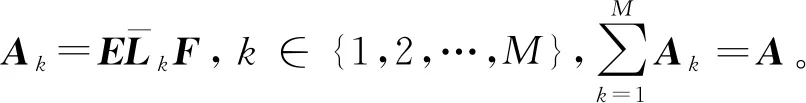
定理2对于一个有向强连通图G(A),如果G(A)是结构平衡的。假设存在m个固定时滞τk，当存在对称正定矩阵P,Qk,Wk∈R(M-1)×(M-1)，k∈{1,2,…,M}使下面式子成立：

(23)

(24)

那么，一阶含时滞多智能体系统能够实现边动态二分一致性。

证明：构造Lyapunov-Krasovskii泛函：

V(t)=V1(t)+V2(t)+V3(t)

其中：

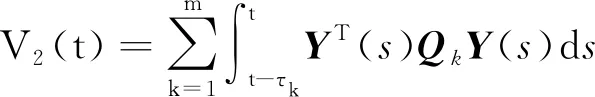
对V(t)求导可得：

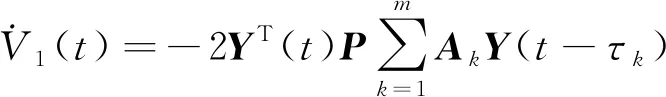
由Newton-Leibniz公式和引理8可知：

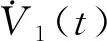
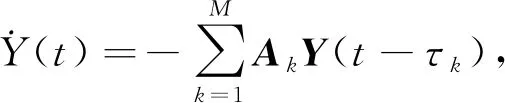
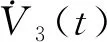
得到：

其中,

(25)

(26)

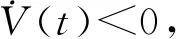
2.3 二阶无时滞系统的边动态二分一致性

如同一阶系统，二阶系统经规范变换之后模型如下：

(27)

其中,

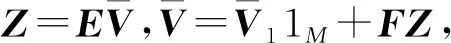
如一阶模型分析可得如下结果：

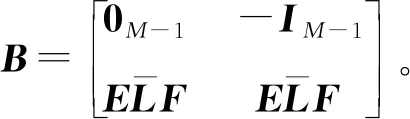
(28)

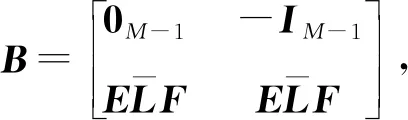
(29)

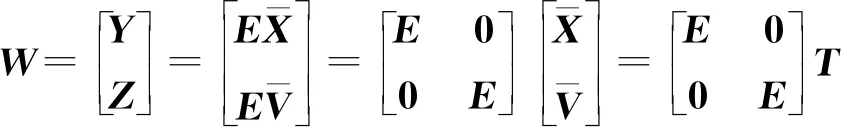
(30)

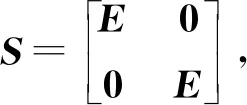
2.4 二阶含时滞系统的边动态二分一致性

将协议(10)代入到(28)中可得到如下系统模型：

(31)

类似一阶系统，将上述模型转换为式(20)的形式，则转换之后的系统模型如下：

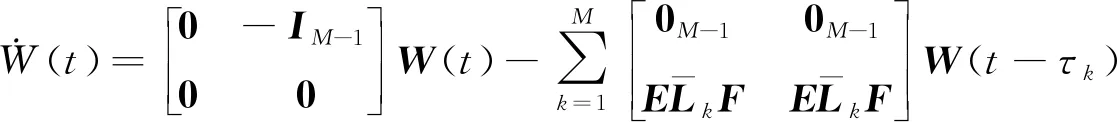
(32)

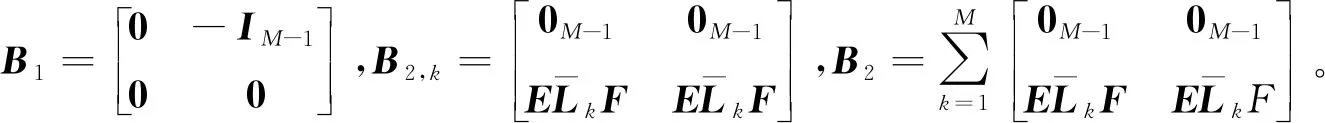
证明：

必要性：根据W的定义，显然必要性成立，即二阶系统实现二分一致性时降阶系统的每个解均趋于0。

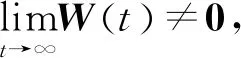
根据上述分析，可以将一致性的证明转化为对转换系统的渐近稳定性的证明。

定理4在协议(10)下，对于给定的最大通讯时滞d，如果存在正定对称矩阵P,Qk,Rk使下式成立：

(33)

那么系统(2)能实现边动态二分一致性。其中：

(34)

证明：同上述一阶系统，选取如下Lyapunov-Krasovskii泛函：

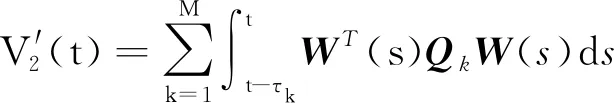
其中P,Qk,Rk定义如上文所述，分别求导后结果如下：

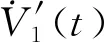
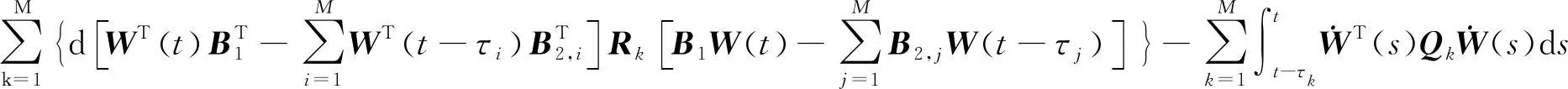
将上述泛函整理成矩阵形式：

(35)

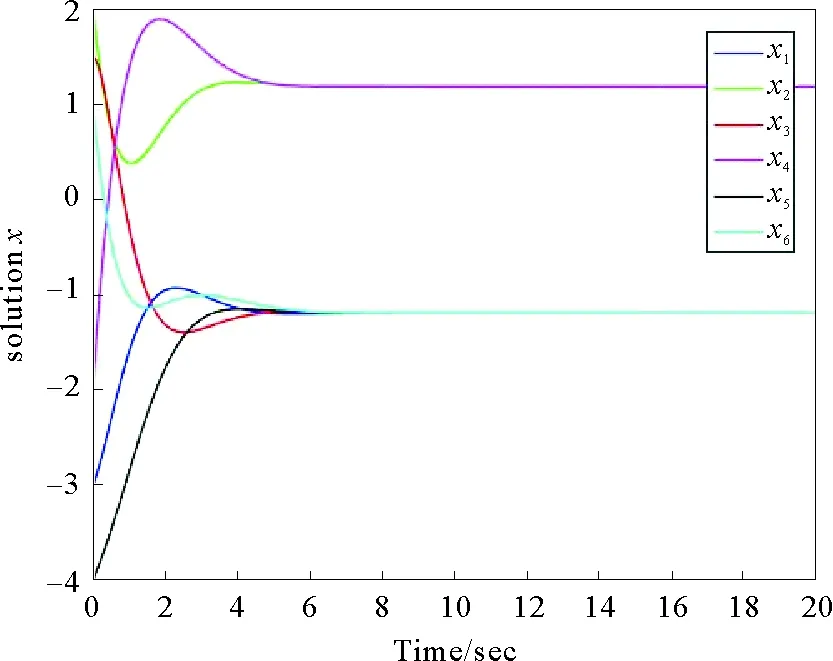
图2 无时滞情况下一阶系统的边动态二分一致性情况

3 仿真

3.1 无时滞多智能体系统的边动态二分一致性仿真

考虑由5个节点构成的多智能体系统，其有向拓扑连接如图1a，其中实线表示个体之间的合作关系，权重取+1，虚线表示的是个体之间的竞争关系，相应的权重取-1。将其转化为线图之后，其对应的边动态有向拓扑图如图1b所示，可以看出原始拓扑图和线图均为强连通，并且都是结构平衡的。考虑一阶系统模型(1)，取各边初始状态为：x21=-3,x13=2,x34=1.5,x45=-2,x52=-4,x42=1。其仿真结果如图2所示，可以看出当系统中不存在时滞时，对边符号对称的一阶强连通有向多智能体系统能实现边动态二分一致性。进一步考虑二阶系统模型(2)，取各边初始状态为：x21=-3,x13=2,x34=1.5,x45=-2,x52=-4,x42=1，v21=2,v13=-1,v34=-3,v45=7,v52=6,v42=3。其仿真结果如图3所示，可以看出二阶强连通有向多智能体系统也可实现边动态二分一致性。

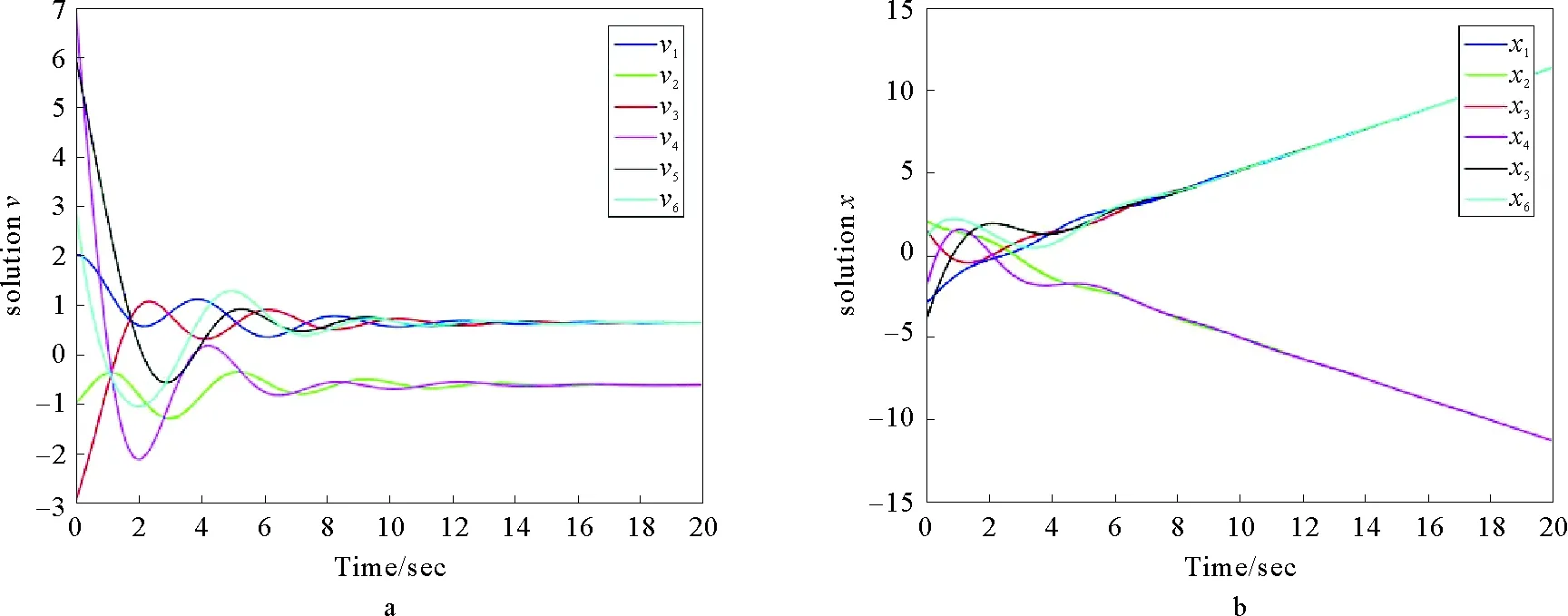
图3 无时滞情形下二阶系统的边动态二分一致性仿真

3.2 含时滞多智能体系统的边动态二分一致性仿真

考虑将时滞加到多智能体系统中，对系统(1)进行分析,利用控制协议(9),同样选取图1a为系统的拓扑结构，取系统的6个边的初始状态为：x21=-3,x13=2,x34=1.5,x45=-2,x52=-4,x42=1，根据式(22)和式(23)可求得通讯时滞上界d=0.555 3，在通讯时滞上界的范围内，我们选取τ21=0.455 3,τ13=0.355 3,τ34=0.255 3,τ45=0.155 3,τ52=0.055 3,τ42=0.555 3，作为对照，另选取一组时滞使其超过通讯时滞上界τ21=0.855 3,τ13=0.553,τ34=0.7,τ45=0.6,τ52=0.055 3,τ42=0.555 3，仿真结果如图4所示，图4a表明在不超过通讯时滞上界的前提下，对边符号对称的强连通有向图加入时滞后依然可以实现边动态二分一致性，图3b表面当边缘时滞超过了通讯时滞上界后，系统无法再实现边动态二分一致性。进一步考虑二阶系统模型(2),采用式(10)表示的控制协议，根据式(30)可求得通讯时滞上限d=0.146 0,在通讯时滞上界的范围内，我们选取τ21=0.146 0,τ13=0.106 0,τ34=0.046 0,τ45=0.086 0,τ52=0.076 0,τ42=0.026 0，仿真结果如图5所示。

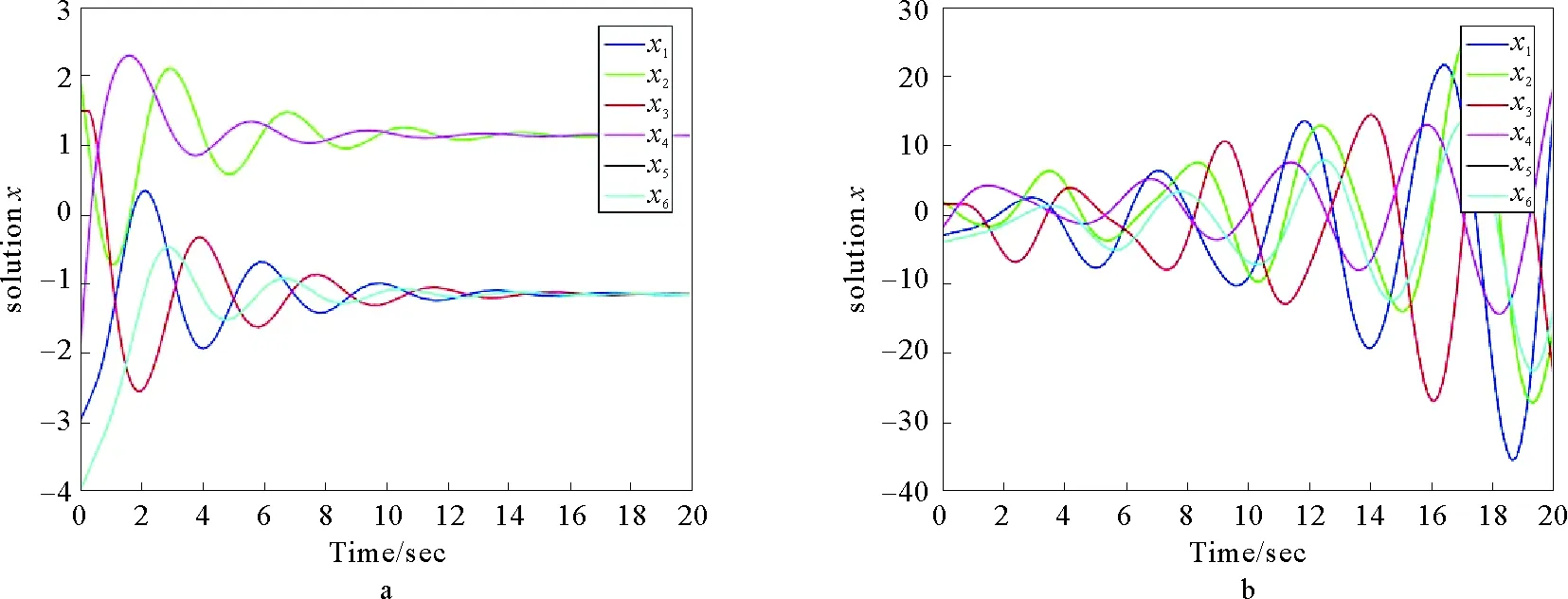
图4 含时滞一阶系统的边动态二分一致性仿真

图5 含时滞二阶系统的边动态二分一致性仿真

4 总结

本文基于边动态分别设计了无时滞和含时滞多智能体系统的二分一致性协议，研究了对边符号对称的强连通有向图下的多智能体系统的边动态二分一致性问题。分别针对一阶和二阶系统给出证明，得到系统在无时滞和含时滞情况下实现边动态二分一致性的充分条件，并利用Matlab进行数值仿真验证方法的合理性。最后本文的结论仍在结构平衡这个限制条件下得到，未来的研究重点是打破这个限制条件。