环形桁架天线展开动力学分析

任伟峰 何柏岩 聂 锐

天津大学机构理论与装备设计教育部重点实验室，天津，300354

0 引言

空间大型可展开天线是卫星上将电磁波导能按要求转换成空间电磁波能或将空间电磁波能按要求转换成电磁波导能的转换设备，在卫星通信、深空探测、地球监测、军事侦察和科学研究等方面均有重要作用。航天技术和相关应用的快速发展对空间大型卫星天线提出了更高的要求。环形桁架可展开天线因诸多优势，如可实现口径较大(6～150 m)、质量小、折展比较高、刚度较好及质量不随口径增大而成倍增大等特点，成为目前研究最为广泛的一种星载天线[1-3]。

环形桁架可展开天线也称AstroMesh天线，于2000年在Thuraya卫星上首次应用[4]。由于体积和质量的限制，天线在发射阶段必须完全折叠并放置于运载火箭整流罩中。卫星入轨后，天线在微重力条件下缓慢展开，最终至完全展开并要求索网达到预定形面精度[5]，天线服役期间，必须保持足够刚度和稳定性，以满足工作需求。

星载天线展开不满足工作要求主要有以下两方面原因：天线未能在太空微重力环境下实现展开；尽管完全展开但展开过程不稳定，致使索网未达到预定形面精度。这两种情况均会导致天线无法正常工作，所以必须对天线的展开过程进行相关动力学仿真计算以及性能预测。

动力学模型作为动力学分析的基础，模型构建越精确，动力学分析结果越准确可靠。文献[6-7]基于Lagrange方程，利用集中质量法建立了天线动力学模型，并进行了相关分析。但集中质量法忽略了所有杆件的转动动能，建立的动力学模型与天线实际情况并不完全相符，且索网模型构建误差较大。文献[8]考虑杆件平动和转动动能，基于Lagrange方程建立了动力学模型，计及索网弹性势能进行了逆动力学分析，但未计及斜杆随展开角变化后引起的动能变化。

环形桁架天线的展开过程通常是先由扭簧驱动展开至某角度，以避开初始时刻的死点位置，再由电机拉动斜杆中的绳索继续驱动从而实现完全展开。一些文献仅对电机驱动部分进行了相关研究[9-10]，而未考虑扭簧驱动的部分，所以需要深入研究扭簧驱动参数的影响。

文献[11-12]对环形天线展开的逆动力学进行了研究，给定预设展开角的轨迹，得到斜杆中驱动绳索的驱动力，以确定天线展开角按照何种展开轨迹使得天线能够平稳顺利地展开且冲击较小。但天线的展开通常是由扭簧与电机联合驱动的，其中电机间接拉动斜杆中的驱动绳索使天线展开，故必须按照实际情况对展开过程进行正动力学分析，给定系统驱动，分析天线展开的动力学行为。通过扭簧和电机的联合驱动来实现逆动力学规划的较完美的展开角轨迹，也必须验证其操作在现实中是否具有可行性。因此，对环形天线的完整展开过程进行正动力学分析是非常有必要的。

本文基于Lagrange动力学方程，考虑系统动能、索网弹性势能、重力势能以及系统耗散能等，构建了环形桁架天线完整的展开动力学模型，分析了随天线展开角变化而变化的斜杆动能。电机驱动天线展开阶段的实际情况是由桁架斜杆中绳索拉动间接实现的，故对电机驱动的研究可转变为对斜杆中绳索驱动力的研究。综合扭簧驱动和电机驱动，对环形天线整个展开过程进行了正动力学分析，并研究了扭簧与绳索驱动力的相关参数对天线展开过程的影响。

1 环形桁架运动学分析

环形桁架天线主要由环形桁架、前后索网、张力阵和金属反射网(未画出)等部分组成(图1)，其展开原理是利用平行四边形对角可伸缩的特点，实现环形桁架的折叠与展开[13]。

图1 环形桁架天线模型Fig.1 Model of hoop truss antenna

环形桁架(图2)包含许多完全一致的平行四边形单元，每个平行四边形单元包含竖杆、横杆、斜杆、三向铰链及五向铰链等。设定每个单元中所有杆件的质量都沿纵向均匀分布，铰链质量分别集中于各节点上，五杆相交的节点(如D1点)代表五向铰链，三杆相交的节点(如A1点)代表三向铰链，且各杆件和铰链均视为刚体。假设桁架共由n(n≥ 4且为偶数)个平行四边形单元构成，所有单元分别从1至n依次编号。A1B1代表固定的竖杆，(x1,y1,z1)是第1个平行四边形单元的局部坐标系，也是系统全局坐标系。(x2,y2,z2)是第2个单元的局部坐标系，其他单元以此类推，坐标系原点均固定在平行四边形单元节点上。在天线展开过程中，同一平行四边形单元中的铰链和杆件始终保持在同一平面内。

图2 环形桁架坐标系设定Fig.2 Coordinate system setting of hoop truss

平行四边形单元的展开是通过斜杆伸展实现的。图3是两相邻桁架单元的简化示意图，Aj、Bj、Cj和Dj分别代表第j个单元的各节点，第j个单元的节点Cj和Dj分别与第j+1个单元的Bj+1和Aj+1重合。天线展开角φ是平行四边形单元中横杆与竖杆的夹角，其展开范围为0～π/2。φ1是竖杆和斜杆间的夹角。θ是两相邻桁架单元的夹角，其值取决于环形桁架的单元数目(θ=2π/n)。

第j个单元上任意点P在局部坐标系(xj,yj,zj)中的位置矢量r(j)可通过坐标变换，在另一坐标系(xi,yi,zi)中表示为

r(i)=T(ij)r(j)

(1)

(2)

式中，T(ij)为转换矩阵；R2为横杆长度；j>i，i≥1，j≥2。

图3 两相邻桁架单元Fig.3 Two adjacent units of truss

任意点P在另一局部坐标系(xi,yi,zi)中的速度变换方程为

(3)

各单元节点Aj和Bj在局部坐标系(xj,yj,zj)中的位置矢量分别为

(4)

式中，R1为竖杆长度。

(5)

其中，式(5)等号右边矩阵中的3个元素分别为节点在全局坐标系中X、Y、Z三个坐标轴的速度分量。

节点Cj和Dj的速度分别等于节点Bj+1和Aj+1的速度，即

(6)

各竖杆AjBj的质心速度

(7)

环形桁架在展开过程中，各竖杆AjBj只有平动运动，故角速度为0。各横杆AjDj的质心速度和角速度分别为

(8)

(9)

各横杆BjCj的速度及角速度可分别用上述方法得出。桁架的各平行四边形单元斜杆中驱动绳索长度

(10)

对于包含粗斜杆和细斜杆的斜杆整体，可利用质心方程及比例关系得到整个斜杆的质心速度，从而得到随展开角φ变化的整体斜杆动能。如图3所示，第j个单元中的粗、细斜杆在轴xj上的坐标分别为

(11)

j=1,3,…,n-1

(12)

j=2,4,…,n

(13)

式中，R3、R4分别为粗细斜杆的长度。

斜杆质心在轴xj上的坐标为

(14)

式中，m3、m4分别为粗、细斜杆的质量。

由上述计算公式可以求得桁架中各斜杆的质心速度

(15)

和各斜杆的角速度

(16)

2 系统动力学建模

2.1 动力学方程

将环形天线的展开角φ作为系统的广义坐标，基于Lagrange第二类动力学方程，考虑系统动能、索网弹性势能、重力势能及系统耗散能等，构建系统动力学模型：

(17)

式中，T为系统动能；Φ为系统耗散能；V为重力势能；E为索网弹性势能；Qφ为广义力矩。

2.2 系统动能

天线的索网(前后索网、张力阵和金属反射网)均为轻质材料，且在太空微重力条件下缓慢展开，可忽略索网质量[7]和动能影响，故仅考虑所有杆件及铰链的动能。针对展开初期因扭簧驱动致使天线结构产生振动而导致索网可能产生较大动能的问题，因目前尚未有精确模型可描述天线完整展开过程索网的能量变化，故本文忽略了此阶段的索网动能。

依据运动学分析，可得桁架所有杆件的动能

(18)

Jl=m2R2/3

其中，m1、m2分别是竖杆和横杆的质量；Jl是横杆的转动惯量；Jj是斜杆的转动惯量，可由下式求得：

(19)

所有铰链的动能

(20)

式中，mt、mf分别为三向铰链和五向铰链的质量。

由此得到系统总动能

T=Tr+Th

(21)

2.3 索网弹性势能

金属反射网附着于前索网上，在天线展开过程中，由于索网和金属反射网的刚度大小不一，虽然能实现同时展开和折叠，但因各自能量变化过于复杂，故为简化计算，分析时只考虑前后索网和张力阵，而未考虑金属反射网的能量变化，由此也忽略了金属反射网的弹性势能[14-15]。因忽略了索网动能，故只计算前后索网和张力阵的弹性势能。针对索网弹性势能，采用文献[16]的研究理论，可有效模拟展开过程中索网的弹性势能，简述如下。

将索网离散为许多索段单元以建立其等效模型，且每个索段单元均等效为线性弹簧。设定索网有m个索段单元，n′个节点(n′f个自由节点和n′b个边界节点)，每个索段单元可由索段相应两端的节点确定，故任意索段单元i′在时刻t的坐标差矢量

Ci′=(Δxi′(t),Δyi′(t),Δzi′(t))

(22)

因忽略索网质量，故自由节点在展开过程中无任何外力作用。各自由节点在t时刻的平衡方程为

(23)

式中，Tf为索网自由节点的拓扑矩阵；Qk(t)为索段力与长度之比的矩阵；Δx(t)、Δy(t)、Δz(t)分别为所有索段单元的坐标差矢量。

将通过找形法获得的天线完全展开状态时的索网自由节点坐标作为初始值，利用信任域算法对非线性方程求解。从天线完全展开至折叠状态的逆过程进行分析，每一个时间步的自由节点坐标均可由式(23)求得。得到索网的弹性势能

(24)

式中，ki′(t) 为任意索段单元i′在t时刻的刚度系数；li′为索段单元i′的原始长度。

索网随桁架的展开而伸展，故采用多项式拟合法可得到索网弹性势能E与展开角φ的函数关系：

E=f(φ)

(25)

2.4 重力势能

天线展开过程中，环形桁架的重力势能

(26)

式中，g为重力加速度。

2.5 系统耗散能

环形桁架天线的展开过程较为缓慢，此处可将铰链阻尼看作黏性阻尼，并与展开角速度成正比。根据Rayleigh耗散公式[17]，系统耗散能

(27)

式中，ξ为阻尼系数。

2.6 系统驱动

天线展开初始阶段由五向铰链中的扭簧单独驱动，扭簧个数与平行四边形单元数相同。扭簧的角度变化与天线展开角度变化一致，即天线展开角φ转动多少度，所有扭簧也转动相同角度。扭簧的扭矩M为Lagrange方程中的广义力矩，即

M=nk(φe-φ)/2

(28)

式中，k为扭簧刚度系数；φe为扭簧零势能位置。

展开第二阶段，天线由电机拉动斜杆中的驱动绳索实现展开，故可将电机驱动的研究转变为对绳索驱动力的研究。将斜杆中绳索驱动力视作广义坐标，并建立广义力矩Qφ与驱动绳索的广义拉力QL的关系：

(29)

将上述计算结果分别代入式(17)，即可得到环形桁架天线完整的展开动力学模型。

3 算例分析

3.1 参数确定

选取18个平行四边形单元组成的环形桁架天线为研究对象，各参数见表1。天线在太空微重力环境下缓慢展开，故可忽略系统重力势能影响[18]。

表1 18单元环形天线参数

对各节点进行编号，天线前后索网的拓扑构型、各索段原始长度详见文献[16]。展开过程中索网弹性势能可通过前述方法得到，使用四阶多项式拟合得到索网弹性势能E与展开角φ的函数关系[8]：

(30)

式(30)可近似作为天线在实际展开过程中随φ变化的索网弹性势能。

3.2 动力学模型对比

将本文分析的环形天线动力学模型与其他文献中另2种动力学模型进行正动力学对比分析。模型1采用集中质量法[6]；模型2考虑了杆件平动和转动动能，但未考虑随展开角φ变化的斜杆动能[8]；模型3(本文构建的动力学模型)分析了所有杆件平动和转动动能，且考虑了随展开角φ变化的斜杆动能。

假设给定天线系统一个恒定驱动力200 N，分别对3种动力学模型进行对比分析。设定天线的初始展开角位移为π/180，以避开死点位置，展开终了时刻的角位移为π/2。角位移和局部角位移对比如图4和图5所示。可看出，模型2和模型3的仿真结果较为接近，比模型1的精度高。因集中质量法忽略了杆件的转动动能，且对斜杆的分析不完善，故模型误差较大。模型2忽略了随展开角φ变化的斜杆动能。模型3基于模型2，考虑了展开过程中随展开角φ变化的所有斜杆动能，但因天线展开较为缓慢，斜杆动能变化较小，故与模型2的结果相差不大，但对于实际中极为精密且要求较高的星载天线，本文构建的动力学模型仍具有非常重要的借鉴意义。

图4 三种模型的角位移对比Fig.4 Comparison of angular displacement of three models

图5 三种模型的局部角位移对比Fig.5 Comparison of local angular displacement of three models

3.3 不同扭簧零势能位置对比

天线展开初始阶段仅由五向铰链中的扭簧单独驱动，然后与电机一起驱动天线展开。若使扭簧在展开前期做正功，后期做负功，则可减小展开最后时刻的系统动能和冲击，故研究扭簧驱动部分对天线展开过程的分析是非常重要的。在绳索驱动力相同的情况下，研究扭簧不同的零势能位置φe对天线完整展开过程的影响。确定3种扭簧的零势能位置进行分析，天线展开终了位置：φe=π/2，扭簧预扭转角为π/2；索网开始张紧位置：φe=1.415 rad，扭簧预扭转角为0.155 8 rad；索网未开始张紧位置：φe=π/4，扭簧预扭转角为π/4。天线展开角φ的范围为0～π/2。

天线展开第二阶段为电机拉动斜杆中绳索实现展开，故对电机驱动的研究可转变为对绳索驱动力的研究，设定展开角φ=π/6时电机开始驱动天线展开。给定斜杆中绳索驱动力QL的表达式：

(31)

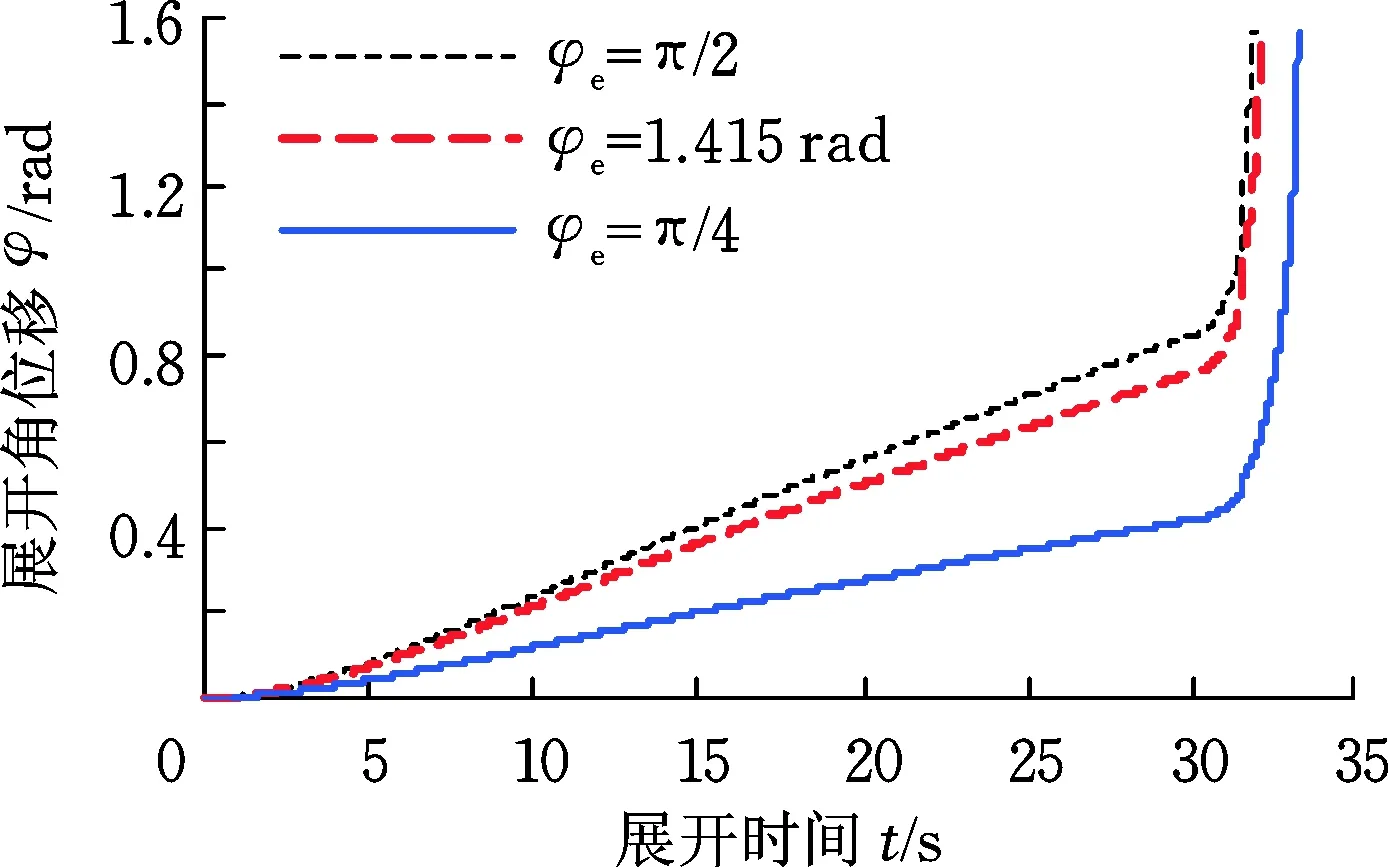
图6 不同零势能位置的角位移对比Fig.6 Comparison of angular displacement of different φe

系统展开角位移和角速度的结果如图6和图7所示。分析可知：①经规划的扭簧驱动和电机驱动可使天线完全展开；②其他参数不变，扭簧的零势能位置φe值越小，扭簧初始扭矩越小，且因在φe<φ<π/2阶段做负功，故展开所需时间越长；③φe越小，初始阶段角速度越小，但因展开时间较长，后期绳索驱动力的累积效应越来越大，故最后的角速度值也越大；④局部角速度对比如图8所示，可知角速度在最后阶段都有一个减小或增速减缓过程，此阶段索网开始张紧，且张力逐渐增大到最大值；⑤φe值越小，最后的角速度值则越大，故展开终了时刻系统动能也越大，易使天线产生冲击。

图7 不同零势能位置的角速度对比Fig.7 Comparison of angular velocity of different φe

图8 不同零势能位置的局部角速度对比Fig.8 Comparison of local angular velocity of different φe

若想使扭簧在展开前期做正功，后期做负功，以减小展开最后时刻的系统动能和冲击，仍需进一步研究扭簧与绳索驱动力参数的相互配合关系。

3.4 不同绳索驱动力对比

天线展开的第二阶段主要由绳索驱动力驱动，同时有扭簧参与，故需分析扭簧参数不变情况下绳索驱动力变化对天线展开过程的影响。设定扭簧单独驱动天线展开至φ=π/6，之后再附加绳索驱动力共同驱动展开，扭簧零势能位置为φe=π/2。另两种对比驱动力QL1和QL2分别为

(32)

(33)

三种驱动力分析得出的系统角位移和角速度如图9和图10所示。分析可知：①驱动力越大，天线展开所需时间越短，且展开终了时刻的角速度越大，所以展开最后时刻系统动能也越大；②若驱动力在索网开始张紧后的变化不足以驱动天线进一步展开，则天线角位移有一段停滞，会使系统产生振荡，可能致使索网由于展开惯性而发生缠绕现象，需等到绳索驱动力增大到能够继续驱动天线展开时再次展开；③驱动力的选择不能过大或过小。力较大时虽展开时间较短，但展开终了时系统动能过大，易对系统产生冲击。力较小时虽展开时间越长，但可能会出现持续振荡的阶段，均不利于天线平稳顺利展开。

图9 三种驱动力下角位移对比Fig.9 Comparison of angular displacement under three driving forces

图10 三种驱动力下角速度对比Fig.10 Comparison of angular velocity under three driving forces

4 结论

(1)本文建立了环形桁架天线完整的展开动力学模型，其中考虑了随展开角φ变化的斜杆动能和索网弹性势能，并与其他文献的动力学模型进行对比分析，验证了该动力学模型的有效性。

(2)依据构建的环形桁架天线动力学模型，结合扭簧驱动和电机驱动，并将研究电机驱动转变为对绳索驱动力的研究，对天线完整展开过程进行了正动力学分析。结果证明经规划的扭簧驱动和电机驱动可使得天线完全展开。

(3)设绳索驱动力不变，分析扭簧驱动对天线展开过程的影响。若想使扭簧在展开前期做正功，后期做负功，以减小展开终了的系统动能，通过单独改变扭簧的零势能位置较难时实现，故需进行多参数分析以实现该目的。

(4)对绳索驱动力进行了深入分析。驱动力较大，虽天线展开时间较短，但是展开后期系统动能越大，容易产生冲击。驱动力较小，可能不足以持续驱动天线展开运动，展开过程中会产生振荡阶段，可能致使前后索网由于展开惯性原因而发生缠绕现象，对天线展开不利。

下步工作将具体研究如何优化扭簧和绳索驱动力的参数，使天线在展开过程中仅有较小冲击，以实现平稳顺利展开。