排爆机器人机械臂定位精度误差自动补偿方法研究

丁 燕，刘 鑫2，黄炜亮

(1.连云港工贸高等职业技术学校 机械工程系，江苏 连云港 222000；2.中南大学 商学院，湖南 长沙 410083)

0 引言

国际上的恐怖分子所进行的恐怖袭击活动，爆炸袭击是惯用的手段之一，在进行排除爆破等工作，会出现很多突发情况，危险性极高。而排爆机器人不仅可以在危险的环境下对爆炸物进行检测、搜索、销毁、排除等工作，同时对人身安全进行保护，避免受到伤害[1]。

当排爆机器人进行现场操作的时候，由于一些爆炸物较小，对机器人机械臂的定位精度有极高的要求[2]。但是排爆机器人机械臂连杆与关节之间容易发生弹性变形，产生传动误差，导致最终机械臂的绝对定位精度有所降低，限制了机器人在进行排除爆炸物时无法达到高精确、高灵活的工作，造成严重的后果[3]。

通过对排爆机器人机械臂的误差进行分析可知，误差的来源是由机械臂的几何构造所引起的，这些误差无法采用闭环控制方式来减少，再受到成本以及加工方式的影响，单纯对加工精度的提高以及装配时的调整来减少或者去掉这些误差是不可能的，同样，经济条件也是一种负担。因此采用机器人机械臂误差补偿方法，提高执行端的定位误差[4]。

对排爆机器人的机械臂进行误差补偿时候，常用于两种方法：一是预测误差法，在进行设计与工作中尽可能地减少由设计、加工、装配时候带来的误差[5]；二是运动学标定法，根据合理有效的方式来分辨出机械臂理论上运动学轨迹数值和实际上的运动学数值之间误差，再用数值之间的对比来修正机械臂的运动学数值达到补偿的目的[6]。这两种方法相互对比，运动学的定位法要比预测误差法的成本低以及补偿效果好。同时对机器人机械臂零件之间的磨损等一些原因进行补偿，是现在机器人误差补偿重要的手段[7]。

运动学主要有4个组成步骤：建模、测量、辨识跟补偿。最常用的两种方法：一是圆周法先求出实际机器人机械臂关节的位置，在用几何关系得出机器人的误差数据。二是回路方法，先构建一个机械臂的运动学误差模型，采用先进手段与模型的数值得出机械臂真实数值。两种方法进行对比，回路法效果更好，避免了人为因素影响。在实际应用中广泛地用于机器人的标定过程[8]。

1 排爆机器人定位误差模型的构建

通过对排爆机器人机械臂的运动学合理分析，给出排爆机器人转动关节连杆示意图，如图1所示。以机械臂的坐标矩阵构建一个运动学模型，也就是D-H模型，先在关节处构建一个坐标系，再根据坐标系之间的转换及分析，得出机器人执行端的位置和姿态[9]。

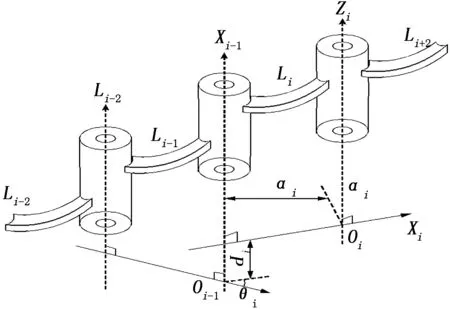
图1 转动关节连杆示意图

在两个关节之间的坐标矩阵如下：

i-1Ti=Rot(X,αi)Rot(Z,θi)Trans(Z,di) =

式中,i-1Ti为i的坐标系是对于i-1坐标系的转换矩阵；θi为排爆机器人机械臂的Xi-1跟Xi围绕Zi-1的夹角；di为机械臂关节Xi-1和Xi沿着Zi-1轴平移的长度；αi为机械臂Zi -1和Zi围绕Xi轴旋转的角度，αi为Zi -1与Zi是沿着Xi轴平移的长度。

di，ai，αi，θi是模型构造的参数，代表机械臂的关节以及连杆之间的关系。

机器人的机械臂关节沿着一定的轴线进行平行时，运动学模型就会产生奇怪的现象，这影响参数分辨的稳定性，所以在两个关节点的轴线平行运动时加一个围绕Y的轴线运动的数值β。在机械臂执行端坐标系位置上，根据关节之间的叠加变换计算出机械臂执行端位姿如下：

(2)

式中,n，o，a代表机械臂的执行端姿态的向量；p表示机械臂的执行端位置的向量。

因为机械臂连杆参数误差，所以理论上执行端位姿与其实际位姿存在一定的误差，用Δp=pr-pn来表示。pr是机械臂执行端实际的位姿矩阵，pn是理论上，机械臂执行端的位姿矩阵。机械臂的执行端位姿误差是由每一个关节之间相互转换积累而成的，因此要对关节的相邻坐标进行分析，获取关节的参数值误差与其执行端关节的函数关系。根据微分间的变换法，对相邻的机械臂关节进行齐次变换，可得：

(3)

同样，机械臂相邻关节平行坐标系的变换误差如下：

(4)

式中，Δθi表示机械臂连杆夹角偏差；Δαi表示机械臂连杆扭角误差；Δdi表示机械臂连杆距离偏差；Δai表示机械臂连杆长度偏差；TiΔi表示爆机器人机械臂相邻关节的变换误差；Δi表示机械臂关节坐标系相邻的变换矩阵；Δβi表示数值βi的偏差。

联立公式(2)和(4)，简化后可得：

(5)

式中,dxi，dyi，dzi表示机械臂关节i相当于关节i-1的X，Y，Z方向平行移动的偏差，将ei作为两个机械臂之间的关节转换位置与姿态的误差而构成的微分矢量，生成下列公式：

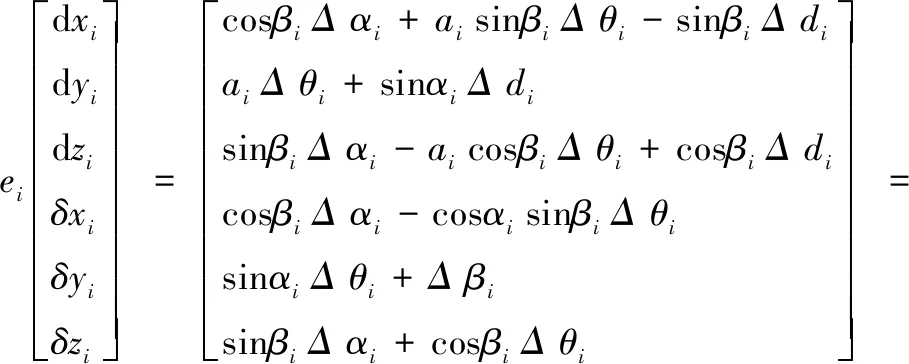
(6)

式中,Gi表示是机械臂误差系列的系数矩阵；Δxi表示是机械臂的连杆数值误差向量；δxi、δyi、δzi表示是机械臂的一个关节i对于关节i-1围绕着X、Y、Z轴线的旋转偏差。

根据公式(6)可得知，排爆机器人机械臂的连杆数值误差易造成机械臂近邻关节坐标齐次变换矩阵产生误差，而机械臂的执行端的绝对定位误差是由每个关节出现的一点小误差叠加而成的，所以将误差全部转移到机械臂的执行端坐标系上，即可得到机械臂执行端的位姿误差，根据微分转变原理，将机械臂的位置误差模型如下式：

(7)

式中,Ji表示机械臂的关节i坐标系到机械臂执行端坐标系的微分坐标矩阵，根据该矩阵能将机械臂关节处i的坐标误差转变到执行端上：

(8)

其中:n，o，a，p表示机械臂的关节坐标系i到执行端的坐标系经齐次变换后所得的位姿跟姿态向量；e表示在平面上机械臂执行端位姿误差向量；Je表示机械臂辨别雅克比矩阵；X表示机械臂的运动学误差参数[10-11]。

根据式(7)可得机械臂的运动学误差分辨模型，采用设备将机械臂误差的实际位姿测量出来，而理论上的位姿是根据机械臂的控制装置来获得，将实际位姿的测量结果输入到运动模型中，经过分析后即可得到排爆机器人机械臂的运动数值误差。通过对误差数值进行修正补偿，进一步提高排爆机器人定位精度[12-13]。

2 排爆机器人机械臂模型位置误差分析

2.1 重复性数值分析处理

在机械臂位置误差模型中进行分析求解时，模型中会有一些重复性参数，这些参数会降低误差辨识准确性，因此对构建的运动学模型，进行分析与判断，去掉重复的数值，以保证模型对重复数值进行有效的分析[14]。

对机械臂执行端误差模型(式7)根据下面简化方式，如下：

e=Je·X

(9)

假如机械臂模型中有重复的数值，证明分辨雅克比矩阵Je的列不是满秩，同时说明雅克比矩阵中的向量与线性有关或某列向量为零向量，因此需要对雅克比矩阵理解分析，找到与线性有关的列向量，且将列向量为零的向量进行消除，对除去列向量有关的误差性数值，即是重复参数。

2.2 列向量的相关性分析

根据公式(7)的微分转变矩阵Ji能得到机械臂关节i-1的坐标系下的误差ei-1。ei-1转变到机械臂关节i坐标下的变换矩阵：

(10)

机械臂关节坐标系i的微分误差是转移到自身坐标下的变换矩阵iJi：

(11)

式中,E表示单位矩阵。由公式(10)跟(11)能得到的iJi-1第3列跟第6列存在以下公式：

(12)

将公式(12)的两式都左乘6Ji微分的误差转变到机器人机械臂的执行端坐标系上，能得出机器人分辨雅克比矩阵的Je的第3列和第6列的线性相关，就是微分误差dzi与δzi用其他的微分误差表示。

根据公式(7)可得知，相邻的两个连杆其次变换误差都是由机器人机械臂的连杆几何参数误差决定的，所以要将公式(12)中的重复数值，dzi与δzi转变成连杆几何参数的冗余，将已知的理论连杆角度α代入公式(7)中，即可得到机械臂的几何参数冗余性，这有两种状况：平行关节时，重复参数dzi相对应的是Δdi，即Δdi就是重复参数；非平行关节时，重复数值δzi，相对应的是Δβi，Δβi视为冗余参数。

3 机械臂定位精度误差自动补偿方法

当辨识到排爆机器人机械臂的各个参数误差值后，对这些参数进行误差补偿，对Δa、Δα、Δd、Δθ、Δβ所对应的数值相加，构成新的参数，并在系统中对其进行修改。对指定的指令位姿参照新的数值进行逆运动学求解，得到关节转角θ=[θ1θ2…θ]T，在系统中将θ+Δθ的值相加作为θ值输出，从而控制所有轴的转动。

上述过程中构建了一个运动学模型，它的执行端末端变换矩阵是一个含有αi-1ai-1di与θi的矩阵，可在实际的应用中，它们存在一定的微小偏差。

假设，排爆机器人机械臂关节{i}的偏差值是Δαi-1、Δai-1、Δdi与Δθi，修正以后的数值是：

(13)

为了分析误差，对这些参数的敏感程度进行研究。在不同的位姿下，运动学参数误差对总位置误差的影响不同，假设机械臂所处的关节角度值为：

q=[0pi/4pi/6 -pi/3 2pi/3pi/6]

(14)

假设某一参数存在一个误差，剩余的参数不存在误差。根据一定的步长对所有关节进行改变，记录执行端位姿。最后，计算没有误差的执行端位姿与相应的有误差的执行端位姿的偏差，对其进行补偿。

4 实验结果分析

首先对排爆机器人机械臂几何参数误差进行求解。实验过程中，采用Mirosot机器人平台。机械臂执行器位置坐标利用激光跟踪仪进行测量。基于激光跟踪仪建立排爆机器人机械臂标准坐标系，测量不同位置处机械臂执行端实际位置坐标，将实际位置坐标和理论坐标进行对比，基于本文所构建的排爆机器人定位误差模型计算机械臂的几何参数误差。为了最大程度的提高标定的精度，使测量点分布于整个所需要工作的空间，选择了40个坐标点(20组相对点)来进行测量，根据上文中所建立的误差模型，识别的机械臂的几何参数误差如表1所示。

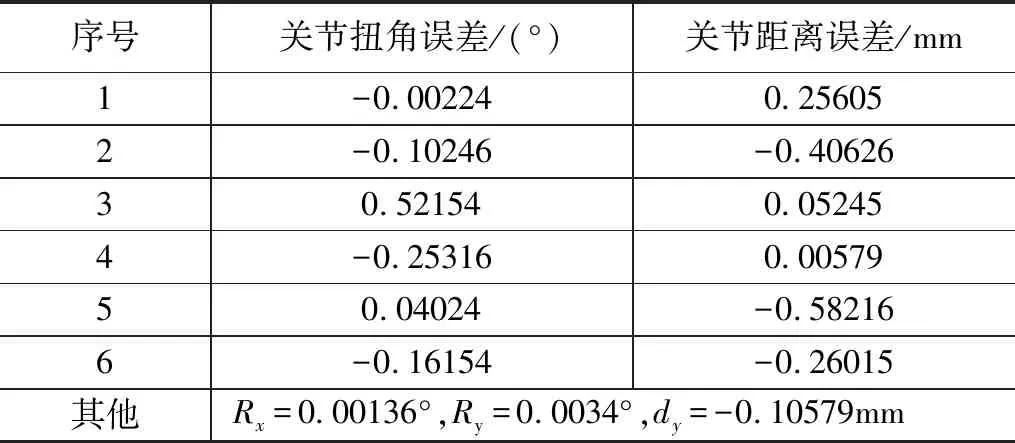
表1 机械臂的几何数值

接下来采用负重实验来求解排爆机器人的柔度误差。先将重量不同的物体施加排爆机器人关节之上，测量出负重前后关节坐标。利用公式(15)、(16)求出关节2与3的柔度系数，建立公式如下：

k2=5.91725×10-7N-1·m-1

(15)

k3=5.63819×10-6N-1·m-1

(16)

为了精确地计算出排爆机器人的柔性误差的补偿值，需要将关节的柔度系数代入误差模型之中，通过模型分析得到关节2与3转过不同角度所对应的偏差角度Δθg2与Δθg3，排爆机器人的偏转角度变化如图2所示。

图2 不同转角度关节偏转角的变化

由图2可知，排爆机器人机械臂机械臂负重实验所产生的柔度误差是随机械臂姿态改变而变化的，负重实验下关节转动所产生的角度误差较小，非常接近关节的4与5所能产生的转角误差，如表1所示。所以柔度误差对机械臂的绝对定位精度影响是可以无法忽略的。

排爆机器人机械臂关节的柔度误差进行准确的计算和有效补偿，能对机械臂的绝对定位精度有效提高。通过几何误差参数值与柔度误差参数数基础上，根据所构建的误差补偿方法，对测量出的40个位置点进行误差补偿，实验结果如图3所示。

图3 误差补偿前后定位绝对位置误差对比

通过图3可以看出，排爆机器人机械臂标定前的绝对定位误差相对于标定后的绝对定位误差数值要大了很多。由此可见，经误差补偿后，排爆机器人机械臂绝对定位精度均值提升了1.3 mm。

5 结束语

通过对排爆机器人机械臂的误差建模与实际位置误差进行分析，得出影响到执行端定位精度的主要影响因素包含几何误差与柔度误差。再通过几何误差标定后与运动学参数辨识结果，进行误差补偿。仿真实验分析证明，采用本文方法，几何结构参数辨识结果与实际位置之间差距很小。通过误差补偿后，执行端的定位精度相对传统的方法，误差较小，说明本文提高了排爆机器人机械臂的执行端绝对定位精度。