基于蒙特卡罗的复杂火工系统可靠性预计精度研究
付东晓,张国兴,张 蕊,李 芳,都振华,麻宏亮,平 川
基于蒙特卡罗的复杂火工系统可靠性预计精度研究
付东晓,张国兴,张 蕊,李 芳,都振华,麻宏亮,平 川
(陕西应用物理化学研究所 应用物理化学重点实验室,陕西 西安,710061)
针对蒙特卡罗方法进行复杂火工系统可靠性预计过程中存在误差的问题,分别从串、并联系统,元件组成数量以及蒙特卡罗方法参数3个方面开展研究。结果表明:蒙特卡罗方法的可靠度计算误差可采用串联系统进行评价,尽量减少系统中的随机抽样元件个数,提高抽样数量可提高可靠度的计算精度,重复计算次数可使计算结果趋于稳定,并且单个元件抽样统计值控制可显著降低计算误差。
火工系统;可靠性预计;蒙特卡罗;计算精度
火工系统是指由数个火工元件或数个火工装置组成,同时完成两个以上(含两个)功能的组合体[1]。火工系统在设计过程中需要进行可靠性预计,根据组成系统的各单元可靠性或以往经验来推测系统的可靠性[2]。对于简单逻辑的火工系统,可通过其各单元的可靠性逻辑关系,建立精确的串并联数学模型,计算得到可靠性预计值。对于功能复杂火工系统,由于火工元件数量多、可靠性逻辑关系复杂,无法采用串并联数学模型法进行可靠性预计,可采用蒙特卡罗方法,但蒙特卡罗方法是数值计算方法,存在一定的计算误差。为提高计算精度,本研究分别从串并联系统、元件组成数量以及蒙特卡罗方法参数选择进行研究,为提升基于蒙特卡罗方法复杂火工系统可靠性预计精度提供了基础数据支撑。
1 蒙特卡罗法火工系统可靠性预计原理
火工系统是由各种元件组成,而每种元件有其固有的可靠性。当元件可靠性已知时,可以用具有元件可靠性特征参量的随机数代表产品的功能。火工系统元件的工作状态只有2种,即作用成功或失败,可以用1(成功)和0(失败)表示。利用模拟抽样代替真实抽样,系统中每个元件抽取个1,0随机数(>1 000 000),这些随机数服从二项式分布(即其中1出现的概率为该元件可靠性的值,1,0排序随机),这样就可以组成套系统。根据系统功能及元件的逻辑关系,得到这套系统最终实现功能的数量,该值在这套产品中所占的比率就是该系统的可靠性预计值。
2 串、并联系统解析解与蒙特卡罗法数值解关系
蒙特卡罗方法在计算系统可靠度时,需要将系统进行部分串并联简化,用以提高计算精度,本节分析串联系统以及并联系统中应用的计算误差。
2.1 串联系统蒙特卡罗法与数值解关系
图1为由4个元件组成的串联系统,分别采用解析解法和蒙特卡罗方法进行计算,对比蒙特卡罗方法的可靠度计算误差。

图1 4个元件组成的串联系统
该系统的可靠度计算:
=R×R×R×R=0.302 358 6 (1)
采用蒙特卡罗方法将4个元件的随机抽样分别按照其逻辑关系(图2)进行组合计算,逻辑代数表达式见式(2)。
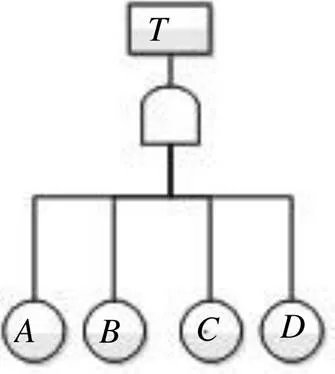
图2 串联系统的逻辑关系
=∩∩∩(2)
采用蒙特卡罗方法进行计算,其中=10 000 000,R=0.75,R=0.82,R=0.68,R=0.723。重复进行100次,对其计算精度进行验证,如图3~4所示。
从图3~4可以得到,蒙特卡罗方法计算结果在解析解附近呈现均匀分布。其计算误差在-0.1%~0.1%之间,分布均匀。
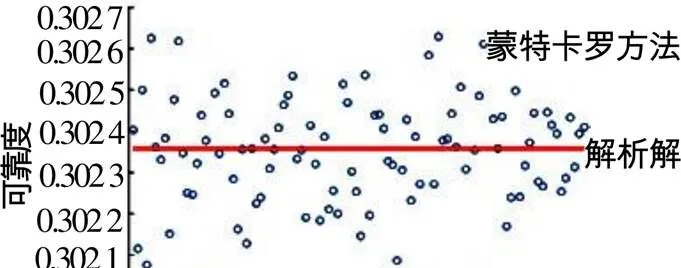
图3 采用蒙特卡罗方法计算串联系统可靠度
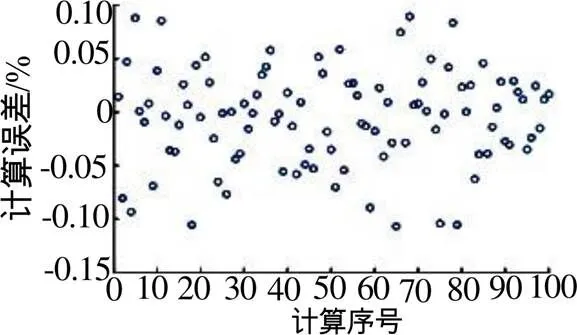
图4 采用蒙特卡罗方法计算串联系统误差
2.2 并联系统蒙特卡罗法与数值解关系
图5为由4个元件组成的并联系统,分别采用解析解法和蒙特卡罗方法进行计算,分析蒙特卡罗方法的可靠度计算误差。该系统的可靠度计算见式(3):
=1-(1-R)×(1- R)×(1- R)×(1- R) (3)
将各元件的可靠度值代入式(3)中,得到:=0.996 011 2。
采用蒙特卡罗方法将4个元件的随机抽样分别按照其逻辑关系(图6)进行组合计算,逻辑代数表达式见式(4)。
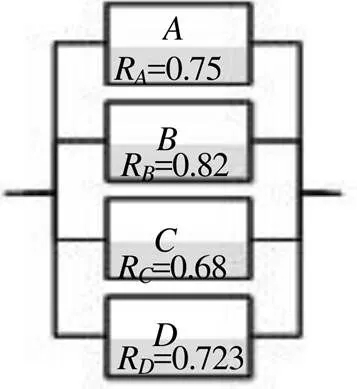
图5 4个元件组成的并联系统
图6 并联系统的逻辑关系
=∪∪∪(4)
采用蒙特卡罗方法进行计算,其中=10 000 000,R=0.75,R=0.82, R=0.68, R=0.723。重复进行100次,对其计算精度进行验证。结果如图7~8所示。
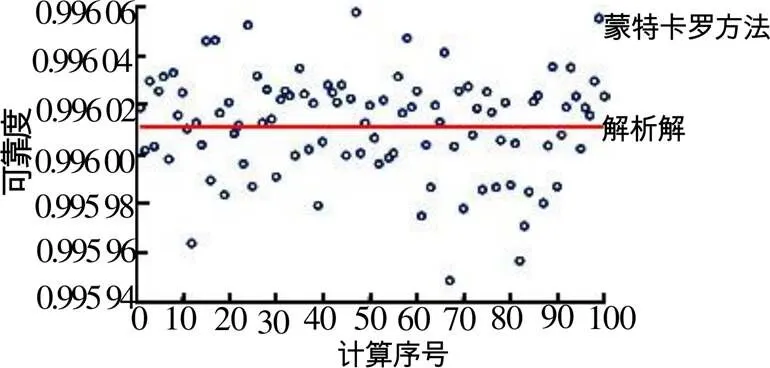
图7 采用蒙特卡罗方法计算的并联系统可靠度
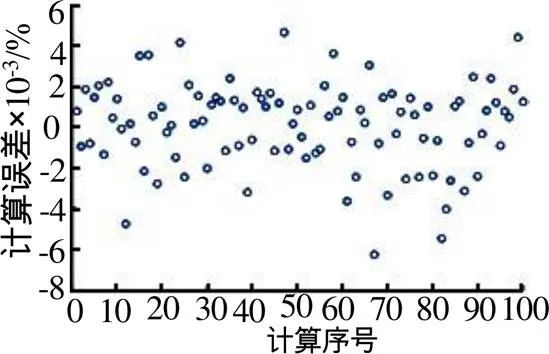
图8 采用蒙特卡罗方法计算并联系统的误差
从图7中可以得到,并联系统的可靠度在解析解附近呈现均匀分布,与串联系统一致。图8中的计算误差相比串联有很大的降低,在-0.006%~0.006%之间,分布均匀。由以上分析可以看出蒙特卡罗方法在不同系统中的计算误差是不同的,串联系统的计算误差最大,因此,对于任意系统,采用蒙特卡罗方法计算可靠度的计算误差可由该系统各元件串联组成的串联系统的误差表示。
3 系统元件组成数量对蒙特卡罗方法计算误差的影响
本研究选用串联系统,对不同数量元件组成的系统可靠度进行计算误差分析。采用元件数量分别为10,20,30,40,50,60,70,80,90,100的串联系统,进行蒙特卡罗方法的可靠度计算,元件的可靠度都设定为0.999,蒙特卡罗方法抽样数量=10 000 000,每个串联系统重复100次,对计算误差求平均值,计算结果见表1,并如图9所示。
表1 串联系统蒙特卡罗方法计算误差
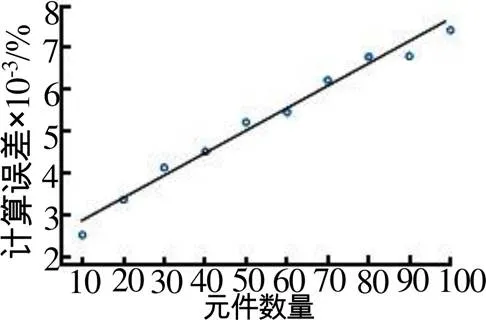
图9 不同元件数量组成的串联系统蒙特卡罗方法计算误差
从图9可以看出随着串联系统中元件数量的增加,计算误差呈现线性增长,因此控制系统中的元件数量是提高蒙特卡罗方法计算误差的有效方法。
4 蒙特卡罗方法计算精度优化
4.1 抽样数量对蒙特卡罗方法计算误差影响分析
采用元件数量分别为10,20,30,40,50,60,70,80,90,100的串联系统进行不同抽样数量下的蒙特卡罗方法可靠度计算,每个串联系统重复100次,对计算误差求平均值,结果见表2,取部分计算结果做图,如图10所示。
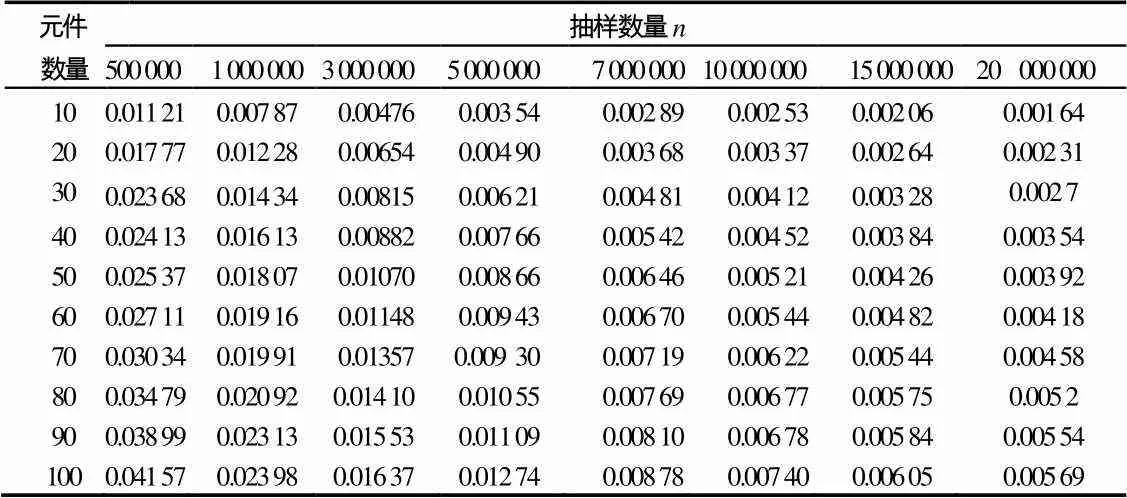
表2 不同抽样数量蒙特卡罗方法计算结果
Tab.2 Monte Carlo calculation results of different sampling numbers
从表2计算结果及图10可以看出,抽样数量越大,蒙特卡罗方法计算可靠度的计算误差越小,受到计算机的内存限制,本系统可靠性预计时,选取=10 000 000的抽样样本。
4.2 蒙特卡罗方法重复计算次数与计算误差关系
由于多次重复进行蒙特卡罗方法的计算所得到的可靠度是均匀分布在解析解附近,对其求平均值后可以让蒙特卡罗方法计算的可靠度更接近于解析解。本节针对蒙特卡罗方法重复次数对计算误差的影响问题进行分析,得到适用于本项目计算的重复次数。选取不同抽样数量,分别重复次计算,计算结果如图11所示。
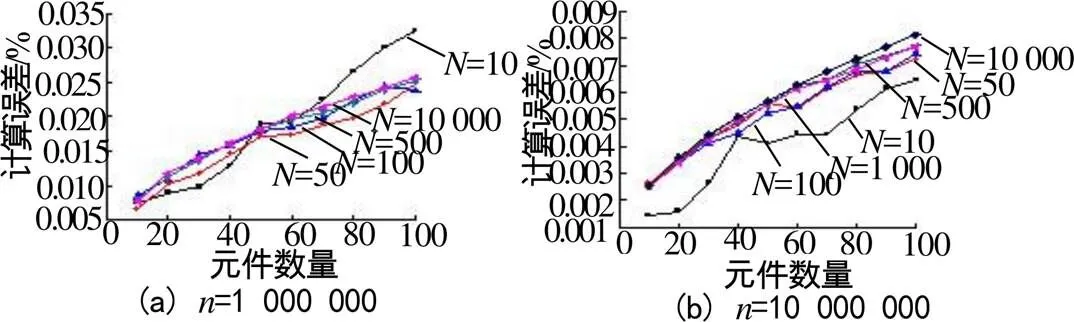
图11 蒙特卡罗方法不同计算次数的计算误差曲线
从图11可以看出,蒙特卡罗方法计算次数(求平均值)的增加并不能降低其计算误差,只能让其计算误差更趋于稳定,趋向于真实误差。
4.3 单个元件抽样统计值控制分析
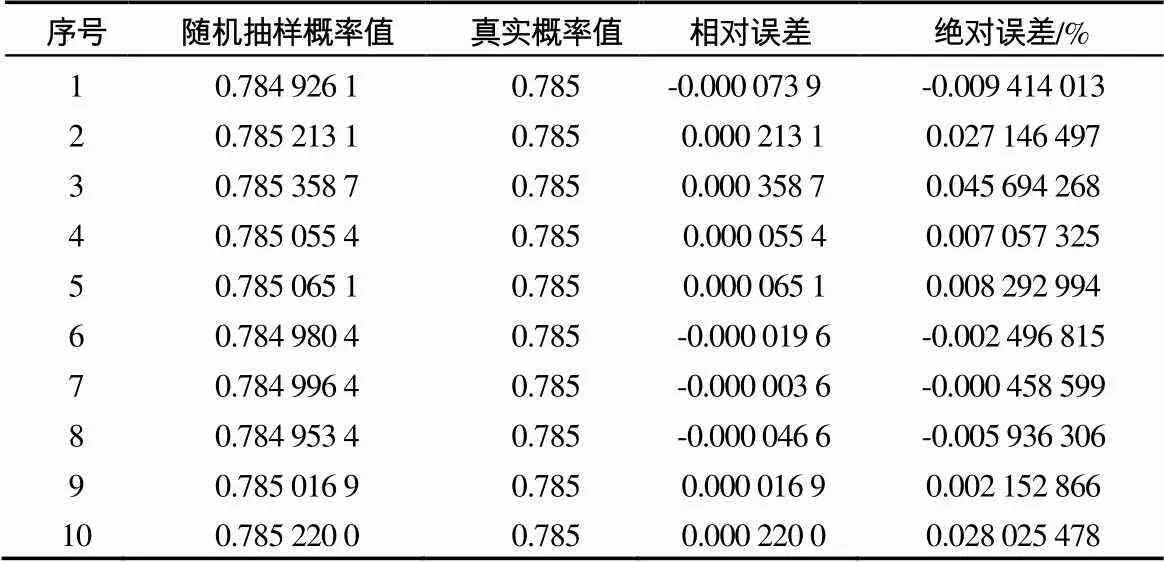
在随机数抽样时,抽样的随机数与真实规定的概率存在一定误差,如元件的可靠度为0.785,随机抽取10 000 000个样本,重复10次的结果如表3所示。
表3 随机抽样概率值误差举例
Tab.3 Examples of random sampling probability value errors
表3中随机抽样概率值为随机抽取10 000 000个样本中1所占的比率,其值非常接近真实概率值0.785,但存在一定的误差,最大误差可大0.045 6%,将这样的随机数带入蒙特卡罗方法中进行计算,在多个元件组成的系统中,计算误差进行累积,结果的计算误差相对较大,因此需要降低随机抽样概率值与真实值的计算误差。本节采用随机数绝对误差限制的方法,降低随机抽样概率值的误差,从而提高系统可靠度的计算精度,计算结果如图12及表4所示。从表4及图12可以看出对随机数进行绝对误差控制可以大幅降低计算误差,采用绝对误差控制在10-6后,系统组成单元数在100个以内的绝对计算误差降低至0.001 89%以内。
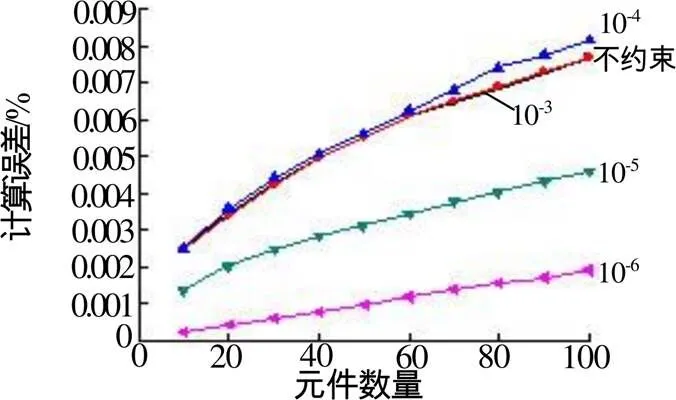
图12 各绝对误差控制情况下计算误差曲线图(n=10 000 000)
表4 各绝对误差控制情况下计算误差结果
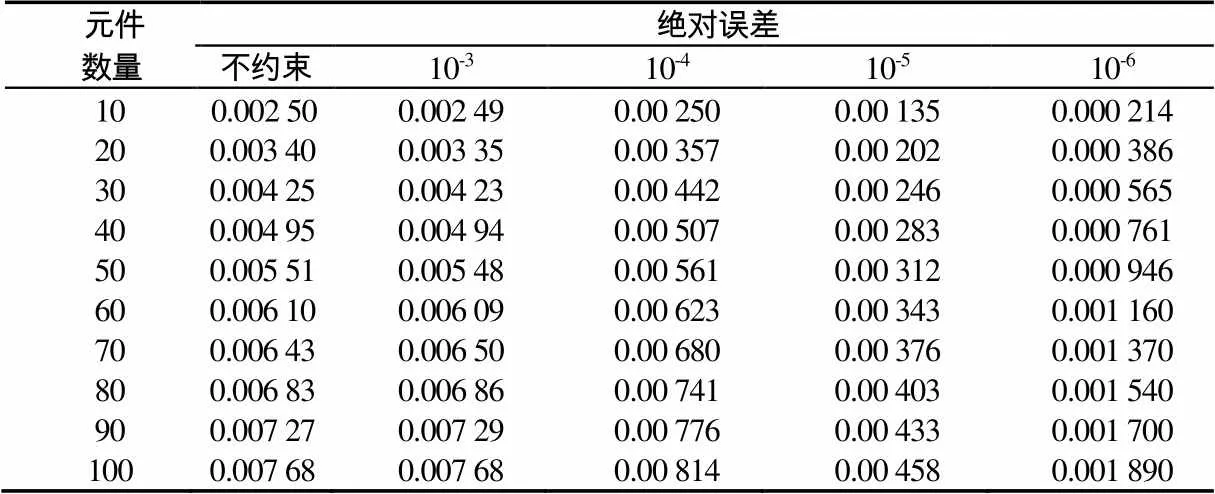
Tab.4 Calculation error results for each absolute error control
5 结论
(1)研究表明,采用蒙特卡罗方法在串联系统中的计算误差最大,因此可将系统中的元件进行串联,分别计算解析解和仿真值,得到的计算误差为该系统的最大误差。(2)串联系统元件数量与蒙特卡罗方法计算误差呈现线性关系,应尽量减少系统中的随机抽样元件个数。(3)提高抽样数量可提高可靠度的计算精度,但受到计算机内存及计算时间的限制,建议取抽样数量为=10 000 000。(4)蒙特卡罗方法重复计算次数可使计算结果趋于稳定,建议计算次数选择=1 000。(5)单个元件抽样统计值控制对降低蒙特卡罗方法计算误差有非常显著的作用,建议随机数抽样绝对误差限制在10-6。
[1] 王凯民.火工品工程[M].北京:国防工业出版社, 2014.
[2] 李进贤.火箭发动机可靠性[M].西安:西北工业大学出版社, 2000.
[3] 徐凤一,张蕊,贺爱峰,陈建华,井波,曹椿强.激光火工系统用脉冲激光器可靠性研究[C]//第十六届中国科协年会论文集,2014.
[4] 严楠,蔡瑞娇,田玉斌.感度试验Monte-Carlo法的计算机模拟与分析[J].火工品,1995(4):1-6.
Research on Reliability Prediction Accuracy of Complex Initiators System Based on Monte Carlo
FU Dong-xiao,ZHANG Guo-xing,ZHANG Rui,LI Fang,DU Zhen-hua,MA Hong-liang,PING Chuan
(Science and Technology on Applied Physical Chemistry Laboratory, Shaanxi Applied Physics and Chemistry Research Institute, Xi’an, 710061)
In order to solve the problem of error in the reliability prediction process of complex initiators system for Monte Carlo method, the reliability prediction calculation is studied from three aspects: series and parallel system, component quantity and Monte Carlo method parameters. The results show that Monte Carlo method reliability calculation error can be evaluated by series system, and the number of random sampling components in the system should be minimized, as well as increasing the number of samples. Meanwhile, the number of repetitions of Monte Carlo method can make the calculation result stable, and the single-element sampling statistical value control has a very significant effect on reducing the calculation error.
Initiator system;Reliability prediction;Monte Carlo;Calculation accuracy
TJ450.2
A
10.3969/j.issn.1003-1480.2019.05.008
1003-1480(2019)05-0029-04
2019-07-19
付东晓(1981-),男,高级工程师,从事火工品安全性可靠性技术研究。

