基于双测量机器人的土石坝表面变形自动化监测技术研究

杨明化，汪少青，高 全

（1.国家大坝安全工程技术研究中心，湖北武汉 430010；

2.长江勘测规划设计研究有限责任公司，湖北武汉 430010；3.花凉亭水库管理局，安徽太湖 246400）

1 研究背景

大坝安全责任重于泰山，作为掌握大坝安全重要途径的大坝安全监测日益受到重视，对大坝安全监测技术也提出了更高要求。土石坝占我国水库大坝总量90%以上，其表面变形监测作为重要安全监测项目，是掌握土石坝大坝安全性态的重要途径之一［1］。监测方法包括自动化监测和人工观测，其中真空激光准直法、引张线法、自动化垂线仪、GNSS法等现有常规变形自动化监测方法，存在成本高、适应性差、精度低或运维难等问题，难以适应土石坝变形监测要求［2-3］。几何水准法、三角高程法、视准线法、极坐标法等常规人工观测方法，方法简单、精度高，但观测劳动强度大、效率低。目前，大坝表面变形监测主要依靠人工观测，采用几何水准法和视准线法完成，劳动强度大、效率低，不能适时自动观测，难以满足监测发展需求。

自动化监测可对测点进行高频次自动监测，并可利用监测模型快速分析和评估大坝安全性状，为大坝安全管理提供及时有效的支撑［4-5］。随着高精度智能型全站仪的广泛应用，带有CCD摄像机和马达伺服机构的测量机器人，可实现自动精确照准、自动观测、自动记录和数据转换。测量机器人观测大坝表面变形存在测量精度不足问题，主要是受大气折光系数的误差以及仪器高、棱镜高量取误差等影响［5］。若能降低甚至消除这些误差，就能直接且有效提高测量精度，从而满足大坝表面变形自动化观测精度要求，而双测量机器观测模式对于降低甚至消除这些误差具有明显优势。此外，安全监测规范明确要求，土石坝水平位移和垂直位移宜同步观测。因此，研究双测量机器人观测模式，发挥测量机器人自动观测和精度优势，同步观测土石坝水平位移和垂直位移，满足监测精度要求，对实现土石坝表面变形自动化观测具有重要意义。

2 双测量机器人观测系统

测量机器人（Measurement Robot）是一种智能型电子全站仪，能自动进行搜索、跟踪、辨识和精确照准目标，并获取角度、距离、三维坐标以及影像等信息［6］。在全站仪的基础上，智能型电子全站仪的研发集成了激光、精密机械、微型计算机、CCD传感器以及人工智能技术。在计算机控制下，机器人可自动识别目标、精确照准、自动记录测量数据，无接触自动遥测目标，且不受白天黑夜影响。目前主要测量机器人包括徕卡TM、TS系列，测角精度0.5″，测距精度为±（0.6+1ppm）mm。

土石坝表面变形监测点一般采用断面形式布置，包括平行于坝轴线方向的监测纵断面和垂直于坝轴线方向的监测横断面。其中，监测纵断面一般不少于4个，断面有直线、曲线等形式；监测横断面一般不少于3个，布设在最大坝高或原河床处，合龙段、地形突变处、地质条件复杂处等，断面上各监测点高程相差较大。根据土石坝表面变形监测点的布置要求，监测点布置存在测线或直或曲、测点分散、高差较大等特点。根据土石坝测点分布特点，在传统变形观测手段基础上，发挥测量机器人优势，提出双测量机器人观测系统，并减少观测误差，大幅度提高观测精度，适应土石坝表面变形自动化观测。

双测量机器人观测系统主要由基站、基准点、监测点组成，见图1。通过测量机器人、传输系统、控制系统、数据分析软件等系统来实现自动化监测。测量机器人基站由观测墩、测量机器人、观测房组成，布设在大坝左右岸稳定山体上。测量机器人架设于基点上，为坐标原点，要求基础稳定、通视条件良好，仪器标高固定。基准点位于变形区以外的稳固处，布设有观测墩和特制棱镜，与坝区基准点一起组成控制网，为系统数据处理提供基准。监测点分布在土石坝表面，反映监测目标的变形状态。监测点由观测墩、正对基站的棱镜、数字式温度计和气压计组成；根据工程实际和规范要求，较均匀地布设于变形体有代表性的横纵断面上。测量机器人变形监测布置情况见图2。采用双测量机器人系统，通过两个测量机器人同时对向观测监测点的变形情况，并利用数值分析方法，减少观测误差。其中，垂直位移观测采用三角高程法，进行对向三角高程测量；水平位移观测采用极坐标法，进行对向极坐标测量。

图1 双测量机器人观测系统

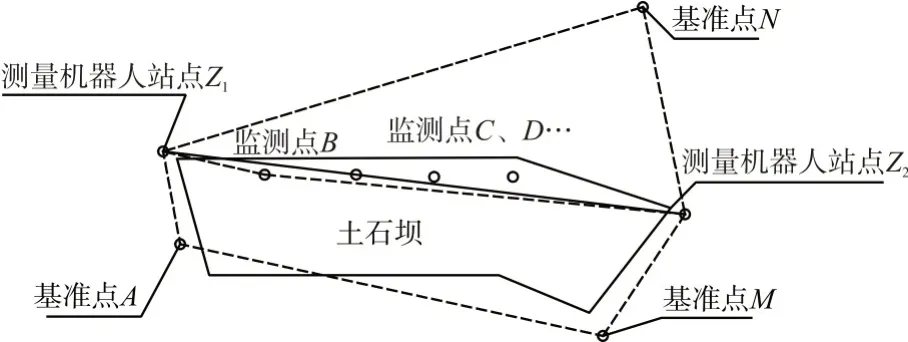
图2 测量机器人变形监测布置

3 双测量机器人垂直位移观测

3.1 对向三角高程测量原理

三角高程测量是观测测站向照准点的高度角和两点间的斜距，运用三角公式计算两点间高差的方法。三角高程测量误差主要有仪器测角误差、仪器测距误差、大气折光系数、仪器高和棱镜高测量误差等，其中，测角和测距误差随着仪器测量精度的提高有效减少。目前制约测量精度的主要因素是大气折光系数、仪器高以及棱镜高量取误差。

对向三角高程测量基于三角测量原理，在两基准点处分别设置一台相同型号测量机器人，同时对向观测基准点和监测点，间接测量起终点的往返高差，进行大坝垂直位移监测，见图3。

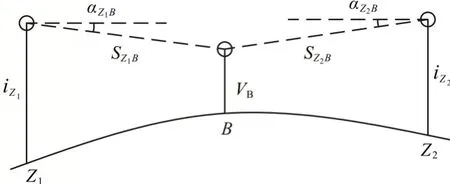
图3 双测量机器人对向三角高程测量示意

结合图2和图3，基准点A和N上摆放的是同一个带棱镜特制基座，设其棱镜中心到基准点的高差为vA。Z1站测量机器人仪器高为iZ1，观测棱镜A的竖直角为αZ1A，斜距为SZ1A；观测棱镜B的竖直角为αZ1B，斜距为SZ1B。 Z2站测量机器人仪器高为iZ2，观测A 点的竖直角为αZ2A，斜距为SZ2A；观测棱镜B 的竖直角为αZ2B，斜距为SZ2B，棱镜的高度为vB。Z1、Z2到A、B点的高差公式为

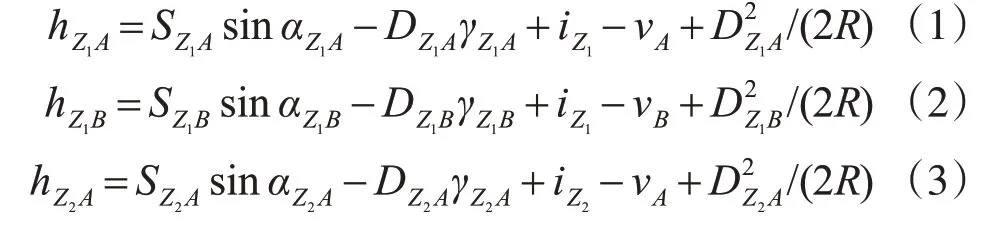
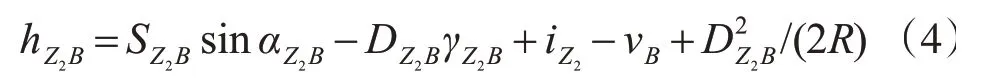
式中，D 为A、B 间的水平距离；R 为地球的曲率半径；γAB为垂直折光角度，γAB=KABD2/(2R)；KAB为大气垂直折光系数。

由式（1）～（4），可以分别计算A到B的高差和B到A的高差，再取其平均值作为AB间的高差，即：

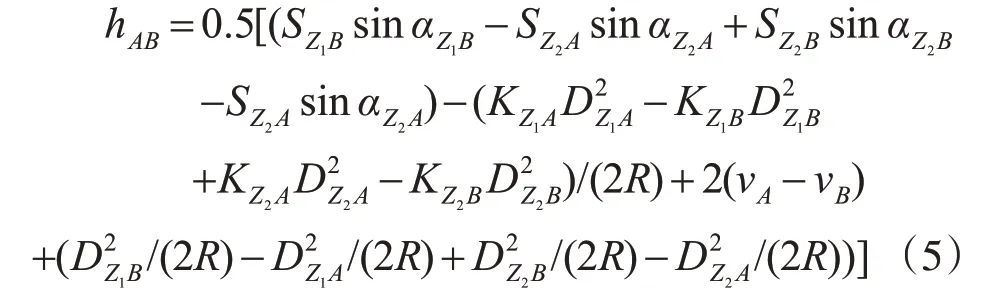
大坝表面变形监测范围相对地球半径不大，由Z1站和Z2站位置关系可知：，且可以认为大气折光系数对观测点和基准点的影响相同，即。则有：

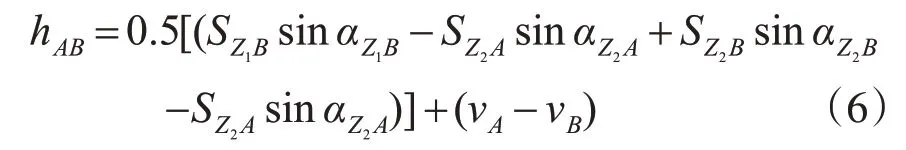
根据式（6）即可计算测点B与基准点A的高差，对监测点B 进行垂直位移观测，同时消除了大气的折光影响以及测量机器人仪器标高的影响。同理，可以观测大坝表面的C、D等各监测点的垂直位移。

3.2 对向三角高程测量精度分析

根据对向三角高程测量基本计算公式（6），由误差传播定律推得高程观测中误差公式为

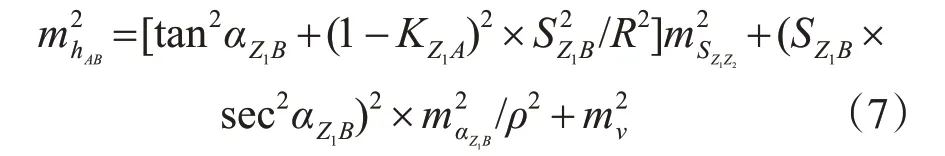
式中，mSZ1Z2为测边中误差；mαZ1B为垂直角中误差，两者因测量机器人和观测测回值不同而有所区别；mv为仪棱镜高程中误差。参照文献［7］和［8］可知，选择A-B 高差测量为例，利用2 台TS30 测量机器人，通过基准点Z1、Z2采用对向三角高程法对象观测。利用二等水准的高差检测三角高程的高差，根据规范要求两者较差的限差应小于±6 L mm（L 为测段长，以km为单位）。对比三角高程测量和水准测量高差较差，三角高程往返高差统计见表1，三角高程测量与水准测量高差较差比较见表2。

比较两个测段的三角高程高差与水准高差，两测点间往返高差最大绝对值仅为1.14 mm，文献［8］中往返较差最大也仅1.49 mm，均小于限差要求，即对向三角高程测量精度可达二等水准的要求。

表1 三角高程往返高差统计

表2 三角高程测量和水准测量高差较差比较

综上，采用双测量机器人同时对向观测，间接观测大坝垂直位移，消除了大气折光和地球曲率的影响，且无需测量仪器高度和棱镜高程即可得到测点高程，观测精度达到二等高程测量的精度，适应并满足土石坝表面垂直位移观测。

4 双测量机器人水平位移观测

4.1 极坐标测量原理

极坐标法是监测大坝水平位移常用的观测方法，基本原理为从已有控制点用一个角和一段距离测设点的平面位置。采用极坐标法测量需选择通视情况良好、受环境影响较少的观测条件，在许多工程中是首选的观测方法，尤其是观测点数量多且分散的情况。为提高水平角观测精度，应选择距离适中、成像稳定的条件作为后视点，尽量避免短边作为后视点，以减小测点对中及目标偏心误差对水平角观测带来的影响。

双测量机器人极坐标测量原理为：在两基准点分别设置一台同型号测量机器人，相互观测进行绝对定向和相对定向，求得观测初始参数（两基点间距和高差）；调整其观测参数后，再分别观测测点的水平角和垂直角，按空间交会原理，得到观测点的坐标，即可观测大坝水平位移。

图2 和图4 中，两测站Z1、Z2，α、θ 分别为测站观测测点的水平角和垂直角。按空间交会原理，可得观测点B的坐标为

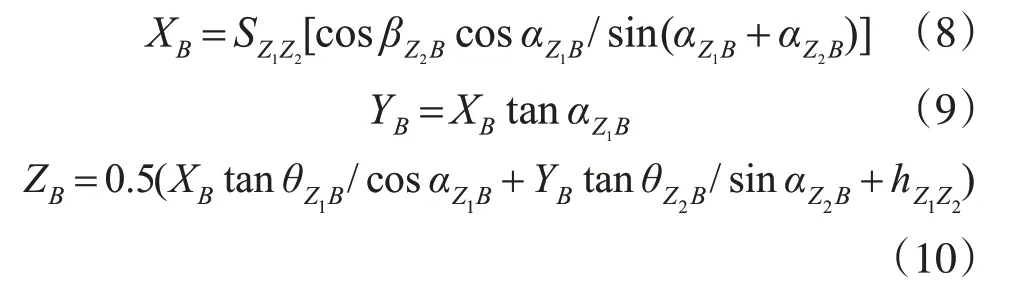
图4 双测量机器人极坐标水平位移测量示意

式中，SZ1Z2为两测站的间距；hZ1Z2为高差；K 为大气垂直折光系数。

根据式（8）～（10）观测监测点B的坐标，即可计算监测点B的水平位移。通过双测量机器人观测与计算，可减弱或消除大气折光、气温、气压等共同误差，提高测量精度。

4.2 极坐标测量精度分析

两台测量机器人进行定向观测，能实现全自动化观测，水平位移量中误差限值不超过±0.1 mm。

5 结 论

（1）充分利用测量机器人特点，基于三角高程法和极坐标法，进行双测量机器人对向观测，可实现大坝表面水平位移和垂直位移同步自动化观测，满足大坝安全监测自动化的发展要求，具有推广应用价值。

（2）双测量机器人对向三角高程测量，适应土石坝垂直位移观测，可有效地消除大气折光和地球曲率的影响，且可以达到二等水准测量的精度。

（3）双测量机器人极坐标水平位移观测，适应土石坝水平位移观测，可减弱或消除大气折光、气温、气压等共同误差，水平位移量中误差限值不超过±0.1 mm。

由误差传播定律，根据计算公式（8）～（10），可得目标点B的坐标分量精度指标为

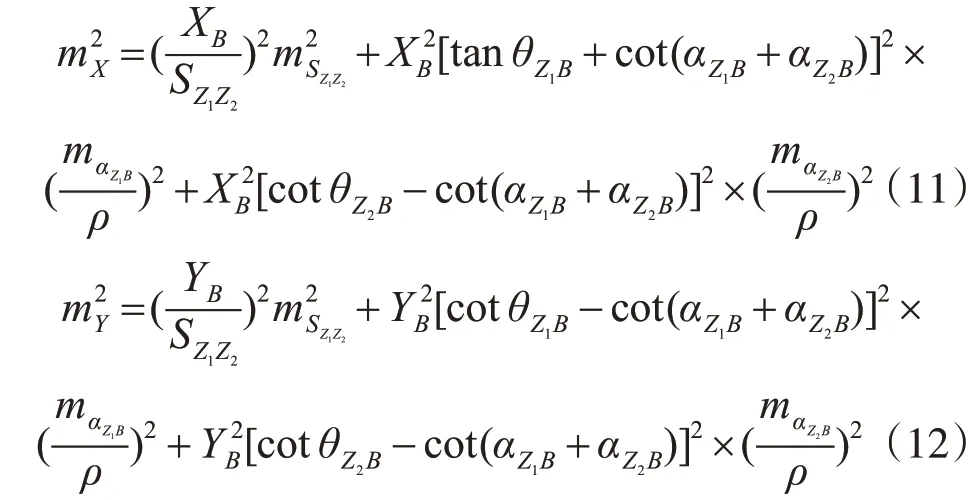
式中，mSZ1Z2为基线SZ1Z2的中误差；mhZ1Z2为两仪器高差的中误差；mαZ1B、mαZ2B为水平角中误差；mθZ1B、mθZ2B为垂直角中误差。

参考文献［9］和［10］，通过基准点Z1、Z2共同观测监测点B，共4个测次、8个测回，方向与边长精度见表3。

表3 方向与边长精度

根据公式（8）～（12），可以计算测量中误差为mX=0.038 mm ，mY=0.066 mm 。由此可看出，由