考虑电网特性的调压室临界稳定断面研究
何志锋,彭志远,何 峰,桂绍波
(长江勘测规划设计研究有限责任公司,湖北武汉 430071)
对于具有长引水管道、复杂布置形式和担负重要调峰调频任务的水电站,从小波动的角度通过改善调节系统的稳定性和调节品质以满足电站安全稳定运行和供电质量的要求,需要采用平压措施——设置调压室[1]。
对于调压室的布置问题,学术界有大量研究:调压室临界稳定断面积最早由D.Thoma 于1910 年提出[2],即著名的托马公式。克里夫琴科[3]认为选择适当的调速器参数,在调压室断面积小于托马断面积的情况下,系统也能稳定运行。杨建东等[4-5]研究了上、下游双调压室系统波动稳定性问题,提出了上、下游双调压室临界稳定断面的合理配置准则。郭文成等[6]将压力管道水流惯性和调速器特性引入调压室临界稳定断面研究。然而以上研究考虑的只是水电站孤网运行的情况,对水电站并网运行的情况未有涉及。而现代电力系统中水轮发电机组孤网运行只是一种事故性和暂时的运行方式,并网运行才是其主要的运行方式。文献[7]对电网、调压室联合作用下的水轮机调节系统暂态特性的研究表明,电网对调节品质有改善作用,且并入规模较大的电网运行的水轮机调节系统,仅需一个断面积较小的调压室亦可达到稳定,但文献[7]仅依靠数值模拟的手段来研究,理论上的分析不够充分。
本文从理论上对考虑电网特性的调压室临界稳定断面进行研究,定量定性地分析电网对调压室临界稳定断面积的影响,探讨电网对调节品质改善作用的内在机理,对接入高安全等级、有限规模电网水电站的调压室的合理布置具有一定参考意义。
1 数学模型
1.1 边界条件
并网条件下带调压室水电站引水发电系统如图1所示。为便于研究分析,本文假设:①忽略水体和管壁的弹性,引水隧洞和压力管道都采用刚性水击模型[8];②忽略调压室底部水头损失和流速水头;③小波动过渡过程采用稳态工况点局部线性化的方法,用水轮机的6 个传递系数来表述水轮机稳态特性[9];④调速器采用频率调节模式,忽略其非线性特性:饱和特性和转速死区;⑤负载扰动仅为阶跃扰动;⑥电网模型采用D.H.Thorne 和E.F.Hill 提出的线性化模型[10],将电网表示为一个等效的发电机组;⑦不考虑电流、电压及其暂态、次暂态等高频非线性电气参数。
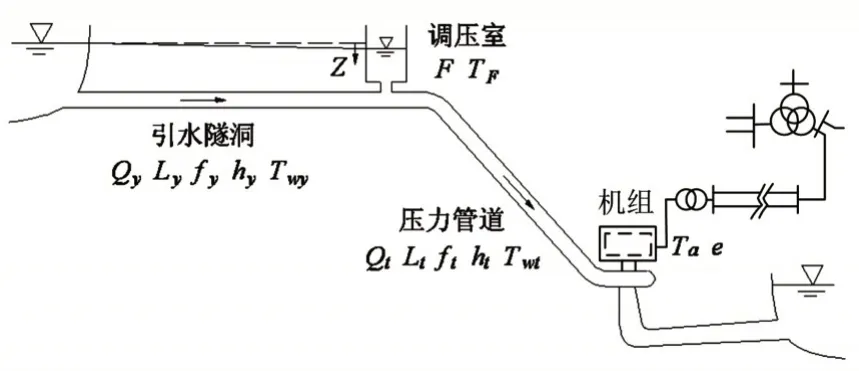
图1 并网条件下带调压室水电站引水发电系统示意
1.2 引水系统基本方程
水力系统反映了工作水头H与工作流量Q的关系,本文采用刚性水击模型,其基本方程如下:引水隧洞动力方程:

调压室连续性方程:

压力管道动力方程:

上述式中,z 为调压室水位变化相对值;H0为机组初始工作水头;qy,qt和h分别为引水隧洞流量、机组引用流量和机组工作水头变化相对值;hy0,ht0为引水隧洞和压力管道的水头损失;TF为调压室时间常数;Twt为水流惯性时间常数。
1.3 水轮机基本方程
力矩方程:

流量方程:

上述式中,x,y,mt,qt分别为水轮机转速、导叶开度、力矩和引用流量变化相对值;eh,ex,ey为水轮机力矩传递系数;eqh、eqx、eqy为水轮机流量传递系数。水轮机传递系数取理想值:eh=1.5,ex=-1,ey=1,eqh=0.5,eqx=0,eqy=1。
1.4 调速器系统基本方程
本文采用频率调节模式,不考虑调速器电液随动系统中诸如死区特性、饱和特性等非线性因素,假设调速器环节为线性环节,基本方程如下:
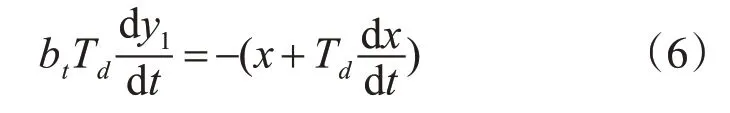
接力器的运动速度与配压阀开口并不是理想的线性关系,存在一定的非线性[11];接力器反应时间常数Ty等于接力器速度特性曲线某点斜率的倒数,而本文采取平均斜率方法来确定Ty的大小。仅考虑主接力器的作用,不考虑辅助接力器及局部反馈机构的作用,得出接力器方程如下:

式中,bt、Td和Ty分别为调速器暂态转差系数、缓冲时间常数和主接力器时间常数。
1.5 并网发电机基本方程
在并网条件下,忽略电网频率偏差Δxs和母线电压偏差ΔVt,在发电机一阶模型基础上,结合转速x与功角δ 之间的关系[12],则发电机方程最终表示为

式中,Ta为机组惯性时间常数;mg0为初始时刻负荷相对变化值;eg为电网自调节系数。
1.6 电网模型
根据文献[10]和[13],电网模型可表示为如图2所示:
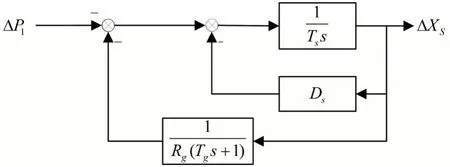
图2 电网模型框
图2 中,ΔP1是电网遭受的负载扰动;Ts是电网等效机组惯性时间常数,包括电网中所有机组的旋转惯性效应,其值体现了电网规模的大小;Ds是电网等效负荷自调节系数,描述了电网负荷与频率之间的阻尼特性,对于一定程度的频率偏差,Ds决定了相应的功率变化,Ds值通常较难精确测得,但与电网规模表现出一定的正相关性[14]。另外,项表示电网等效调速系统,它综合了电网内所有机组调速系统的动态特性,其中,Tg为电网等效接力器惯性时间常数;Rg为电网等效永态转差系数,由电网内所含机组的永态转差系数epi共同决定,满足如下关系:;由于本机额定功率基值与系统额定功率基值不同,因此还需要通过一个转换系数B将两者相连。
1.7 并网条件下的水轮机调节系统
通过对1.1~1.6节的整理,可得出并网条件下的水轮机调节系统方框图,如图3 所示。整理可得出并网条件下调节系统模型的综合传递函数:

2 考虑电网特性的临界稳定断面分析
对于一种调节模式,只有当霍尔维茨(Hurwitz)判据中的所有不等式判据同时成立时,调节系统才是稳定的[15],托马稳定条件只是所有并列的不等式判据中的一个,因此该判据仅为系统稳定的一个必要条件。临界稳定断面可由这一个判据在取等号时求出,可称此判据为临界稳定断面判据。
2.1 公式推导
依照托马断面的求解方法[2],令q1=0,可得并网下的考虑电网特性的托马断面公式:

其中,
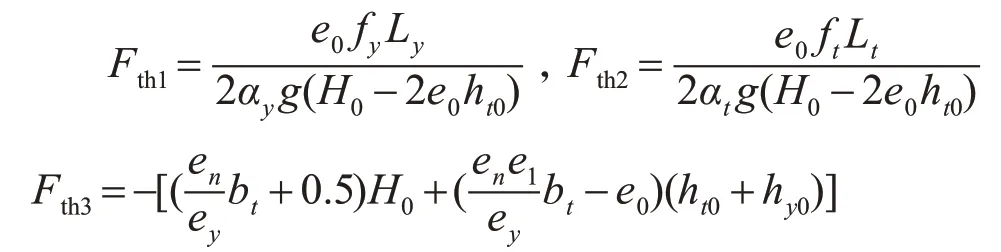

为水轮机特性传递系数。
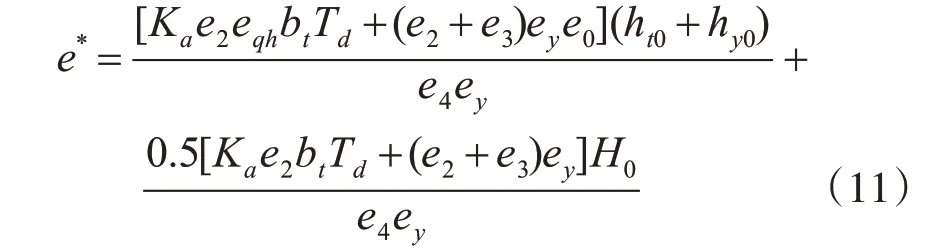
由文献[6]可知,Fth1,Fth2,Fth3分别为考虑水轮机特性的引水隧洞水流惯性项、考虑水轮机特性的压力管道水流惯性项和水轮机特性的调速器特性项,Fth1+Fth2+Fth3=Fthiso是孤网运行下的考虑压力管道水流惯性和调速器特性的调压室临界稳定断面公式;只有Fth4包含电网参数,因此本文将Fth4称为考虑水轮机特性的电网调节特性项。
同理,本文将e2,e3,e4称为电网调节系数项,将e*称为调压室托马临界断面电网调节系数项。
2.2 实例分析
下文给出了中、高、低水头的3个水电站的比较分析,分别以水电站A、水电站B、水电站C 为例,各电站基本资料见表1。
本文给出3 组电网:电网a,电网b,电网c,其电网规模依次逐步增加。电网具体参数见表2。
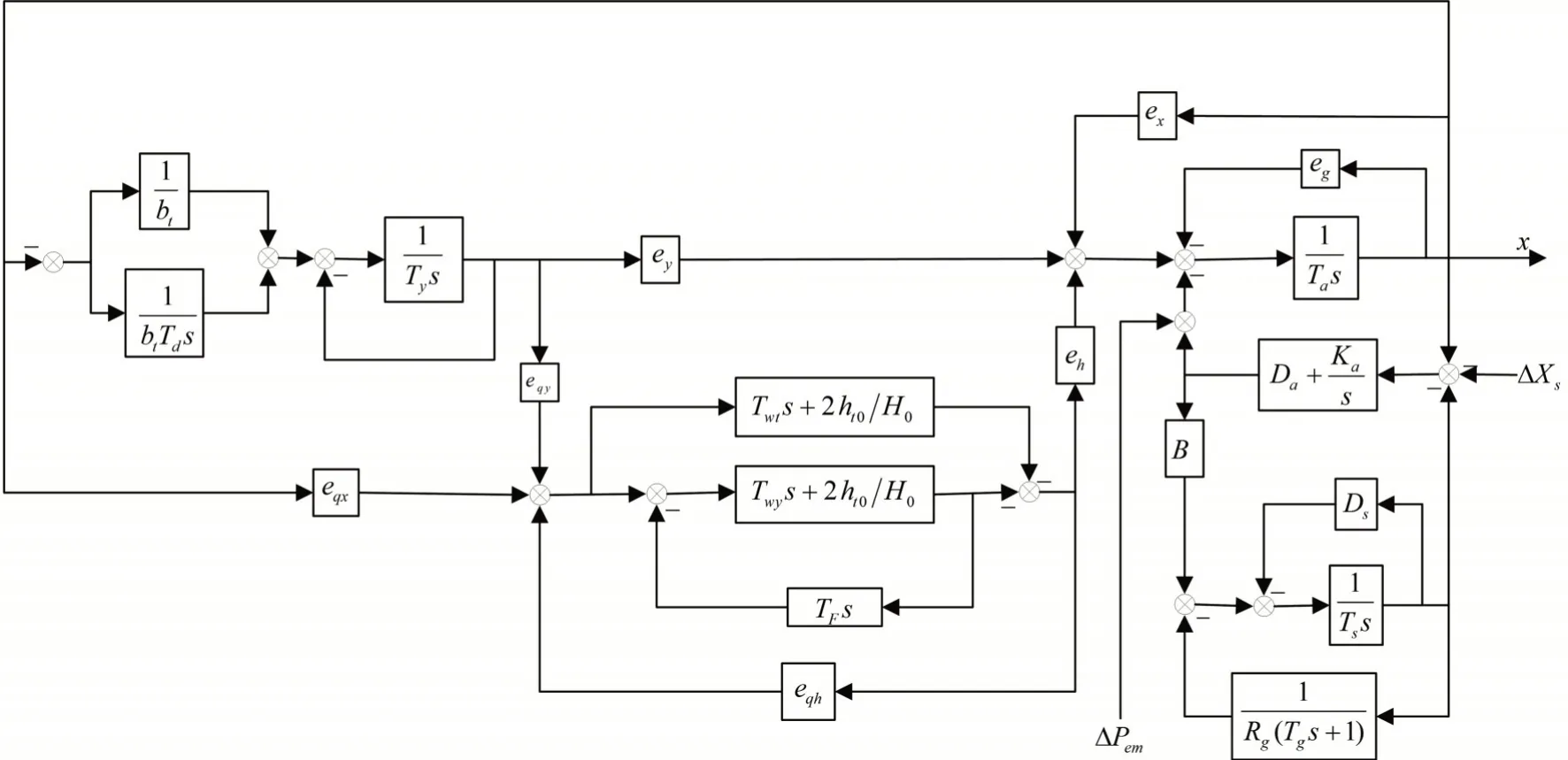
图3 并网条件下的水轮机调节系统方框
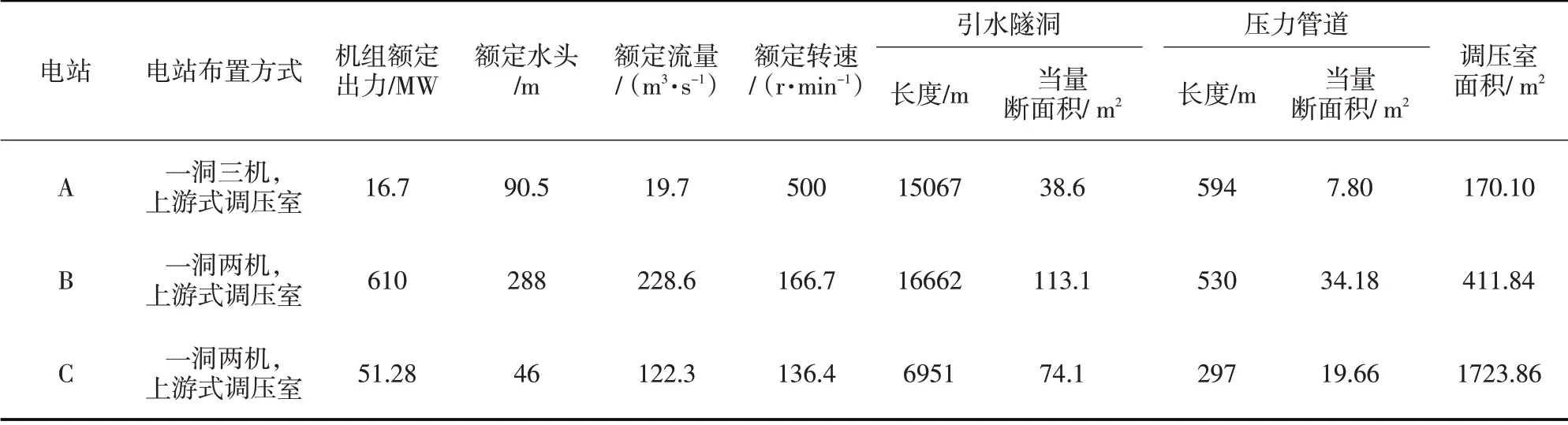
表1 水电站A、水电站、水电站C的基本参数
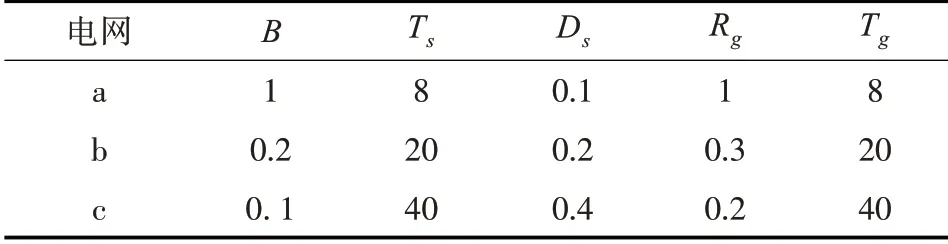
表2 三组电网参数对照 s
水电站A、水电站B、水电站C在不同bt,Td,eg下,并入不同规模电网的Fth1,Fth2,Fth3,Fth4,Fthcon如表3所示。
由表3可知:
(1) Fth1>0 ,Fth2>0 ,Fth3<0 ,Fth4<0 ,且Fth1+Fth2>Fthcon,说明调速器特性项和电网调节特性项可以减小托马断面面积,即调速器调节和电网调节对水轮机调速系统调节品质均有改善作用;又有 ||Fth3< ||Fth4,特别是在电网b与电网c中,可见电网调节的改善作用较调速器调节的改善作用更为显著。再对比Fthiso和Fthcon,由于Fth4<0 ,可得Fthcon<Fthiso,从公式层面阐释了并网条件下的调速系统所需的调压室断面积较孤网系统小,亦在理论上定性证明了电网对水轮机系统调节品质有改善作用,使其更易稳定。
(2)同一水电站,在bt,Td、eg一定的条件下,随着所并入的电网类型的改变,Fth3不变,说明电网参数的改变对Fth3无影响;而 ||Fth4随着电网规模的增大而显著增大,定量地说明了水轮机调速系统所并入的电网规模越大,电网对其调节品质的改善作用越明显。
(3)同一水电站,所并入电网类型不变的情况下,随着bt,Td的改变,Fth3、Fth4均有改变:随着bt,Td的增大, ||Fth3、 ||Fth4增大,且 ||Fth3增大的幅度较 ||Fth4更为显著;随着eg的改变,Fth3有所变化而Fth4保持不变。
由Fth4的表达式可知,电网对水轮机调速系统的改善程度完全取决于e*,而e*与电网参数B 、Ts、Ds、Tg、Rg有关,与eg无关;且e*越大,改善效果越好。为进一步探究电网改善调节系统调节品质的内在机理,下面对e*分别关于B、Ts、Ds、Tg、Rg进行求导,为便于分析,假设ht0=0,hy0=0,求导结果见表4。
可以得出以下结论:B 越小、Ds越大、Tg越大、Rg越小,e*越大,系统的托马稳定断面越小,而Ts对托马临界稳定断面无影响;Ds、Tg对e*的变化率无影响,即e*和Ds、Tg呈正相关,而由可知B、Rg越小,e*随B、Rg减小而增加的变化率的绝对值也越大,即B、Rg对托马临界稳定断面影响越显著。一般并网情况下,B <1、Rg<1、btTd>1,则由此可判断出:在并网运行条件下,B、Rg对e*影响最大,Ds次之,Rg再次之,而Ts无影响。

表3 水电站A、水电站B、水电站C的Fth 1,Fth 2,Fth 3,Fth 4 详情

表4 e*分别关于B、Ts、Ds、Tg、Rg 求导结果
3 结 论
本文推导了考虑电网特性的调压室临界稳定断面公式,从公式层面阐释了并网条件下的调速系统所需的调压室断面积较孤网系统小;定性地证明了电网对水轮机系统调节品质有改善作用,定量地分析了5个电网参数各自对考虑电网特性的调压室临界稳定断面的影响程度:在并网运行条件下,B、Rg对e*影响最大,Ds次之,Tg再次之,而Ts无影响。

