基于NMF特征提取的调节阀故障诊断
孟永毅
(山西鲁能河曲发电有限公司,山西 忻州 036500)
0 引言
对于火电机组中任意一个基本的控制回路,调节阀的好坏直接决定整个回路的运行效率, 继而影响其他相关参量的变化。据不完全统计,调节阀的投资占每台机组总投资的10%左右, 而机组大约60%的故障来源于调节阀的各种故障与劣化, 所以针对调节阀的故障检测与诊断具有重要的意义与研究价值。
针对调节阀的故障检测与诊断研究, 早期从建立数学模型的角度出发, 然而这种基于精准数学模型的方法需要对系统深入理解,而在实际应用中,尤其针对复杂系统的情况有时甚至无法完成该工作[1-4]。基于此通过定性分析认知调节阀故障的研究应用,并取得了相应的成果,但是在实际生产过程中,有些先验知识的获取比较困难或者需要消耗很大的成本。 基于数据驱动的检测方法无论是在模型获取还是特征提取方面都具有优越的性能, 故而本文采用非负矩阵分解方法进行降维和特征提取,配合BP 神经网络实现调节阀的故障检测与诊断。
非负矩阵分解作为一种新兴的多元统计方法,与传统的主元分析、独立主元分析等相比,具有很好的鲁棒性、稀疏性。 该方法在分解矩阵的过程中,要求数据矩阵以及分解结果保持非负, 使得分解因子天然具有稀疏性的特点, 而分解得到的两个低维矩阵分别作为基矩阵和系数矩阵, 则原矩阵即可表达为基矩阵中的样本特征, 通过系数矩阵表示。 文献[5]利用非负矩阵分解优越的提取局部特征的能力,对发动机故障信号进行处理并得到更高的分类精度。 文献[6]将非负矩阵分解与支持向量机相结合,用于研究复杂化工过程的故障诊断并在TE 数据平台加以仿真实践,验证方法的有效性。 文献[7]在传统分解方法的基础上提出了广义非负矩阵投影算法,拓宽了数据适用范围,并类似PCA 建立监测统计量指标来检测故障的发生。
神经网络具有较强的非线性映射能力、 学习能力和容错能力。 通过神经网络的构建、训练、分类来完成故障诊断。 国内外学者利用神经网络技术对调节阀的故障诊断作出大量研究工作。文献[8]通过自回归方法对止回阀故障状态的声波信号进行分析,发现声波频率、 回归均方根值与故障类型和程度密切相关,以此为故障特征,建立BP 神经网络模型,对泄漏等故障的类型和程度进行诊断。文献[9]将改进的遗传算法和BP 神经网络相结合,提高BP 算法的收敛速度并用于电液伺服阀的故障诊断。 文献[10]建立调节阀正常状态下相关参数的CMAC 神经网络模型,计算模型输出与实际输出的残差,据此检测是否发生退化并确定退化的程度, 通过对5 种故障的检验验证了该方法的有效性和鲁棒性。
本文针对调节阀的故障信号特点, 利用非负矩阵分解方法提取信号的局部特征组成特征集, 由于该方法的鲁棒性, 可以在一定程度上排除外界干扰的影响, 故而利用特征集表示信号静态和动态的特点。 在此基础上,通过BP 神经网络实现对故障的诊断。 本文采用水箱实验平台的电动调节阀在5 类故障下的信号, 对文中方法进行了验证并与传统方法进行了对比。
1 故障诊断方法
1.1 非负矩阵分解
非负矩阵分解 (Non-negative matrix Factorization,简称NMF)方法的显著特点在于提取研究对象的局部特征, 其核心思想是在一般矩阵分解基础上加上非负性约束, 要求原始数据以及分解因子满足非负性,即被处理数据是分解矩阵的非负加和,该特点使维数灾难分解得到的两个低维矩阵具有天然的稀疏性和鲁棒性,可以抵御外界干扰,从而达到降维的目的[11-12]。
非负矩阵分解方法的求解属于一个NP 问题,文献[13]分别基于欧几里德距离的平方和广义KL 散度作损失函数, 通过交替优化的方式总结出了经典乘性迭代(Multiplicative Updates, 简称 MU)算法,自此得到了突破性的发展。
假设给定一个非负矩阵 X∈Rm×n,m 为变量个数,n 为样本个数,NMF 旨在将原矩阵分解为两个低维矩阵W 和H 的乘积:

式中:W 是 m×r 维的基矩阵;H 是 r×n 维的系数矩阵;r 的取值满足(m+n)<mn。 W 和 H 的求解属于一个最优化问题, 本文采用以欧式距离的平方为例的迭代算法进行优化计算,即以X 与WH 的误差最小作为目标函数:

式中:‖·‖表示范数。 乘法更新如下:

式(3),(4)中,算法的每一步都对 W 和 H 进行迭代,且由于X 的非负以及约束的非负, 使得每次迭代结果保证非负, 其最终的收敛性经由D.D.Lee 和H.S.Seung 得到证明,在此不再赘述。
1.2 BP神经网络
BP 神经网络是一种按误差反向传播训练的多层前馈网络,其算法称为BP 算法,它的基本思想是采用梯度下降法, 以期使网络的实际输出值和期望输出值的误差均方差为最小[14]。 其结构图如图1。
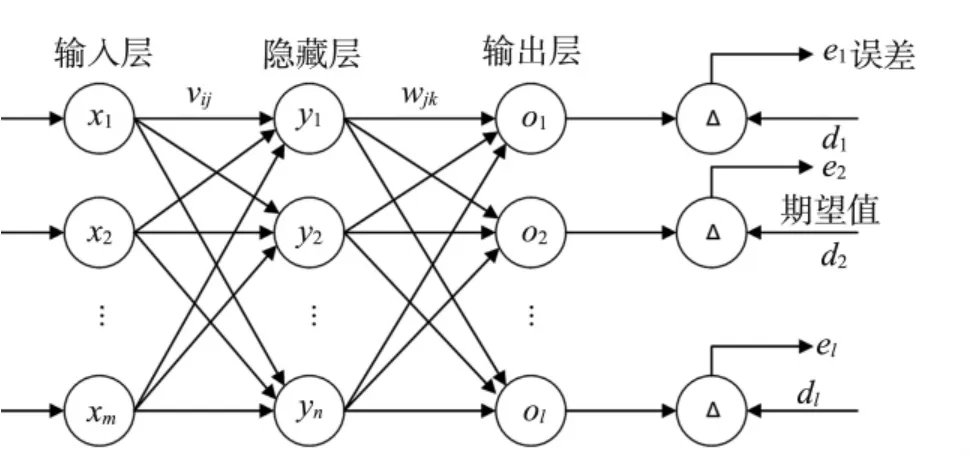
图1 BP 神经网络结构图
BP 神经网络由多个网络层构成,通常包括一个输入层、若干个中间层和一个输出层。 BP 网络的特点是:各层神经元仅与相邻层神经元之间有连接;各层内神经元之间没有任何连接; 各层神经元之间也没有反馈连接。 每一层的节点只与上一层和下一层的节点连接,而同层的节点之间没有连接,取出一个神经元结构可以得到图2 所示模型[15]。
如图2, 神经元是人工神经网络的基本处理单元,由3 种元素组成:
1)连接权值,是神经网络的重要特征,用以表征输入信号的特征。
2)加法器,用来求取输入信号的特征加权和。
3)传递函数,则是用于限制加权和的输出振幅,将输出信号限制在一定的范围内变化, 因此又被称作激活函数。
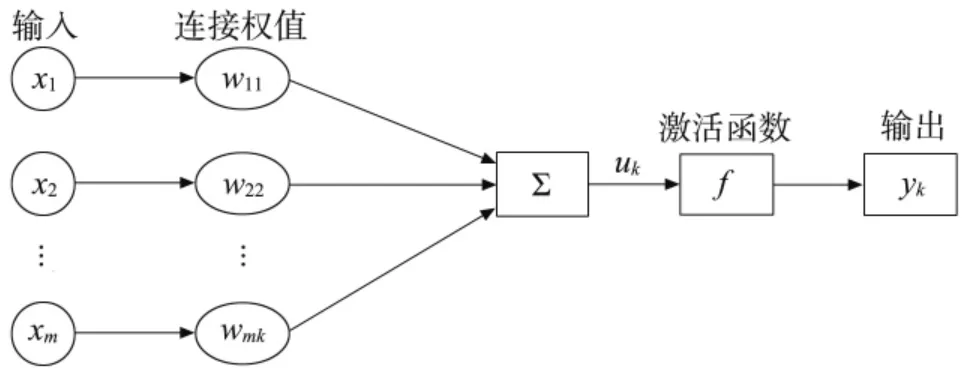
图2 神经元模型
结合本文针对调节阀的故障诊断研究内容,设计一个三层的BP 神经网络,其操作步骤如下:
步骤1,初始化网络参数。假设有n 个输入节点,m 个隐藏层输出节点,s 个网络输出节点,分别由xi,yj,ok(i=1,2,…,n;j=1,2,…m;k=1,2,…s)表示,vij表示输入层到隐藏层的权值矩阵,wjk表示隐藏层到输出层的权值矩阵。 激活函数选择sigmoid 函数f(u)=1 /(1+e-u)。
步骤2,分别计算隐藏层输出和网络输出,
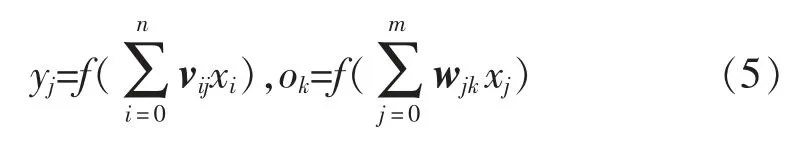
步骤3,根据实际输出与期望输出的误差,利用梯度下降算法,通过多次迭代迭代优化权值,直到满足收敛要求。
2 基于NMF特征提取的故障诊断步骤
非负矩阵分解具有优越的局部特征提取性能,在本文中采用分层分模块的方式提取, 可以保留原数据的静态和动态特性。而BP 神经网络具有优秀的学习能力,能有效学到数据内部的关系,但是依赖于输入数据的品质, 将两种方法结合, 形成基于NMF特征提取的故障诊断方法。 本方法的核心在于利用非负矩阵分解提取局部特征的优越性,配合BP 神经网络的学习与分类功能,实现故障诊断,具体步骤如下:
1)分别采集研究对象直接相关变量的正常及故障态数据,划分数据模块。
2) 使用非负矩阵分解提取各模块的局部特征,分别组成正常态特征集以及各类故障态特征集。
3)对所有特征集划分训练集与测试集,设置神经网络参数以及输出编码。
4)训练网络模型,并加以测试。
3 案例分析
调节阀在控制系统中举足轻重, 它接收来自控制器的指令信号,转化为实际动量操作,实现被控量的调节变化。 而一旦调节阀发生故障或劣化,必然影响调节效果, 难以达到或花费更大的成本达到预期目标。 对于一个系统,一旦调节阀出现故障,可能使机组效率降低甚至某些关键部位的调节阀会导致机组停运,造成巨大的经济损失。
对于调节阀故障,在艾默生水箱综合实验平台进行模拟。 该平台模仿生产实际,汇集温度、压力、流量等传感信号,可以实现单回路、串级、多入多出、耦合回路的实践。 本实验以双容水箱液位控制为例,通过外接OPC 通信服务,实现调节阀故障的模拟。 实验过程中,水箱系统运行的实时数据传输到上位机,上位机根据当前信号发出控制指令进入故障模块得到模拟的故障信号,再将该信号传输回实验平台驱动调节阀运作,以此实现故障的发生与检验。
以电动调节阀为例,实验中设置5 类故障模式,分别是恒增益故障、恒偏差故障、卡死故障、粘滞故障以及死区故障。 采集调节阀输入控制指令、调节阀阀位反馈指令、 调节阀流量信号作为分析故障的3 个变量,并就正常状态和5 类故障状态分别采集3 000 个数据点。为体现非负矩阵分解提取特征的性能,本文设置了对比实验,即使用特征集训练BP 神经网络和使用原始数据集训练BP 神经网络。
3.1 特征提取
对包含正常态在内的 6 个数据集 Xi∈R3×l,i=1,2,…,6,l=3 000,以 k 个数据点作为一个数据段(本实验中k 取100),则对每个数据集,其算法步骤如表1 所示。
经提取后得到由矩阵构成的6 个特征集Qi∈该特征集相比于原始数据矩阵以及传统的特征提取结果具有如下优点:

表1 算法步骤
1)特征集具有很强的可解释性。 特征集由每个数据段提取的基矩阵组成, 而每个基矩阵包含了该数据段的代表性信息, 可以用来表征一段时间内的运行状况。
2)特征集在一定程度上排除了外界干扰的影响,反映了运行状况的静态特征。每一个数据段因为相比整个数据集较小,其动态变化不明显,或基本保持稳定,或围绕中心作轻微波动。在特征提取过程中,数据段的本质信息被保留在基矩阵W 中, 而该数据段的波动变化则体现在系数矩阵H 中, 从而隔离了噪声干扰,基矩阵则体现了该数据段的静态特征。
3) 特征集整体上反映了原数据集的动态特征。单个基矩阵体现了一个数据段的静态特征, 而由多个数据段组合成的特征集则反映了在l/k 个过程中的变化特征,亦即动态变化。
4)特征集维数降低。经特征提取后,对每一个数据段, 由100 个样本提取出1 个代表该样本所有信息的特征样本,从而极大降低了数据维度。
3.2 BP神经网络训练与检测
为体现基于非负矩阵分解特征提取的优越性,使用BP 神经网络进行训练时, 分别采用特征集和原始数据集。 在训练中,设置网络输出的目标编码如表2 所示。

表2 神经网络输出编码形式
首先对特征集训练与检验, 每个样本经特征提取后得到长度为30 的特征样本, 取前20 个样本作为训练集,后10 个样本为测试集,设置BP 神经网络参数。同时使用原始数据对BP 神经网络进行训练和测试,对每一个故障样本,取前2 000 个数据点作为网络的输入,后1 000 个数据样本作为测试集,设置BP 神经网络参数如表3 所示。

表3 训练特征集和原始集的BP 神经网络参数对比
3.3 结果分析
分别使用非负矩阵分解提取特征后的特征集和原始数据集进行训练的神经网络对故障有不同的检测效果,具体结果如表4 所示。
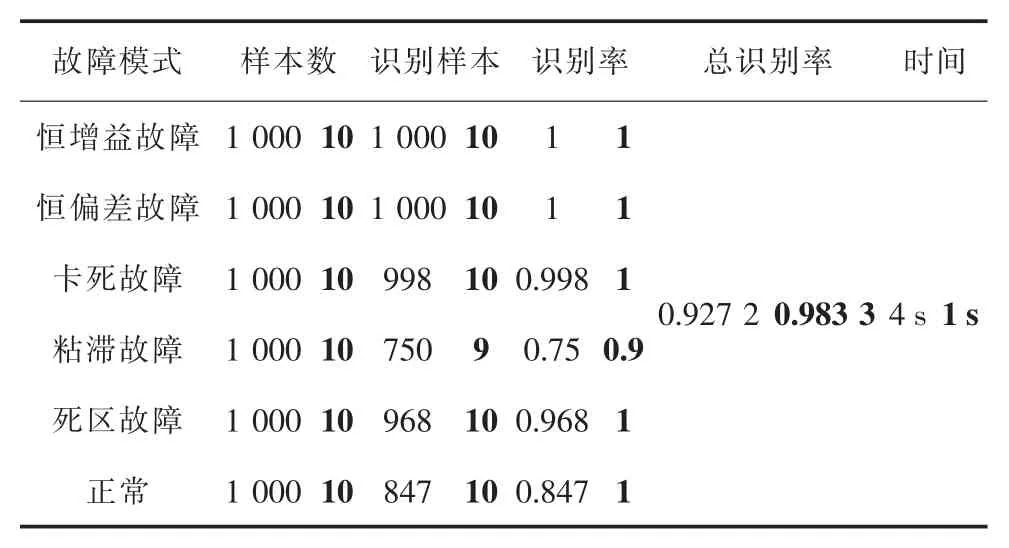
表4 使用原始数据和特征数据训练与测试的结果
表中数据分别包含使用原始数据的故障诊断结果(未加粗)以及采用非负矩阵分解提取特征后的诊断结果(加粗)。对比表4 中的结果,特征提取结果作为网络训练输入比使用原始数据具有更高的准确率,而且训练和检测所花费的时间更少。这说明非负矩阵提取的特征信息充分保留了原始数据的静态和动态特征,降低了数据维度,提高诊断效率。同时,分析使用原始数据诊断错误的样本发现, 对于粘滞故障样本, 发生识别错误的情况主要集中在变量数据上下波动时,经过正常态的阶段,在此刻内,虽然数据走势表现为正常, 但实际上只是波动过程的一个中间过渡状态,因而容易被神经网络误判为正常;对于正常样本,因为它的动态变化与死区样本接近,出现了类似粘滞误判的情况, 从而使神经网络诊断异常;相比而言,恒增益故障和恒偏差故障,它们各自的数据动态变化特征与其他故障具有明显的差异,所以诊断效率更高。 反观利用非负矩阵分解方法提取的特征集, 它表征了一段数据的总体动态和静态特性,不为局部数据点的变化所干扰,提高了诊断性能。
4 结束语
非负矩阵分解作为新的多元统计降维和特征提取方法,在提取局部特征、抵御外界干扰上具有显著的优势。 本文使用该方法提取电动调节阀的故障信号,实现降维的同时,充分保留了原数据的静态和动态特征,面对BP 神经网络的训练与检测,与直接使用原始数据比较, 具有更高的准确率以及更少的训练时间,充分证明本文方法的有效性。

