基于动态规划方法的变电站设备最优检修策略

张大宝，吴治勇

（国网新疆阿克苏供电公司，新疆 阿克苏 843000）

0 引言

变压器和断路器等电气设备在长期运行过程中，受电场、导体发热、机械力、化学腐蚀、环境因素等影响，可能会出现隐患，影响其工作可靠性，甚至缩短其寿命， 因此电气设备运行一段时间后需进行检修［1-2］。如果检修频率过高，可以提高设备的可靠性并减少设备故障的机率， 但寿命周期成本肯定会升高。如果检修频率过低，可以减少寿命周期成本，但降低了设备可靠性。

随着计算机、传感器和通信等技术的发展，电气设备状态在线监测技术不断成熟。 电气设备状态在线监测数据对于可靠性分析和检修具有很大的意义。已有的研究成果可以分为4 类：一是利用历史数据采用指数分布［3］和正态分布建立设备可靠性评价模型；二是阐述了检修模型的决策［4］；三是对寿命周期成本进行了研究和分类［5-6］；四是提出了利用不同算法求解非线性函数的方法。但是，以上方法没有同时考虑设备的全生命周期成本和可靠性， 检修策略具有片面性。 为此，本文提出了一种考虑全寿命周期成本（Life Cycle Cost，简称 LCC）和可靠性的变电站设备最优检修策略。

1 基于威布尔分布的设备可靠性评估

1.1 威布尔分布概述

威布尔分布是一种不确定性分布。 威布尔分布的概率密度函数是设备的有效寿命概率Tef， 如下式所示：

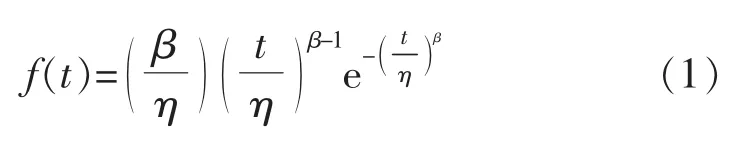
有两个参数描述了这种分布［7］。 第一个参数是形状参数β，它表示各设备的故障率特征，如早期故障率、使用寿命、磨损期等。 另一个参数是尺度参数η，它表示设备故障的平均时间。 利用最小二乘法对现有设备的故障记录数据进行分析， 找出形状参数和尺度参数［8］。

威布尔分布可用于设备的可靠性和故障率描述。

1）故障函数Q（t）表示设备在运行时发生故障的概率。 故障函数是累积分布函数，如下式所示：

2）可靠性函数R（t）表示设备正常运行的概率，其表达式如下：

3）故障率函数λ（t）表示老化对仪器可靠性影响，定义如下：

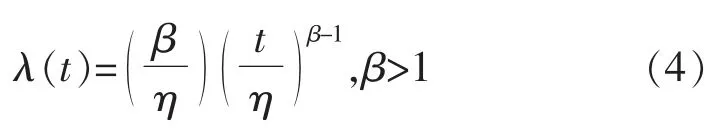
1.2 基于威布尔分布的设备状态检修

检修策略在不同可靠性情况下都会对设备的有效使用寿命产生影响。 由有效使用寿命和检修策略之间的关系， 可以构造出在时间T 内总共N个设备的检修计划。 对检修参数定义：i 为设备序号（i=1，2，…，N）；n 为时间段 T 上的间隔数；j 为阶段序号（j=1，2，…，n）；ti，j为第j 阶段第i 台设备的有效使用寿命；mi，j为第j 阶段第i 台设备的检修决策；ri，j为第j 阶段第i 台设备的更换决策。 决策变量（mi，j，ri，j）为 0 或 1。

检修决策与下一阶段的有效使用寿命有关，并对第j 阶段的第i 台设备采取行动。执行动作可以分为3 种类型：

1）无动作（mi，j=0，ri，j=0）。 此种情况下，下一阶段开始时的设备有效使用寿命等于上一阶段结束时的设备有效使用寿命加增加量，具体如下：

2）检修（mi，j=1，ri，j=0）。这个动作意味着对设备进行检修， 动作的结果降低了设备在下一阶段开始时的有效使用寿命，但是有效寿命并没有降低为0，或与前一阶段结束时相同，定义为：

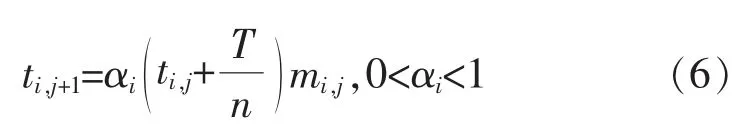
式中：α 是一个“改进因子”，在文献［9］中首次提出。如果α=0， 则设备的有效使用寿命返回到新设备状态。 如果α=1，即检修对设备状态没有影响。

3）更换（mi，j=0，ri，j=1）。这一动作意味着更换新的设备， 设备的有效使用寿命在下一阶段开始时降为零，表达如下：

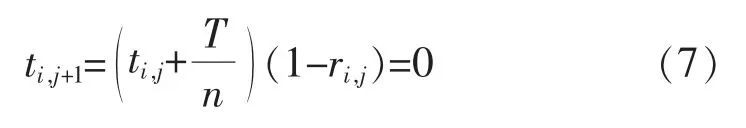
1.3 基于威布尔分布的LCC类型

在本文中LCC 可以分为两种类型。

1.3.1 纠正性检修费用

它又称为故障成本（CF），是由不可避免的或计划外的故障引起的。 这个费用取决于第i 个设备在第j 阶段发生故障的次数。

式 中：CFi，j为第i 台设备第j 阶段的故障成本 ；Fi为第i 台设备的单位故障成本；d 为通货膨胀率；Ni，j为第i 台设备第j 阶段的故障次数。

1.3.2 预防性检修费用

当对设备进行检修或更换时，计入该笔费用。 这个成本取决于每个设备的检修决策， 分为以下两种成本：

1）检修费用（CM）为设备实施检修策略时发生的检修费用，具体如下：

式中：CMi，j为第i 个设备在第j 阶段的检修费用；Mi为设备的单次检修成本。

2）重置成本（CR）为投入新设备的投资成本。 具体如下：

式中：CRi，j为第j 阶段第i 台设备的重置成本；Pi为设备的单次重置成本。

2 最优检修策略

为了使某一设备在要求的可靠性条件下LCC 值达到最小，提出了相应的检修策略。 目标函数CDi为：

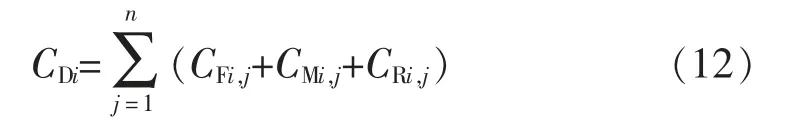
在满足约束条件下使CDi最小，约束条件：

式中：tDi，f为第i 台设备在第n 阶段的寿命限制。

设备有效使用寿命为：

决策约束为第j 阶段第i 台设备选择一个检修决策，即

可靠性约束为设备Ri，j的可靠性要求不低于规定值 RDr，req，即

动态规划法是由R.E.公司在20 世纪50 年代后期开发的［10］。 该方法能较好地解决决策和控制问题，特别是非线性优化问题。 采用动态规划法找到每个阶段的 LCC 最小值［11］，如图1 所示。

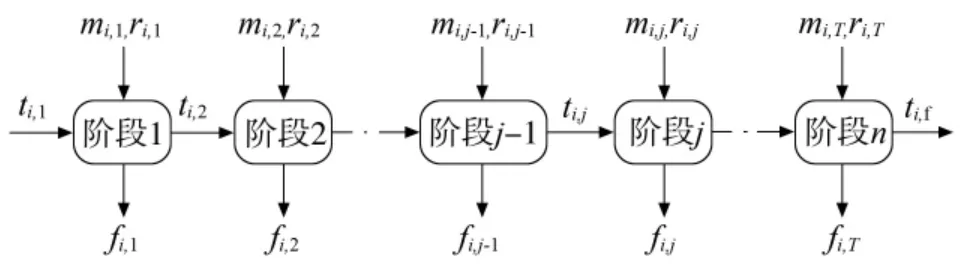
图1 动态规划原理图

图1 中 fi，j为动态规划中LCC 的值，其表达式为：

3 算例及分析

为了验证所提方法的有效性， 对有效寿命的历史数据进行威布尔分布建模，参数如表1 所示。

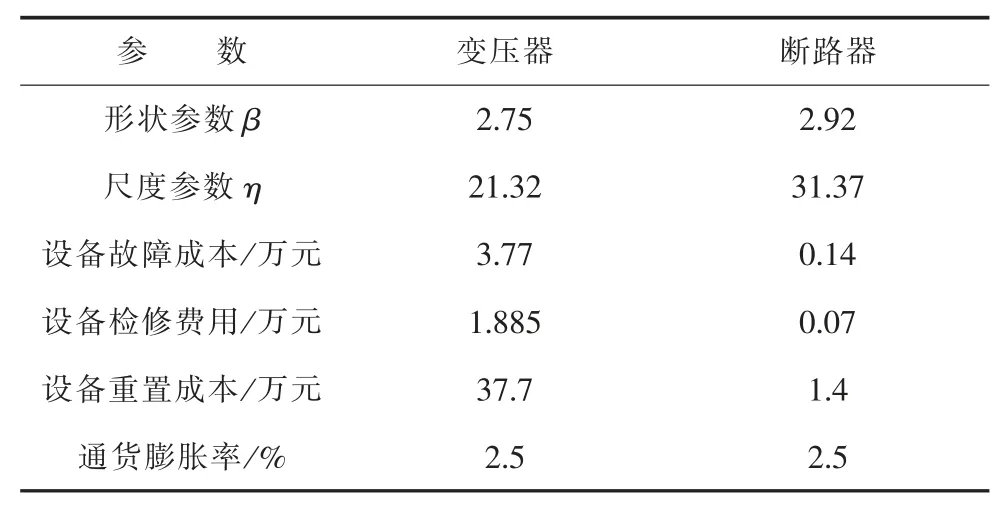
表1 威布尔分布及设备成本参数

3.1 设备检修策略及费用

检修变量定义为 α=0.5，n=20，T=20 a， 有效寿命边界条件如表2 所示。 末级设备可靠性大于0.9。为了在动态规划约束条件下使目标函数最小化，变压器和断路器的检修时间和LCC 的计算结果如表2 所示。 结果表明， 当有效寿命边界条件降低时，LCC 值和检修频率均有所增加。 此外，β 和η 都受到计划检修、可靠性和故障率的影响。 因此，不同设备的规划不同。

表2 采用动态规划法对变电站设备进行检修评估

变压器和断路器分别在寿命边界条件为9 a、8 a、7 a 以及平均年限下的可靠性如图2 和图3 所示。从图中可以看出，最优检修方案具有令人满意的可靠性。

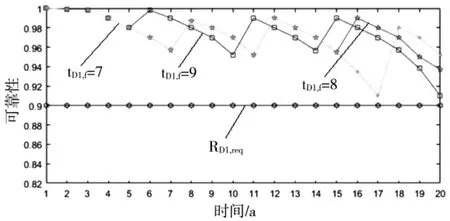
图2 变压器不同最终状态下的可靠性比较

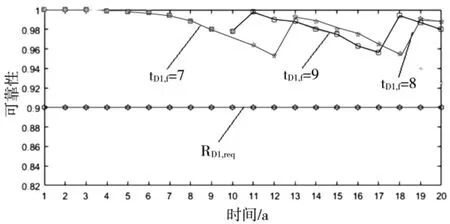
图3 断路器不同最终状态下的可靠性比较

3.2 与遗传算法的比较

遗传算法是一种利用生物学概念求解优化问题的组合优化方法，其优点是不用微积分法求最小值［12］。 在本算例中，遗传算法的参数选择：初始种群数为500，代数为6 000，交叉概率为0.1，变异概率为0.9。 采用遗传算法得出的变压器和断路器最终有效使用寿命下的LCC 计算结果如表3 所示。 实验结果表明，遗传算法没有得到最优解，而动态规化算法得到了最优解。 比较动态规化算法和遗传算法在2.40 GHz，Core-i5 的 CPU 上的计算时间， 动态规化算法的平均计算时间是30 min， 而遗传算法要超40 min才能得到答案。如果新一代和初始种群增加到6 000和500 以上， 遗传算法的计算结果更接近动态规化算法，但计算时间要长得多。对于具有初始条件和边界条件的问题，遗传算法并不能每次给出最优解。因此， 动态规化算法是求解组合优化问题的一种有效方法，其计算时间短，并总能得到最优解。

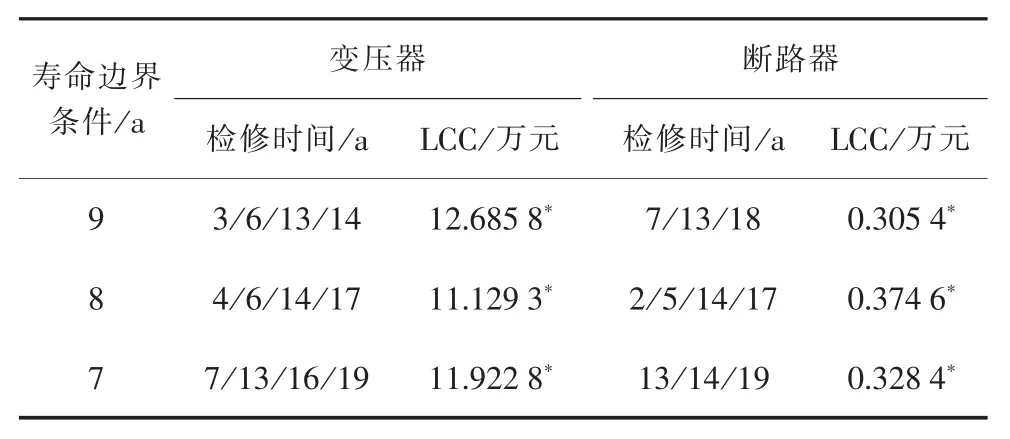
表3 采用遗传算法对变电站设备进行检修评估

4 结束语

本文提出了一种考虑设备全生命周期和可靠性的最优检修策略。 利用威布尔分布建立了设备概率模型，并将其应用于可靠性和故障率函数的求解。根据对设备使用寿命的影响，分为不同的策略类型。动态规化算法可以确定最佳的检修方案。 当有效寿命边界条件降低时，LCC 成本增加，检修频率增加。 不同使用寿命下的可靠性还受到设备形状参数和尺度参数的影响，从而能导致不同的检修方案。 此外，动态规化算法可以较容易得到最优解， 而遗传算法依赖于遗传参数和变量的数量， 有时会导致局部最小解。