基于SFA模型的奶牛不同养殖模式的技术效率研究——以内蒙古自治区为例

乌云花，王 慧，董晓霞

（1内蒙古农业大学经济管理学院，呼和浩特010010；2中国农业科学院农业信息研究所，北京100081）

我国奶牛养殖模式正在发生结构性变化，小规模养殖户所占的比例在逐渐下降，其他新型养殖模式不断出现［1］。散户和小规模养殖户逐步退出、规模养殖户在不断扩大，整个奶牛养殖业生产主体正在发生结构性转变［2］。我国奶业进入转变方式、调整结构、创新模式、强化管理、提高质量的新阶段［3］。

目前，学者们对不同养殖模式的效率及测定效率的方法进行了较为广泛的研究。郜亮亮等［4］在研究中指出，在其他因素不变的情况下，散养模式的技术效率低于中小规模养殖模式的技术效率，而且散户模式的产出效率也不如中小规模养殖的稳定。Wu等［5］指出，在养殖模式前端主要包括散户养殖、养殖小区及牧场等三种养殖模式，相对来讲养殖小区模式在降低成本提高收益方面有一定的优势。杜凤莲等［6］在研究中指出，散养、养殖小区和牧场三种模式的经济效率都不高，最低的为散养45.9%，最高的为牧场62.3%。曹暕等［7］也在研究中指出我国农户奶牛养殖平均技术效率为70%。李冬雪等［8］研究黑龙江奶牛场的管理效率中指出，黑龙江省的大规模奶牛场的管理效率平均值为0.715。马恒运等［9］的计算结果是中国牛奶生产的技术效率水平大约为80%—90%。彭秀芬［10］研究得出2004—2006年我国原料奶生产的平均技术效率为91.1%。而刘威等［11］的研究结论表明我国牛奶生产的平均技术效率值仅为78.3%。

不管是研究不同养殖模式的效率还是研究测定效率的方法，学者们的研究结论有很大的差异。大部分研究在样本和变量选择上有所不同，而且最大区别在于模型的选择上，不同生产效率模型会导致不同的研究结论，现有的大部分研究在选择模型的时候缺乏一定的定量检验。本研究运用随机前沿分析（SFA）模型在内蒙古呼和浩特周边地区利用最新的第一手调研数据，对养殖牧场、养殖小区及散户养殖等不同养殖模式的技术效率进行计算与比较，并探讨技术效率损失的影响因素。

1 研究方法

首先检验模型设定，然后利用SFA模型计算奶牛不同养殖模式的技术效率，并探讨其影响因素。SFA模型一般形式为：

式（1）中，Pi表示第i个单位的产出量；xi表示第i个单位的投入量；α为模型的待估系数。vi是模型的随机误差项，假设vi服从正态分布，均值是0，方差是σ2v，vi～N（0，σ2v）；μi表示由技术无效率引起的随机误差，反映第i个单位的技术效率损失的随机变量，其值大于或等于零。通常假定μi服从均值为b，方差为 σ2μ的半正态分布［12］，μi～N（b，σ2μ）；νi与 μi相互独立。

将SFA技术效率定义为：

式（2）中，te是实际产出水平与没有技术效率损失的产出水平之比，如果没有效率损失，te为1，一般情况下te小于1。te越大说明效率损失越小；反之亦然［12］。

令［13］：

其中，γ的取值为0—1。γ值的检验能反映出生产单位的技术效率的变异是不是具有统计显著性，如果接受γ＝0的假设，也就是σ2μ＝0，这样实际产出值与最大的产出值之间的差异主要来源于随机误差项ν，说明不存在技术效率损失，μ从模型中去掉，采用普通最小二乘法估计；若接受γ＝1的假设，则表明SFA的误差部分主要来源于技术效率的损失［12］。

模型设定首先采用常用的超对数生产函数形式，用最大似然比（LR）检验法来验证函数形式是否适用。超对数生产函数为［12］：

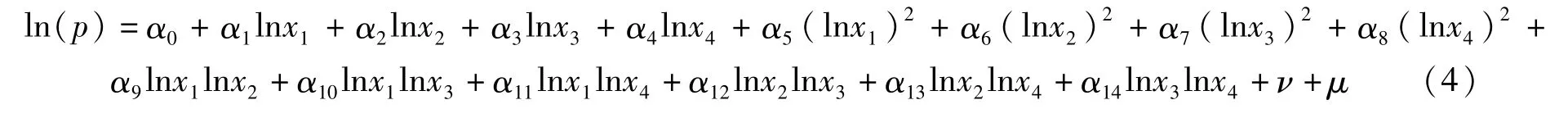
其中，p表示原料奶年产量（单位：kg），x1为劳动力投入天数（d），x2为固定资产投入［元（人民币，下同）］，x3为精饲料投入（kg），x4为粗饲料投入（元）。当上面式中所有平方项和交差项系数均为零时，超对数生产函数就会变为Cobb-Douglas生产函数。

考虑技术效率的影响因素时，由于调研区域的社会经济条件、环境气候、奶牛的品种等方面基本差不多，因此只考虑养殖规模、不同模式、养殖户的个人特征及精粗饲料配比等影响因素。

技术效率函数的具体形式为：

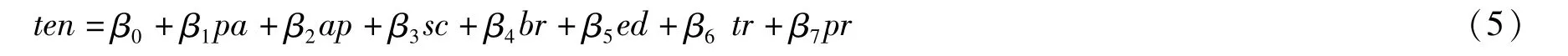
其中，ten表示技术无效率的程度，pa为养殖牧场的虚变量（是牧场模式＝1，其他＝0），ap为小区模式的虚变量（是小区模式＝1，其他＝0），sc表示养殖规模（头），br是养殖年限（年），ed是养殖户的受教育程度（年），tr是养殖户是否接受过培训（是＝1，否＝0），pr是精饲料和粗饲料的比例（%）。

2 数据来源

调研区域选择在奶牛养殖模式比较多样的呼和浩特周边地区，根据奶牛养殖头数，在每个区域分别选择了3个县，每个县选择两个镇（每个镇选择一个牧场），每个镇选择两个村（每个村选择一个养殖小区），每个村随机选择10个奶牛养殖户。由于近年来养殖户退出的比较多，最后收集到36个养殖户，46个牧场及19个养殖小区的相关数据。

3 不同养殖模式效率差异的理论逻辑

从产业经济学理论可知，某个产业的特点决定该产业的组织模式和组织结构，影响其规模化程度，最终影响其生产效率［14］。从奶业经济的鲜活性、交易的弱质性、信息不对称性、自然风险和市场风险大等特点看，规模养殖比散户养殖具有一定的优势［4］。但是，从整体产业的发展看，不同主体如果按一定的比例形成的规模结构会更有利于整个产业实现生产的协同效应［11］。从奶业养殖规模来看，规模过大的牧场生产成本远远高于规模小的牧场，造成整个奶牛产业的效率损失，使整个奶牛产业很难实现规模效益。另外，奶产业存在很高的退出壁垒，导致资源要素无法合理流动，最终造成低效率。因此，预期目前规模牧场的效率不一定与其他养殖模式的效率有很大的差别，需要进一步验证。

4 实证模型结果

4.1 检验函数设定

首先验证生产函数的形式是否适当，用LR检验法对超对数生产函数和Cobb-Douglas生产函数进行检验，检验统计量为［12］：

其中，l（θ1）是无约束条件下 θ的最大似然估计值，l（θ0）是有约束条件下 θ的最大似然估计值［12］，p为条件个数。

表1中，假设1是Cobb-Douglas生产函数，假设2不存在技术效率损失。检验结果显示，超对数函数比Cobb-Douglas生产函数优越［12］，函数设定是适当的。

表1 函数设定检验结果Table 1 Testing results of themodel specification

4.2 模型估计结果

超对数生产函数模型估计结果见表2。首先，γ为正，且在1%的水平上显著，说明不同养殖主体在奶牛养殖过程中存在显著的效率损失。其次，固定资产投入对牛奶产量有正的极显著的作用，在统计上达到1%的极显著水平。在调研中也发现，在3种养殖模式中，很多散户的设施简陋粗糙，设施不健全，在固定资产投入上远远不如牧场和养殖小区，所以散户的奶牛平均单产水平低于其他模式。再次，精饲料投入对牛奶产量的贡献显示了U型作用。精饲料投入一次项的系数估计符号为负，但没有通过显著性检验。而精饲料的二次项对产量起到5%的正向显著作用。最后，对产量有统计显著作用的还有各种投入的交叉项。交差项系数为负数说明一种投入的增加会引起另一投入的减少。比如，固定资产与劳动力投入的交叉项系数达到5%的统计负显著水平。劳动力与精饲料投入及固定资产与精饲料投入交差项为正，都达到5%的统计显著水平。

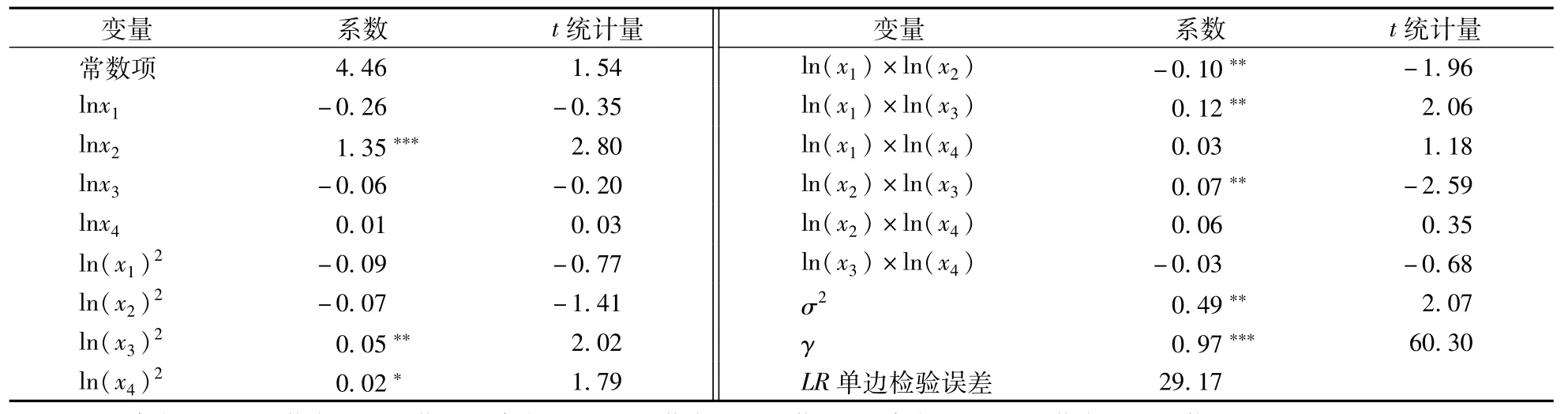
表2 SFA的估计结果Table 2 Results of the SFA

4.3 投入产出弹性

投入要素的产出弹性也可以说明各投入要素对养殖技术效率的影响。公式为：

其中，εx1、εx2、εx3和εx4分别表示劳动力、固定资产、精饲料和粗饲料投入的产出弹性。α值来源于表2的估计结果，lnx1、lnx2、lnx3、lnx4取各投入要素的几何平均值，结果见表 3［12］。

表3 投入要素的产出弹性Table 3 Output elasticity of input factors

从表3可知，除了劳动力产出弹性，其他产出弹性都是正值。劳动力的产出弹性是负的表明可能存在劳动力投入过剩的问题，如果增加劳动力的投入对牛奶产出没有积极的作用［12］。这一结论与其他学者的研究（例如曹暕等［7］）相吻合。固定资产的产出弹性为正值，说明继续增加固定资产的投入可以提高产奶量。精饲料和粗饲料投入的产出弹性也是正值，继续增加精饲料和粗饲料的投入量也有利于提高产奶量［12］。对比来讲，固定资产的产出弹性相对大，说明固定资产的投入对产出的贡献比其他投入要更大。

4.4 不同养殖模式技术效率的测算

牧场模式的技术效率平均值达到0.88，养殖小区模式的技术效率平均值为0.84，散户模式的技术效率平均值为0.73（表4）。如果按照效率分组，效率值大于90%的区域里牧场比例是39%，养殖小区的比例是42%，而散户的比例只有14%（表4）。不同养殖模式的技术效率都有一定的提升空间。

表4 不同养殖模式的技术效率对比Table 4 The com parison of technical efficiency of different breeding patterns

4.5 效率损失的决定因素的估计结果

首先，相对比小规模养殖散户模式，牧场和养殖小区模式对技术效率损失有负的显著影响。即，牧场和养殖小区的技术效率高于散户的技术效率，在统计上分别达到5%和1%的显著水平（表5）。因此，养殖模式显著影响技术效率。其次，养殖年限对技术效率损失产生了显著的正向影响。即：养殖年限越长，技术效率损失越大。这可能是由于养殖年限长意味着养殖户年龄大，年龄越大，新技术的接受能力越低，对技术效率的提高是不利的。再次，精粗饲料比值对技术效率损失有显著的正向影响。即：精粗饲料比值越高，技术效率损失越大（表5）。这表明精饲料和粗饲料配比存在问题，如果减少精饲料的投入，适当增加粗饲料的投入，可以提高技术效率。最后，养殖头数对技术效率损失的影响是负显著的。即：养殖规模越大，技术效率损失就越小（表5）。这在一定程度上说明了奶牛养殖业仍存在规模效应，目前的养殖规模还没有达到最优规模。适当的规模经营对技术效率的提高有显著的推动作用。

表5 技术效率损失决定因素的估计结果Table 5 Results of the determ inants of technical efficiency loss

5 结论与政策建议

本研究以内蒙古呼和浩特周边地区为例，对3种奶牛养殖模式包括牧场、养殖小区及散户的技术效率及影响因素进行了实证研究，得出如下的几点研究结论：首先，模型设定检验表明超对数函数比Cobb-Douglas生产函数优越，模型设定是适当的。其次，超对数生产函数模型结果表明，各种投入因素里固定资产投入对牛奶产量的提高有极显著的正向影响，说明可以继续适当增加固定资产的投入对牛奶产量的提高有积极作用。再次，投入要素的产出弹性估计结果表明劳动力的产出弹性是负值，说明可能存在劳动力投入过剩的现象。其他投入量的产出弹性都是正值，其中固定资产的产出弹性最大，说明固定资产投入对产出的贡献比其他投入更大。最后，技术效率损失的影响因素模型估计结果表明，养殖模式和养殖规模对技术效率的提高有显著的正向影响，精粗饲料比和养殖年限对技术效率的提高有显著的负向影响。

以上研究结论有重要的政策含义。首先，从不同养殖模式的技术效率都没有达到理想水平来看，我国的奶牛养殖业的发展任重道远，应该引起各方的足够重视。其次，规模养殖虽然在技术效率上体现出具有一定的优势，但是如果盲目扩大养殖规模，不仅养殖成本无法控制，对环境也会造成很大压力。调研中也发现，一些牧场为获得政府补贴追求数量和规模的盲目扩张，对草地、耕地等有限自然资源过度需求，导致资源要素无法合理流动，因此规模发展决不能贪大求快。最后，科学的精粗饲料配比对提高牛奶产量至关重要。从精粗饲料比对牛奶产量有显著的负向影响看，需要适当减少精饲料投入，提高粗饲料营养和数量。饲料资源的丰富与否是奶牛养殖是否可以持续发展的重要条件。调查过程中发现很多养殖户过度强调精饲料的作用，而忽视了粗饲料的作用，精饲料在投入上存在一定的浪费。