高冲击载荷作用下弹载记录仪防护系统动力学响应特性*

程祥利，赵 慧，焦 敏，叶海福，李林川

（中国工程物理研究院电子工程研究所，四川 绵阳 621999）

侵彻武器系统研制过程中，通常利用弹载记录仪采集侵彻硬目标过程中的过载信号[1-5]，为侵彻战斗部结构设计、装药安定性设计、侵彻引信抗高过载设计提供优化依据。由于弹载记录仪在侵彻过程中要承受峰值很高的高冲击载荷，需要进行有效的防护设计才能确保弹载记录仪内部电路的生存性及工作可靠性。

传统的防护设计方法以应力波衰减理论为基础[6-7]。当峰值很高的应力波从波阻抗很高的材料向波阻抗很低的材料传递时，幅值会大幅降低。在该理论指导下，起支撑作用的壳体材料的波阻抗越高越好，如选用高强度合金钢[8]，起防护作用的缓冲材料波阻抗越低越好，如选用聚四氟乙烯、橡胶、发泡聚氨酯等软质材料[9]，并通过了典型试验工况的考核。

但是，基于应力波衰减理论去揭示防护系统的动力学响应机理时存在比较明显的缺陷，既无法分析高冲击载荷加载频率(或脉宽)的影响，也无法分析防护系统其余参数的影响，如防护对象质量、缓冲材料厚度等，而这都是影响防护系统动力学响应特性的关键因素。因此，需要探索或引入新的分析方法以全面、有效地揭示防护系统的动力学响应机理。

为此，从机械振动的角度出发，通过建立一种简化的动力学响应模型来揭示高冲击载荷作用下弹载记录仪防护系统的动力学响应机理。首先，分析弹载记录仪内部的载荷传递关系，将缓冲材料等效为具有阻尼特性的线性弹簧，基于双自由度弹簧-质量-阻尼系统建立防护系统的动力学响应模型；随后，以某种防护结构为研究对象，建立有限元模型，通过脉冲响应分析和谐响应分析获得系统的固有频率和阻尼比，并验证动力学响应模型的准确性；最后，借助幅频响应特性分析不同参数对动力学响应特性的影响规律，以期为弹载记录仪防护系统设计提供依据。

1 防护设计

弹载记录仪内含高g值加速度传感器和各种处理电路，用于采集侵彻过程中的加速度信号。为了提高弹载记录仪的抗冲击能力，从两方面开展防护设计，原理如图1 所示。首先是灌封加固[10-11]，选用环氧树脂作为灌封材料将电路部分灌封成一个组件，目的是提升电路自身的抗冲击能力；其次是缓冲隔离，选用硅橡胶作为缓冲材料填充在灌封成型的电路组件与机械壳体之间，目的是通过缓冲材料的低波阻抗特性来衰减高频应力波，以减小传递至电路组件的作用力。

图1 防护设计Fig.1 Protection design

防护设计完成后，便可得到简化的弹载记录仪内部的载荷传递关系，如图2 所示。外部高冲击载荷首先作用于弹载记录仪的机械壳体，并通过缓冲材料传递至灌封成型的电路组件，再通过组件内部的灌封材料传递至电路板，进而影响安装在电路板上的各种元器件的生存性及工作可靠性。

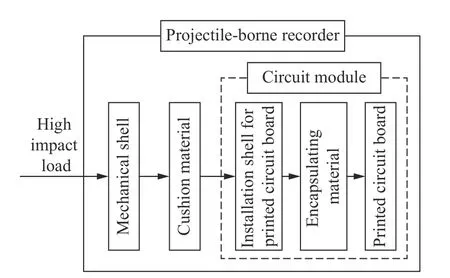
图2 载荷传递关系Fig.2 Schematic diagram of load transfer

2 动力学响应模型

2.1 动力学微分方程

弹载记录仪设计时，机械壳体选用高强度金属，弹性模量为上百吉帕；电路组件内部灌封有环氧树脂，弹性模量为几吉帕；电路组件与机械壳体之间填充有硅橡胶类缓冲材料，弹性模量仅为几十或几百兆帕。由于弹性模量的差异，高冲击载荷作用下缓冲材料的变形远大于机械壳体与灌封材料的变形，导致电路组件整体剧烈振动。因此，可从机械振动的角度揭示防护系统的动力学响应机理。

假设机械壳体与灌封材料的变形可忽略，则灌封成型的电路组件可等效为一个整体，机械壳体可等效为基座。假设缓冲材料的变形在弹性范围内，则缓冲材料可等效为具有阻尼特性的线性弹簧。此时，弹载记录仪防护系统的动力学响应模型可简化为双自由度弹簧-质量-阻尼系统[12]，如图3 所示，两个自由度分别代表电路组件和机械壳体的运动。图3 中：m为电路组件的质量，M为机械壳体的质量；k为等效刚度，代表缓冲材料的弹簧支撑作用；c为等效阻尼，代表缓冲材料的能量耗散作用；xm、xM分别为电路组件、机械壳体相对于初始位置的位移，两者的差代表缓冲材料的变形量；aM为外部高冲击载荷。

图3 双自由度弹簧-质量-阻尼系统Fig.3 A two-degree-of-freedom spring-mass-damper system

对电路组件和机械壳体分别进行受力分析可知，电路组件仅受缓冲材料弹性变形引起的弹簧力和阻尼力，机械壳体除受缓冲材料弹性变形引起的弹簧力和阻尼力外，还受高冲击载荷作用，即MaM。根据牛顿第二定律可得双自由度系统的动力学微分方程：

2.2 传递函数

对式(1)进行拉普拉斯变换，即用s代替d/dt，可得动力学微分方程在复数域内的表达式：

对式(2)化简，并消除中间变量XM(s)，可得到以外部高冲击载荷AM(s)为输入、以电路组件位移Xm(s)为输出的传递函数：

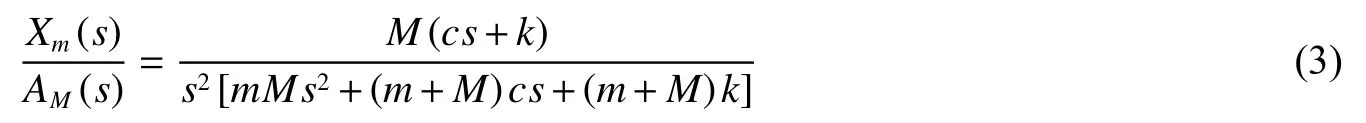
根据加速度与位移的二阶导数关系(即am=d2xm/dt2)，可得到以外部高冲击载荷AM(s)为输入、以电路组件过载Am(s)为输出的传递函数：

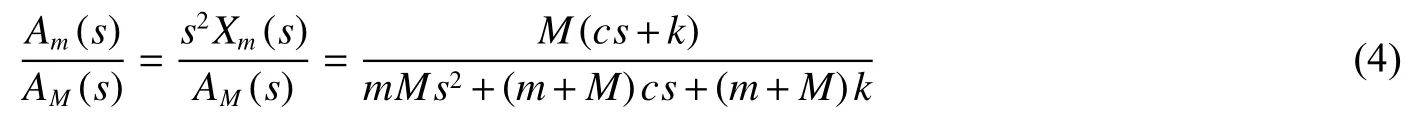
即弹载记录仪防护系统的动力学响应模型，属于典型的二阶系统[13]。

由于弹载记录仪通过螺纹与侵彻战斗部固连，因此机械壳体质量M包含战斗部质量，可近似认为机械壳体质量远大于电路组件质量，即M>>m，此时，式(4)可简化为：

式中：ωn为防护系统的固有频率，单位为rad/s；ξ 为防护系统的无量纲阻尼比。

3 分析与讨论

为了验证动力学响应模型的准确性，以某种防护系统为研究对象，利用ANSYS/LS-DYNA 软件开展了数值模拟。建立的有限元模型如图4 所示，包括安装基座(模拟质量远大于电路组件质量的侵彻战斗部)、机械壳体、缓冲材料、电路组件，详细的材料参数如表1 所示。

图4 有限元模型Fig.4 Finite element model

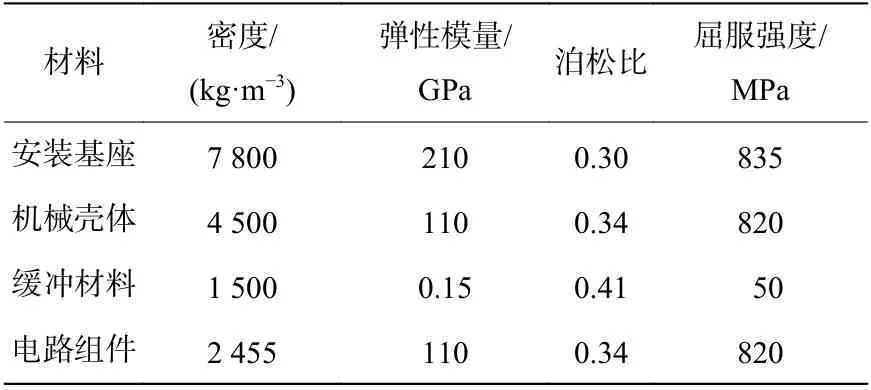
表1 材料参数Table 1 Material parameters

3.1 脉冲响应分析

脉冲响应分析反映了系统的固有特性[14]，因此，以持续时间很短的脉冲信号(峰值10 000g，持续时间0.005 ms)作为模拟输入，如图5 所示，并施加在安装基座的下底面。

图5 脉冲输入信号Fig.5 Impulse input signal

模拟完成后，提取电路组件的过载变化曲线，如图6 所示。可以看出，防护系统表现出明显的周期振荡衰减特性。其中，振动周期由固有频率决定，衰减特性由阻尼比决定。

图6 中，点(t1,A1)、点(t2,A2)为完全进入自由振动阶段后的两相邻峰值点。根据系统特性与固有频率、阻尼比的关系[12]，可得到防护系统的固有频率约为5.6 kHz，阻尼比约为0.06，过程如下：

固有频率与阻尼比已知后，可得到防护系统的传递函数模型：

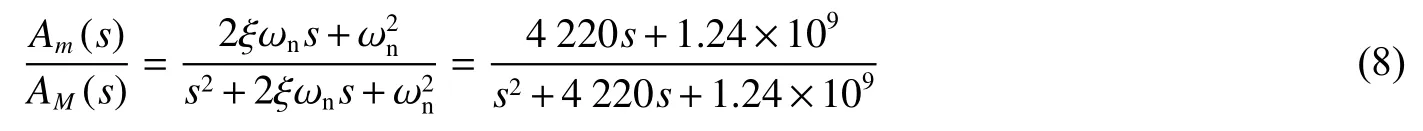
传递函数已知后，采用数值积分的方法进行了理论计算，预测同一脉冲信号作用下的防护系统动力学响应特性，并和有限元模拟结果对比，以验证动力学响应模型的准确性。理论计算结果与有限元模拟结果的对比如图7 所示。

为了验证动力学响应模型的准确性，用相关系数[15]评价理论计算结果与有限元模拟结果的相似程度：

式中：Y1、Y2为两组数据，分别代表理论计算结果和有限元模拟结果；r(Y1,Y2)代表两组数据的相关系数，Cov (Y1,Y2)代表两组数据的协方差，Var (Y1)、Var (Y2)代表每组数据的方差。

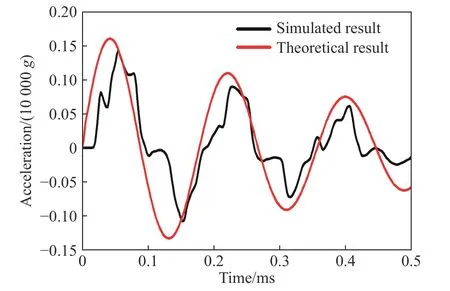
图7 理论计算结果与有限元模拟结果的对比Fig.7 Comparison between theoretical and simulated results

相关系数越接近1，两组数据的相似程度越高。本文中，理论计算结果与有限元模拟结果的相关系数为0.81，说明本文简化的防护系统动力学响应模型是基本符合实际情况的，能较准确地描述防护系统在高冲击载荷作用下的动力学响应特性。

3.2 谐响应分析

谐响应分析反映了系统在正弦加载时的稳态特性[16]，而侵彻过程中，任何结构和材料都会出现不同程度的变形，而且拉伸变形与压缩变形交替[17-19]，说明电路组件承受的载荷可近似为正弦信号。因此，以不同频率的正弦信号(峰值10 000g)作为模拟输入，如图8 所示，并施加在安装基座的下底面。

图8 正弦输入信号Fig.8 Sinusoidal input signal

模拟完成后，提取电路组件的过载变化曲线，如图9 所示。可以看出，正弦加载条件下，电路组件经防护系统后的响应近似为同频率的正弦信号，只是系统达到稳态后的峰值不同，即同一系统在不同的加载频率下表现出明显不同的响应特性。对于本系统，在加载频率为5.4 kHz时，防护系统表现出明显的振动放大效应。

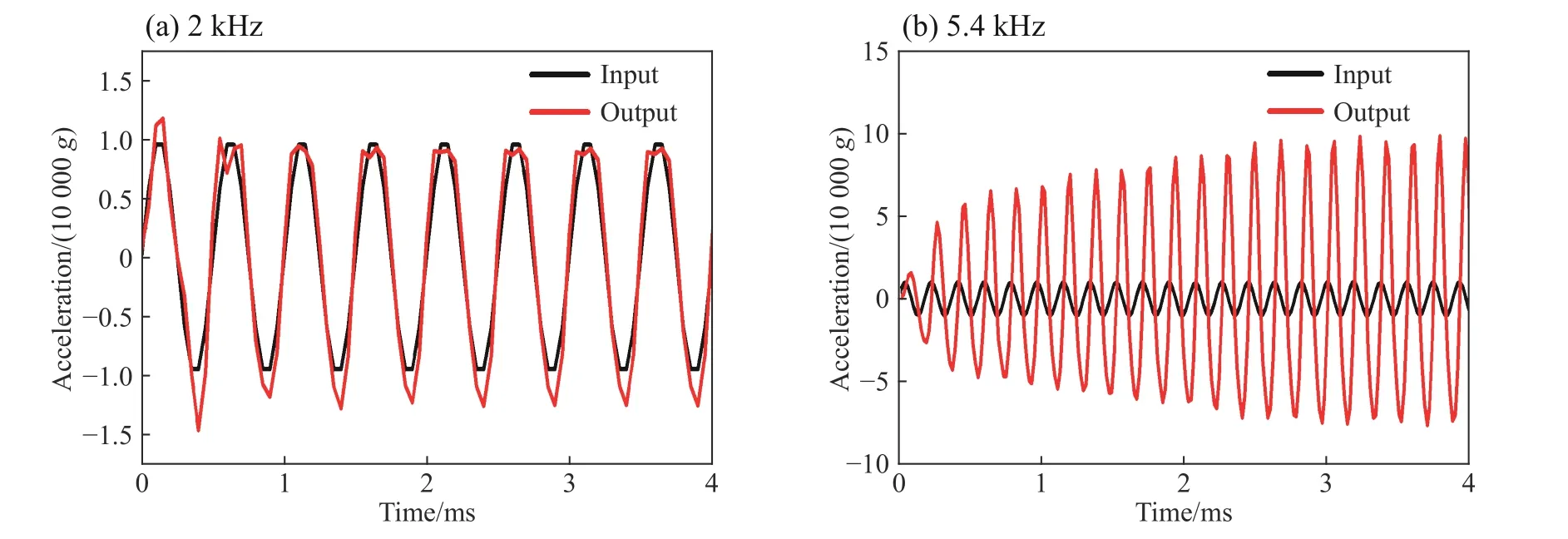
图9 不同频率正弦信号输入的模拟结果Fig.9 Simulated results of sinusoidal signals with different frequencies

提取系统达到稳态响应时的电路组件过载峰值，并分析其随正弦信号频率的变化规律，如图10 所示。可以看出，加载频率为5.4 kHz 时，防护系统开始共振，峰值约是外部加载信号峰值的10 倍，说明该系统的固有频率约为5.4 kHz，阻尼比约为0.05，与前述的脉冲响应分析结果吻合，再次验证了动力学响应模型的准确性。

图10 稳态幅值随正弦信号频率的变化规律Fig.10 Steady amplitude curve of sinusoidal signals at different frequencies

为了揭示加载频率对防护系统动力学响应特性的影响规律，对系统进行频域分析，用自动控制理论中的幅频响应特性[13]描述防护系统的动力学模型。令s=jω，代入式(5)，并取模可得动力学响应模型的幅频响应特性，即加速度传递系数：

式(10)反映了正弦加载条件下系统达到稳态时输出幅值与输入幅值之间的关系。其中，j 为复数单位，ω 代表外部高冲击载荷的加载频率。

由式(10)可知，加速度传递系数仅与阻尼比、频率比(加载频率与固有频率的比值)有关。因此，本文中主要分析固有频率、阻尼比对动力学响应特性的影响规律。

为了分析方便，记稳态幅值为20 lg︱Am(jω)/AM(jω)︱，单位为dB。此时，幅频响应特性随固有频率的变化规律如图11 所示。图11 中包含两种防护系统，其固有频率不同(ωn1＜ωn2)，阻尼比均为0.05。可以看出：(1)系统响应存在放大区和衰减区。传递系数大于0 dB 说明防护系统会将外部的高冲击载荷放大，特别是当频率比靠近1 时，传递系数会大幅增大，即共振。当频率比较大时，系统才会表现出明显的衰减效应。(2)同一防护系统在不同的加载频率下会有不同的响应特性，趋势甚至会相反。当频率比小于1 时，曲线单调递增；当频率比大于1 时，曲线单调递减。(3)不同防护系统在同一加载频率下会有不同的响应特性。当频率比小于1 时，传递系数随固有频率的增高而减小，当频率比大于1 时，传递系数随固有频率的增高而增大。

图11 不同固有频率时的幅频响应特性Fig.11 Amplitude-frequency response characteristics at different natural frequencies

因此，可根据高冲击载荷的加载频率与防护系统固有频率之间的匹配关系指导弹载记录仪的防护设计。当加载频率低于固有频率时，适当提高防护系统的固有频率有助于降低传递至内部电路组件的过载。提高固有频率的方法主要有增强支撑刚度、减小电路组件质量。而对于加载频率高于固有频率的情况，结论是相反的。

幅频响应特性随阻尼比的变化规律如图12 所示。可以看出，阻尼比主要影响发生共振时(频率比靠近1)的幅频响应曲线的峰值，随着阻尼比的增大，传递系数峰值大幅减小，说明提升缓冲材料的能量耗散能力有助于减小传递至内部电路组件的作用力。

图12 不同阻尼比时的幅频响应特性Fig.12 Amplitude-frequency response characteristics at different damping ratios

4 结 论

采用理论分析与数值模拟相结合的方法研究了高冲击载荷作用下弹载记录仪防护系统的动力学响应特性。基于双自由度弹簧-质量-阻尼系统建立了简化的防护系统动力学响应模型，并得到了数值模拟结果的验证，从中可以得到以下结论：

（1）简化的双自由度弹簧-质量-阻尼系统能较准确地预测弹载记录仪防护系统在高冲击载荷作用下的动力学响应特性。

（2）高冲击载荷的加载频率与防护系统固有频率之间的关系决定了系统的动力学响应特性。加载频率低于固有频率时，传递系数随固有频率的增高而减小；加载频率高于固有频率时，传递系数随固有频率的增高而增大。

（3）设计弹载记录仪防护系统时，要密切关注外部高冲击载荷的频率成分。当高冲击载荷的频率成分主要集中于低频段时，适当提高防护系统的固有频率是有利的，对应的措施是减小电路组件质量、适当增强支撑刚度。