基于KPCA-SVM模型的电力负荷最大值短期预测方法

张永伟，潘巧波

基于KPCA-SVM模型的电力负荷最大值短期预测方法

张永伟1，潘巧波2

（1．安徽邮电职业技术学院通信工程系，安徽省 合肥市 230000；2．华电电力科学研究院有限公司，浙江省 杭州市 310030）

电力负荷最大值预测是电网企业调度工作的重要组成部分，其预测结果的准确度将对电能的配送、有效利用率、供电服务的质量以及电力系统的发展产生重要影响。以安徽某市81天的电力负荷最大值数据为基础，选取影响当天电力负荷最大值的10个因素，并采用核主成分分析(kernel principal component analysis，KPCA)算法将10维的影响因素降为5维，其累计贡献率可达93.70%。以降维后的5维数据为输入，以径向基函数为核函数，并采用交叉验证选择支持向量机(support vector machine，SVM)回归的最佳参数，随机选取54组数据训练SVM预测模型，最后进行27组数据的拟合预测，拟合预测的均方误差为0.0041，相关系数为0.9631。研究结果表明，应用KPCA结合的SVM预测模型对电力负荷最大值具有很好的预测能力。

电力系统；负荷；核主成分分析(KPCA)；支持向量机(SVM)；预测模型

0 引言

电力系统负荷最大值的有效预测直接影响到电力调度是否高效，电力能否得到合理分配与利用[1]。当电力负荷最大值预测偏高时，会导致当前电力设备闲置，得不到充分利用，从而造成超前投资和资源浪费；当电力负荷最大值预测偏低时，就会造成电网的电能供应能力不足，用户正常的电力需求不会得到满足，并存在整个供电系统崩溃的风险。因此，电力规划和调度部门应具备电力负荷最大值预测的基本数据信息，从而制定调度合理、分配高效、节省能源、持续可靠的科学决策和方案[2-3]。

针对电力负荷最大值的预测问题，目前研究主要集中于短期负荷最大值预测和中长期负荷最大值预测方面[4]。对于短期电力负荷最大值预测，通过预测未来7~10天的用电量，让发电企业制定对应的发电策略，以此能够对市场的需求做出及时的反应[5]。要保障每日电力负荷最大值预测的准确率，选择适当的预测算法是十分关键的。

传统的预测方法采用固定的数学方程式建立预测模型，其运算量相对较小，可以保证计算速度，但没有自学习和自适应能力[6]。随着电力系统复杂度的演变，其时变性、非线性和不确定性特点日渐突出，这样就难以建立一个准确的数学模型来进行预测[7]。为解决该问题，周涛[8]提出了一种改进的神经网络算法，以预测城市中长期电力需求，进而为城市电力系统的建设提供参考，但预测精度还需改进。此外，动态神经网络在预测领域使用较多的是Elman神经网络[9]，但Elman神经网络经常陷入局部极值且收敛速度慢，迭代时间长。这些不足在一定程度上影响了模型的预测精度。

为此，结合上述的研究基础，本文提出并建立了基于核主成分分析–支持向量机(kernel principal component analysis-support vector machine，KPCA-SVM)的电力负荷最大值预测模型，并对此模型进行了详细设计与仿真验证。

1 电力负荷最大值的影响因素

要提高电力负荷最大值预测的准确性，就必须考虑到电力负荷最大值的影响因素。电力负荷最大值短期预测是以每天的电力负荷最大值为预测对象的，电力负荷最大值不同预测周期的影响因素是不一样的，主要有以下4方面[10]。

1）天气因素。在温度、湿度、雨雪、霜雾等诸多表征天气的要素中，温度是相对最为重要的一个，此外天气类型也存在一定影响。

2）社会因素。社会因素包括人口数量、经济发展水平以及不同时间段的电价变化。

3）特殊事件因素。由于特殊事件，配备具有特殊效用的大型用电设备对电力负荷最大值存在一定影响。自然灾害等特殊情况也会对电力负荷最大值产生影响。

4）其他因素。日期类型(工作日、节假日)、季节需求差异、人口规模变化、空气质量状况、实时电价等因素，在某种程度上都对电力负荷最大值具有影响。

本文只分析每天的电力负荷最大值的短期预测，因此其影响因素主要有温度、前1~2天的电力负荷最大值、当天的天气类型和日期类型等。

2 KPCA与SVM算法描述

2.1 KPCA算法

KPCA属于机器学习的范畴，是对主成分分析(principal component analysis，PCA)的非线性扩展[11]，它是一种基于核的保留全局特征的非线性数据降维方法，能够挖掘到数据集中蕴含的非线性信息[12]。

分解式(1)，可得到对应的特征方程：

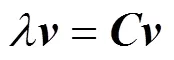
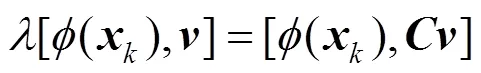
联合式(1)—(3)可得：

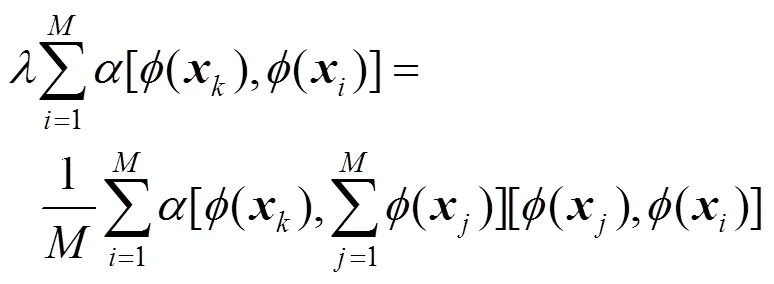
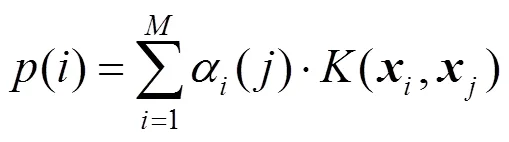
2.2 SVM回归算法

在机器学习领域中，SVM是一种有监督的学习模型，可用于识别分类、回归预测[14-15]。它可对有限样本信息在模型中的复杂性进行最佳优化，可解决小样本、非线性关系的问题。

约束条件为：

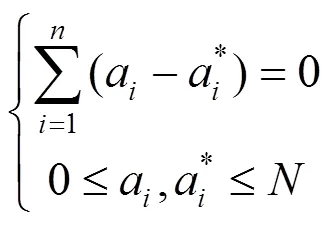
得到最终回归函数：

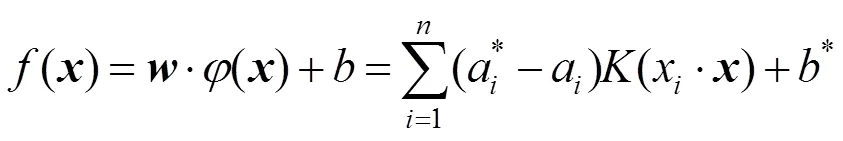
3 KPCA数据降维

3.1 样本数据的选取及预处理

单日的电力负荷最大值以安徽某市2018年7月12日至2018年9月30日，单日的负荷最大值作为基础数据，期间一共81天，所以可得到81组原始数据。

预测每天的电力负荷最大值属于电力负荷短期预测，影响因素方面选取了10个，分别为前一天的负荷最大值、当天8点的温度、当天的最高温度、当天的最低温度、前一天的平均温度、前一天的最高温度、前一天的最低温度、前2天的负荷最大值、当天的天气类型、当天的日期类型。未考虑季节需求差异、人口规模变化、空气质量状况、实时电价、特殊事件等因素。

电力负荷最大值的数据取自当地的电力公司，气温数据来自当地的气象局。以电力负荷最大值的10个影响因素为自变量，以当天的电力负荷最大值为因变量。并对自变量及因变量分别进行归一化预处理，采用如下归一化映射：

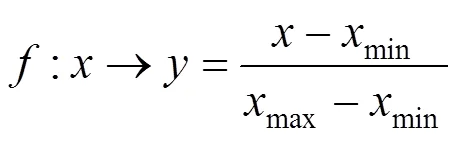
3.2 KPCA自变量降维处理

KPCA进行自变量的降维，在Matlab上编程实现，下面对其关键步骤部分进行说明。

1）数据预处理。进行标准化处理，处理后均值为0，方差为1。

2）采用高斯径向基核函数，求核矩阵。高斯径向基核函数：

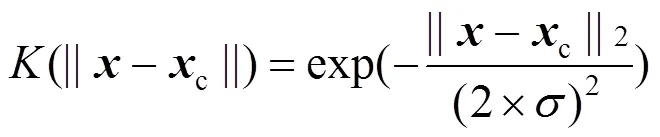
3）中心化矩阵，得到一个81´81的矩阵。

4）特征值分解。求协方差矩阵的特征向量和特征值，将主对角线上为特征值的对角阵变换成特征值列向量并对特征值按降序排列。

5）确定主元贡献率。计算各特征值的贡献率以及累计贡献率，并记录主元所在特征值向量中的序号，同时保存主元序号以及主元个数。

6）计算主元向量以及主元所对应的特征向量(负荷向量)，并构建主元对角阵。

经过KPCA降维处理之后，电力负荷最大值的影响因素由10维降至5维，其累计贡献率可达到93.70%。KPCA前5个主成分的单个贡献率及累计贡献率如表1所示。

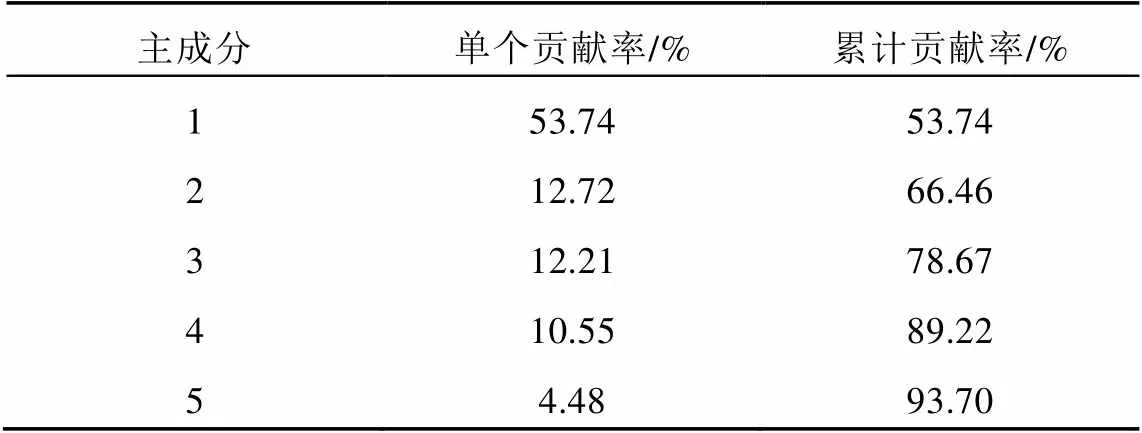
表1 KPCA对10种影响因素的处理结果

4 SVM预测模型

4.1 最佳参数的选择

以KPCA自变量降维处理后的5个主成分为输入，以当天电力负荷最大值为输出，采用径向基核函数，进行SVM预测模型的训练与测试，并从以上81组数据中，随机抽取54组作为训练集，27组作为测试集。算法流程如图1所示。

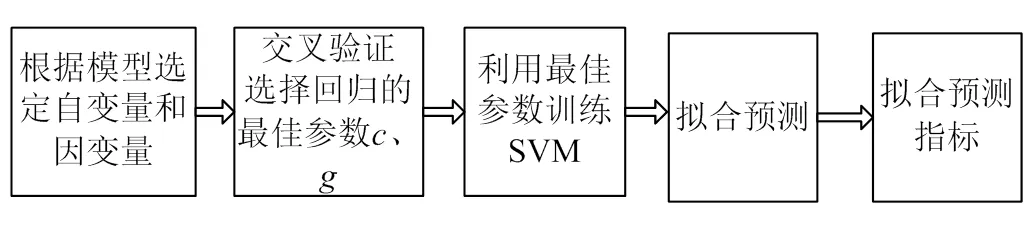
图1 SVM预测模型整体流程

SVM回归预测分析最重要的参数有2个，分别是惩罚参数与径向基核函数参数中的。表示对误差的宽容度，用于对分类间隔及错分样本进行平衡。越高，对出现的误差越不能容忍，容易产生过拟合；越小，则容易产生欠拟合[17]。过大或过小，都会使模型泛化性能变差，因此需要找到一个最佳的。

径向基核函数是一个以向量为自变量的函数，可以基于向量距离运算输出一个标量。是径向基核函数自带的一个参数，隐含地决定了数据映射到新的特征空间后的分布。其值越大，支持向量越少，其值越小，支持向量越多[18]。支持向量的个数对训练与预测的速度存在影响。

关于SVM回归预测分析最佳、的优化选取，目前还没有公认统一的最好方法，比较常用的方法就是让和在一定的范围内取值，对于取定的和，把训练集作为原始数据集并利用K折交叉验证(K-fold cross validation，K-CV)方法在此组和下验证预测准确率，最终取预测准确率最高的那组和作为最佳的参数。

首先进行粗略的寻找，观察粗略寻找的结果后再进行精细选择。图2—5分别是、粗略寻找结果等高线图，粗略寻找结果3D视图、精细选择结果等高线图、精细选择结果3D视图。粗略寻找的为1.74，为1；精细选择的为1，为2.83。

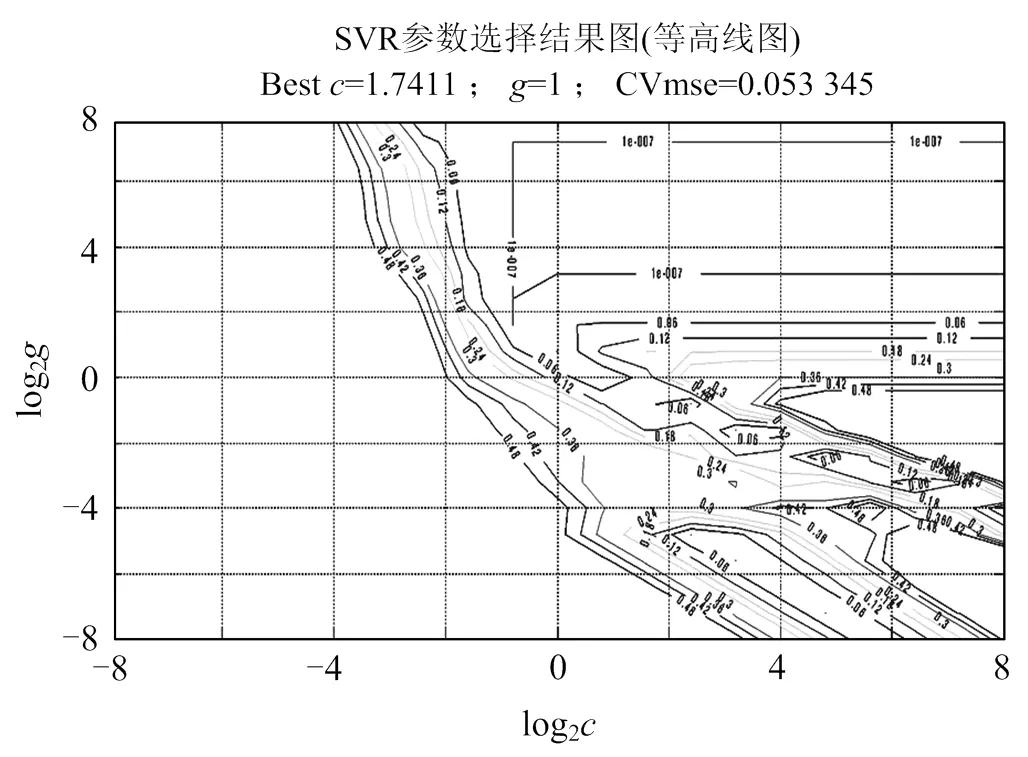
图2 粗略寻找结果等高线图

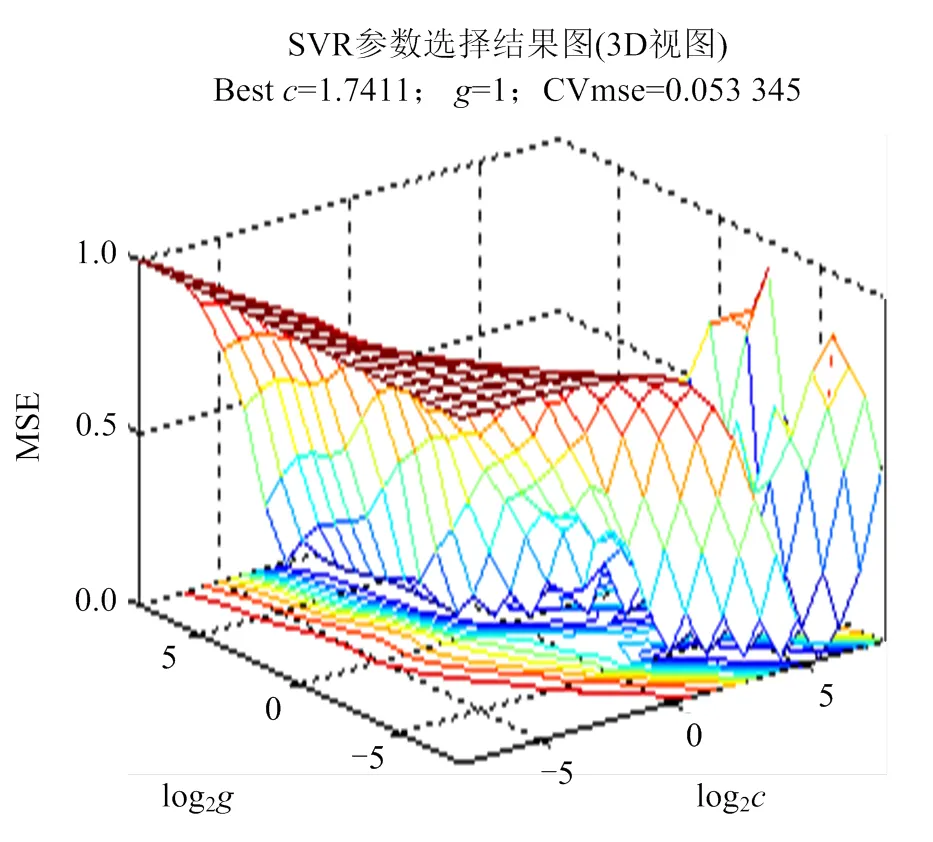
图3 粗略寻找结果3D视图

4.2 SVM训练与回归预测

从81天的电力负荷最大值数据集中，随机选取54天的数据，利用上面得到的最佳参数和对SVM模型进行训练，然后再对随机选取的27天的数据进行回归预测。最终预测出27天的电力

负荷最大值，并与其实际负荷最大值进行比较，仿真结果如图6所示。

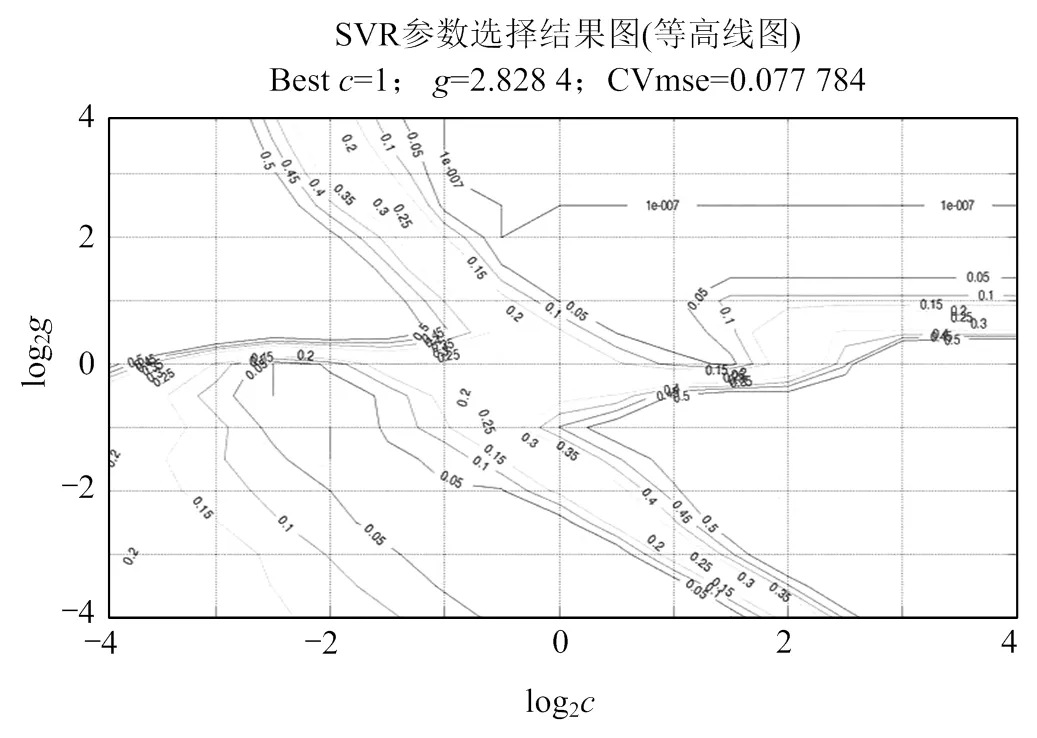
图4 精细选择结果等高线图

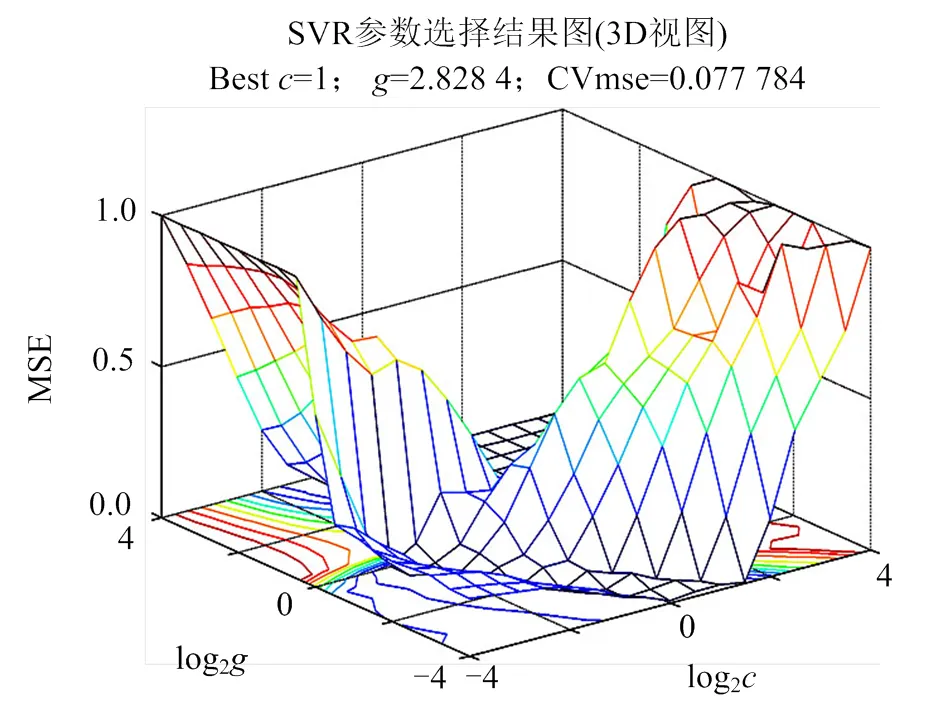
图5 精细选择结果3D视图

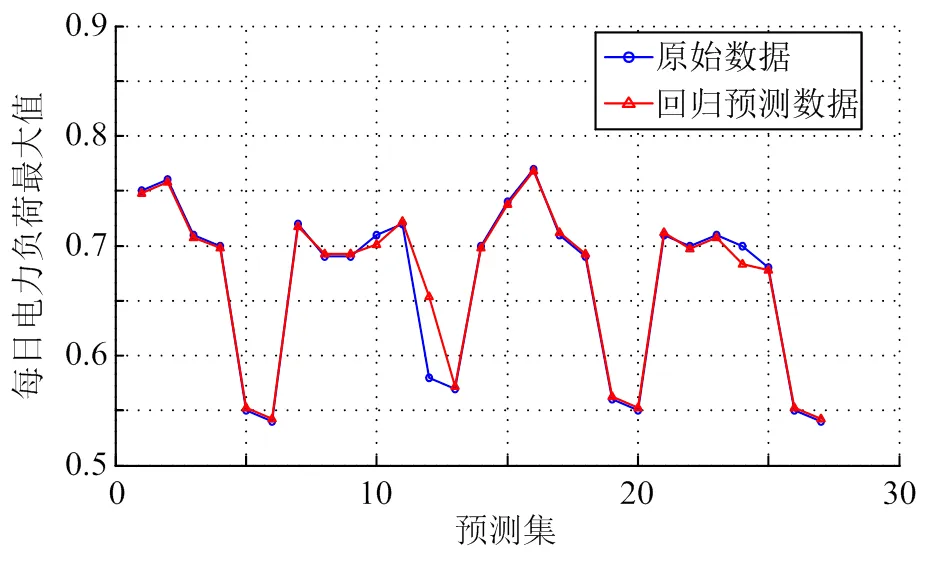
图6 SVM回归预测结果图

4.3 预测结果分析

预测误差为预测值与实际值之差，相对预测误差为预测误差与实际值的比值。预测误差图与相对预测误差图分别如图7、8所示。由图可知预测的第10、12、24天的误差相对较大，其中第12天的误差最大，其他的预测结果基本准确，总体上具有较高的预测精度。最后，求得预测结果的均方误差MSE=0.0041，相关系数=0.9631。

图7 SVM预测的误差图

图8 SVM预测的相对误差图

5 结论

1）选出对当天电力负荷最大值有重要影响的10个因素，采用KPCA算法进行降维。降维后得到的5维数据的累计贡献率可以达到93.70%，这表明KPCA算法在电力负荷数据降维处理上的有效性。

2）采用交叉验证选择SVM回归的最佳参数，先后进行粗略寻找和精细选择，拟合预测结果较为理想，表明交叉验证在选择SVM回归预测最佳参数上的必要性。

3）预测结果的均方误差达到了0.004 1，相关系数达到了0.963 1，表明基于KPCA-SVM的电力负荷最大值预测模型具有很好的预测效果。

4）融合KPCA降维算法和SVM预测模型对电力负荷最大值的较为理想的预测，表明机器算法应用于电力行业的潜在价值和良好前景。

[1] 梁青艳，孙彦广．钢铁企业电力负荷动态预测建模问题的应用研究[J]．科学技术与工程，2018，18(16)：44-54．

[2] 蔡秋娜，张乔榆，刘思捷，等．市场环境下考虑多因素影响的母线负荷预测方法[J]．广东电力，2019，32(8)：65-72．

[3] 陈潇雅，刘志坚，刘晓欣，等．基于长期负荷预测和联络分析的配电网规划[J]．广东电力，2019，32(3)：59-65．

[4] 杨博宇，陈仕军．电力负荷预测研究综述及预测分析[J]．四川电力技术，2018，41(3)：56-60．

[5] 郭威，巴秀玲．基于神经网络的电力系统负荷预测问题研究[J]．自动化与仪器仪表，2017(10)：192-194．

[6] 肖白，周潮，穆钢．空间电力负荷预测方法综述与展望[J]．中国电机工程学报，2013，33(25)：78-79．

[7] 邹京希，曹敏．基于总体测辨和人工神经网络的负荷建模及预测方法[J]．电力系统及其自动化学报，2018，30(8)：108-112．

[8] 周涛．基于改进神经网络的电力系统中长期负荷预测研究[J]．电气应用， 2013，32(4)：26-29．

[9] 杨楠，叶迪，周峥．基于NACEMD-Elman神经网络的风功率组合预测[J]．水电能源科学，2018，36(9)：209-211．

[10] 胡朝举，李云霞．关于电力负荷影响因素及智能预测方法的研究[J]．通信电源技术，2018，35(2)：231-232．

[11] 许杏花，潘庭龙．基于KPCA-RF的风电场功率预测方法研究[J]．可再生能源，2018，36(9)：1323-1327．

[12] 刘剑，刘丽华．基于KPCA与SVM的混合核交通流数据检测[J]．沈阳建筑大学学报(自然科学版)， 2018，34(5)：921-928．

[13] 李军，王秋莉．KPCA-KELM在短期交通流量预测中的应用[J]．江苏大学学报(自然科学版)，2018，39(5)：570-575．

[14] 胡伟，张玮灵，闵勇．基于支持向量机的电力系统紧急控制实时决策方法[J]．中国电机工程学报，2017，37(16)：4567-4576．

[15] 简献忠，顾祎婷．一种基于全过程优化支持向量机的短期电力负荷预测方法[J]．电力科学与工程，2018，34(11)：45-51．

[16] 鞠建波，胡胜林，祝超．一种改进的支持向量机回归故障预测方法[J]．电光与控制，2018，25(1)：6-9．

[17] 吐松江·卡日，高文胜，张紫薇．基于支持向量机和遗传算法的变压器故障诊断[J]．清华大学学报(自然科学版)，2018，58(7)：623-629．

[18] 许洪华，李勇，施恂山．基于振动噪声SC与SVM的变压器局部过热故障诊断[J]．陕西电力，2017，45(6)：11-17．

Short-term Prediction Method of Maximum Power Load Based on KPCA-SVM Model

ZHANG Yongwei1, PAN Qiaobo2

(1. Telecommunication Engineering Department, Anhui Post and Telecommunication College, Hefei 230000, Anhui Province, China; 2. Huadian Electric Power Research Institute Co., Ltd., Hangzhou 310030, Zhejiang Province, China)

The maximum power load is an important part of power enterprise dispatching work. The accuracy of its prediction results will have an important impact on the distribution of power, the effective utilization rate of power, the quality of power supply service and the development of power system. Based on the 81-day maximum power load data of a city in Anhui province, 10 factors influencing the maximum power load of that day were selected, and the influencing factors reduced from 10 dimensions to 5 dimensions by kernel principal component analysis(KPCA). The cumulative contribution rate can reach 93.70%. The best parameters of SVM regression were selected by cross validation. 54 groups of data were randomly selected to train SVM prediction model. Finally, 27 groups of data were fitted and predicted. The mean square error of fitting prediction was 0.0041, and the correlation coefficient was 0.9631. The results show that the KPCA combining the SVM prediction model for maximum power load has good prediction ability.

power system; load; kernel principal component analysis (KPCA); support vector machine(SVM); prediction model

10.12096/j.2096-4528.pgt.19010

2019-01-16。

国家科技支撑计划项目(2015BAA06B02)。

Project Supported by National Science and Technology Support Program of China (2015BAA06B02).

(责任编辑 辛培裕)