基于深度学习的小电流接地系统故障选线方法

张国栋，蒲海涛，刘凯

基于深度学习的小电流接地系统故障选线方法

张国栋1，蒲海涛1，刘凯2

（1．山东科技大学电气信息系，山东省 济南市 253500；2．洛阳供电公司，河南省 洛阳市 471000）

小电流接地系统的单相接地故障选线问题目前仍没有完全解决。为了提高单相接地故障选线成功率，提出一种基于深度学习网络的选线方法。首先，利用PSCAD搭建了中性点不接地系统仿真模型，通过设置每条线路在不同接地电阻下的故障，得到基于各出线零序电流幅值和相角的样本数据，并将样本数据分为训练集、验证集和测试集3部分。其次，基于Keras搭建了深度学习神经网络，利用训练集和验证集数据对该网络进行训练。最后，利用测试集数据对训练好的模型进行测试。结果表明，该方法具有建模简单、成功率高及选线不受过渡电阻影响的特点。

小电流接地系统；单相接地故障；故障选线；深度学习

0 引言

我国10~35 kV配电网多为中性点不接地或中性点经消弧线圈接地的小电流接地系统[1-4]。小电流接地系统发生单相接地故障时，接地电流小，保护器无需跳闸，可以继续运行1~2h，具有供电可靠性高的优点。由于故障电流小，在消弧线圈、故障点过渡电阻等因素的影响下，其故障选线问题仍未得到完全解决。

国内外学者对故障选线进行了大量研究。龙茹悦等[5]分析了特征频段内的馈线零序阻抗性质，提出了针对谐振接地系统的故障选线新方法；方毅等[6]分析了谐振接地系统经高电阻接地时的暂态能量特征，并提出了相应选线方法；朱永利等[7]将S变换与混沌振子系统相结合进行故障选线；蒋凯等[8]利用高维随机矩阵进行故障选线；文献[9-11]将遗传算法等优化算法与传统BP神经网络相结合，提高了选线正确率；徐铭铭等[12]提出了基于模型识别的谐振接地系统故障选线方法；沈兴来等[13]将群体比幅比相法、五次谐波比相法、小波分析法综合在一起，利用模糊理论判断故障线路；刘谋海等[14]通过希尔伯特‒黄变换(Hilbert-Huang transform，HHT)提取故障后零序电流高频分量确定故障线路；陈奎等[15]建立了较为详细的电弧模型，利用支持向量机进行故障选线；邵祥等[16]提出了基于改进动态时间弯曲(dynamic time warping，DTW)距离的接地故障波形互相关度聚类选线方法；魏鑫等[17]利用Hausdorff距离算法分析故障暂态零序电流差异程度，并进行故障选线。

以上研究所采用的选线方法可分为两大类：1）采用各种数学变换提取故障电流的暂态分量或稳态分量，利用故障线路与非故障线路的差异性进行选线，其特点是数学运算较为复杂，且选线结果易受干扰因素影响；2）采用优化算法与传统浅层学习(人工神经网络、支持向量机)相结合的方法，其特点是建模较为复杂，选线正确率也有待于进一步提高。

Keras是一个由Python编写的深度学习框架，便于构建深度学习网络并进行训练和测试。本文构建了基于Keras的深度学习网络，用于故障选线，具有计算简单、选线正确率高的优点。

1 深度学习算法

深度学习的概念自2006年由Hilton提出后，获得了巨大的发展[18-19]。深度学习采用了与传统神经网络类似的分层结构，如图1所示，系统包含了输入层、隐藏层和输出层。但是二者又有以下不同点：

1）隐藏层不同。传统神经网络仅包含一个隐藏层，深度学习网络可以包含多个隐藏层，而且每层可以包含更多的节点(神经元)。这使得深度学习网络可以描述更复杂的函数，从而为监督式学习提供了更强大的框架。

2）训练方法不同。传统神经网络采用BP算法进行训练，往往容易导致收敛于局部最小值；深度学习网络采用layer-wise的训练机制，在提高训练速度的同时，更有利于得到全局最优解。

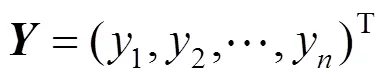
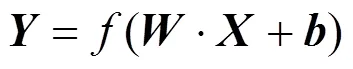
式中：列向量表示该层输入数据；为系数矩阵，假设该层节点数为m，其上一层节点数为n，则为阶矩阵；为m阶偏置列向量。

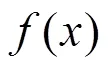
2 选线系统仿真建模

2.1 选线整体流程

图2为基于深度学习的小电流接地系统故障选线流程图。首先在PSCAD下搭建某10kV配电网。仿真过程中，令每条线路依次发生单相接地故障，提取包括故障线路在内的所有线路的零序电流分量，利用FFT变换，得到每条线路零序电流的幅值和相角作为样本数据，将故障线路编号作为标签数据，对深度学习神经网络进行训练，训练完成后即可利用新数据进行选线。

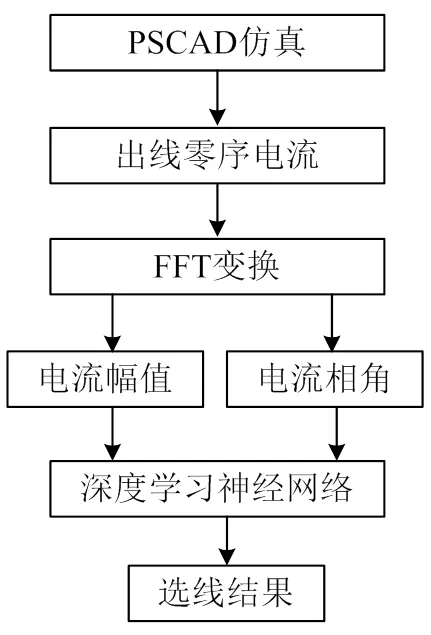
图2 故障选线流程

2.2 一次系统建模

参照某实际配电网，在PSCAD/EMTDC中搭建仿真系统，如图3所示。该配电网具有10条出线，变电站位于城区，线路采用电缆、架空线混合方式，相关参数见表1、2。

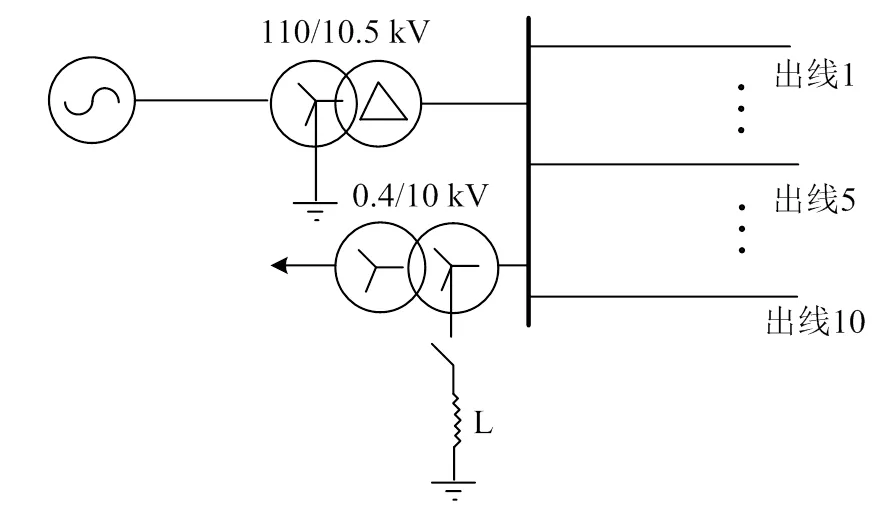
图3 仿真系统接线示意图

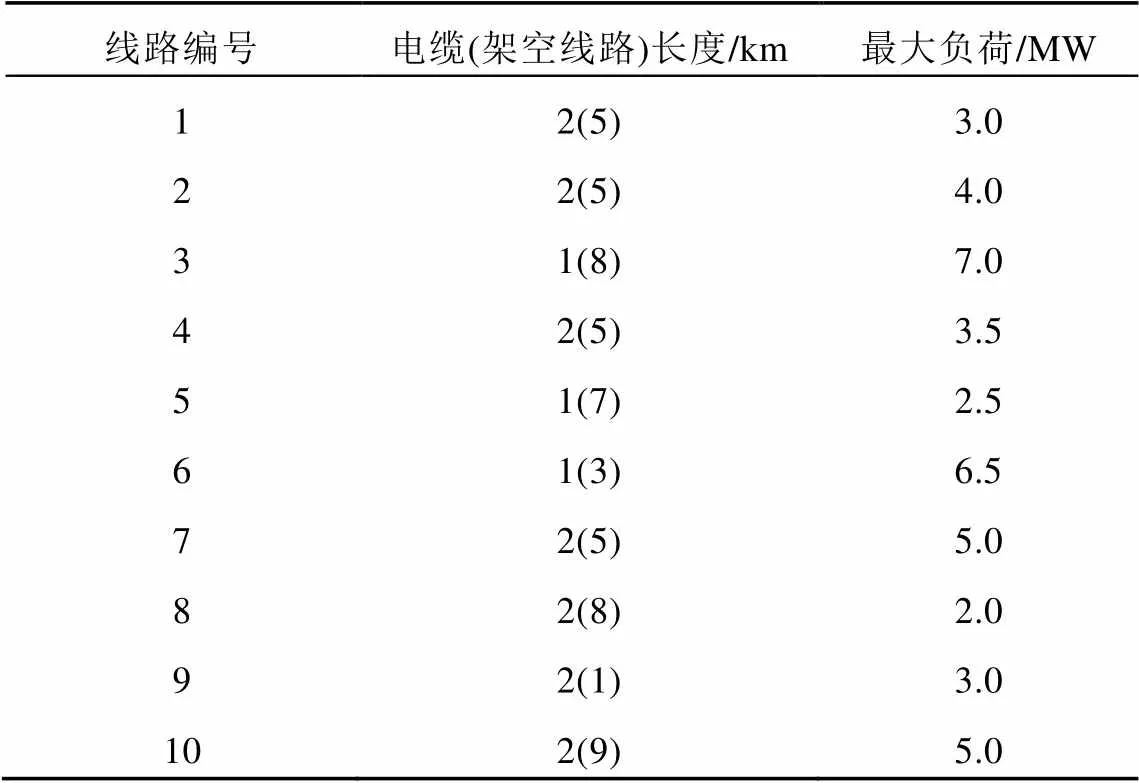
表1 出线参数

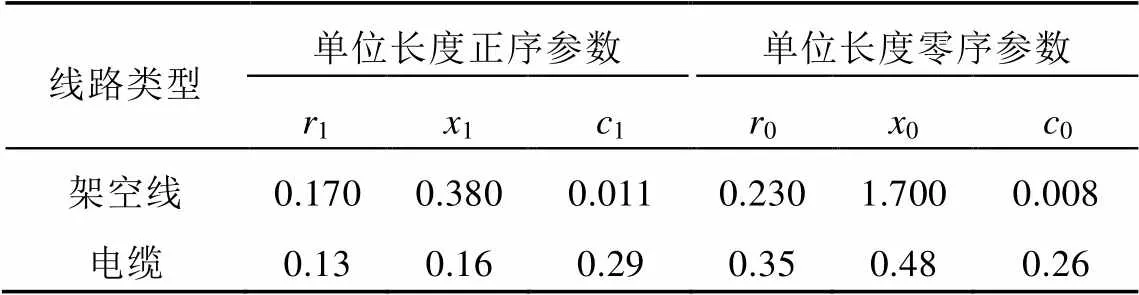
表2 出线阻抗参数

2.3 深度学习网络架构

深度学习网络包含可训练参数和超参数2部分。可训练参数是指网络在训练过程中确定的参数，主要为各层间的连接矩阵以及偏移量。超参数是指需要人为确定的参数，主要包括隐藏层的层数、每层单元数和每层激活函数等。对于超参数的确定，目前尚未有指导性公式可以参考，往往凭经验通过反复试验来确定。

通过试验，本文确定了深度学习神经网络架构，如表3所示。

表3 深度学习神经网络架构

注：总参数为39562个，可训练参数为39562个。

1）输入层。输入层接收样本输入数据，其节点数取决于样本数据的数量。本文中采用每条线路零序电流的幅值和相角作为样本数据，共计10条线路，因此样本数据的数量为20，即输入层节点数为20。

2）隐藏层1。隐藏层1将输入层输入的样本数据映射到每一个节点上，其节点数为256，连接矩阵12的阶数为256×20=5120，偏置量的阶数为256×1，即总参数为5376。

3）丢弃层(Dropout)。丢弃技术是防止网络过拟合、增强泛化能力的重要手段之一。该层不需要训练，而是将上一层(隐藏层1)输出的数据按一定比例丢弃(置零)。

4）隐藏层2。该层确定的节点数为128，连接矩阵阶数为128×256，偏置量的阶数为128×1，总参数为32896。

5）输出层。深度学习神经网络用于解决10条线路中故障线路的选择问题，其本质上属于多分类问题。输出层节点输出每条线路故障的概率，概率最大者即判定为故障线路。仿真系统中有10条线路，因此输出层节点数取10。与上一层连接矩阵阶数为10×128，偏置量的阶数为10×1，总参数为1290。

6）各层激活函数。采用激活函数可以使神经网络表示复杂的非线性函数。深度学习神经网络中，各隐藏层采用Relu函数作为激活函数，输出层输出的是每条线路的故障概率，因此采用Softmax函数作为激活函数。

3 算例分析

3.1 中性点不接地方式

系统采用中性点不接地运行方式，每条线路分别采用单相直接接地、经500Ω电阻接地、经1000Ω电阻接地3种故障类型，经FFT采样后，得到1850组样本。把所有样本随机分成训练集、验证集、测试集3组。其中测试集为150组样本，训练集与验证集比例为9꞉1。

为了加速深度学习神经网络训练过程中的收敛，需要对样本数据进行预处理。数据预处理主要包括以下2个方面：

1）特征数据归一化。可以利用式(2)将所有的特征数据都处理到(0,1)区间范围内。

2）标签数据二值化。原始标签数据为故障线路编号，为了与网络输出的概率值相对应，需要将其转化为十位二进制数据。每一位二进制数据对应一条线路，其中非故障线路对应数据为0，故障线路对应数据为1。如第3条线路发生故障，其原始标签为3，二值化处理后的数据为0010000000。

将经过预处理的样本数据输入到搭建好的深度学习神经网络中进行训练，训练迭代次数为50次。损失函数值曲线如图4所示，可以看出，随着迭代次数的增加，损失函数值越来越小，表明网络输出值与目标值(标签值)越来越接近。

图5为精确度曲线，可以看出，随着训练次数的增加，网络在训练数据集和验证数据集上表现出来的预测精确度越来越高。

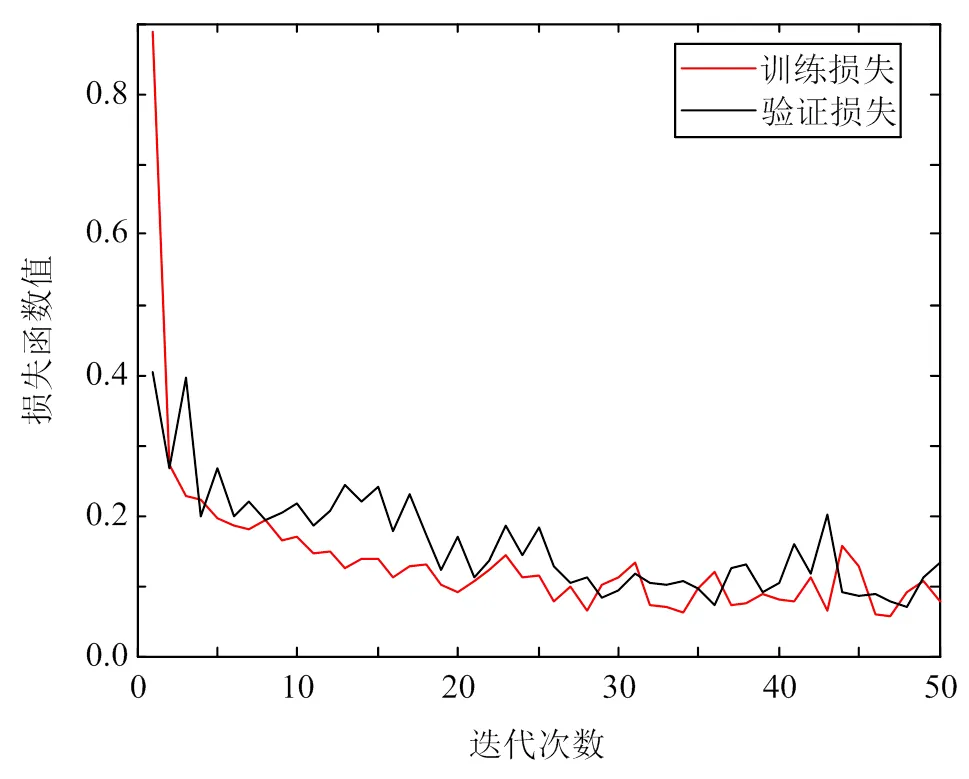
图4 损失函数值曲线‒1

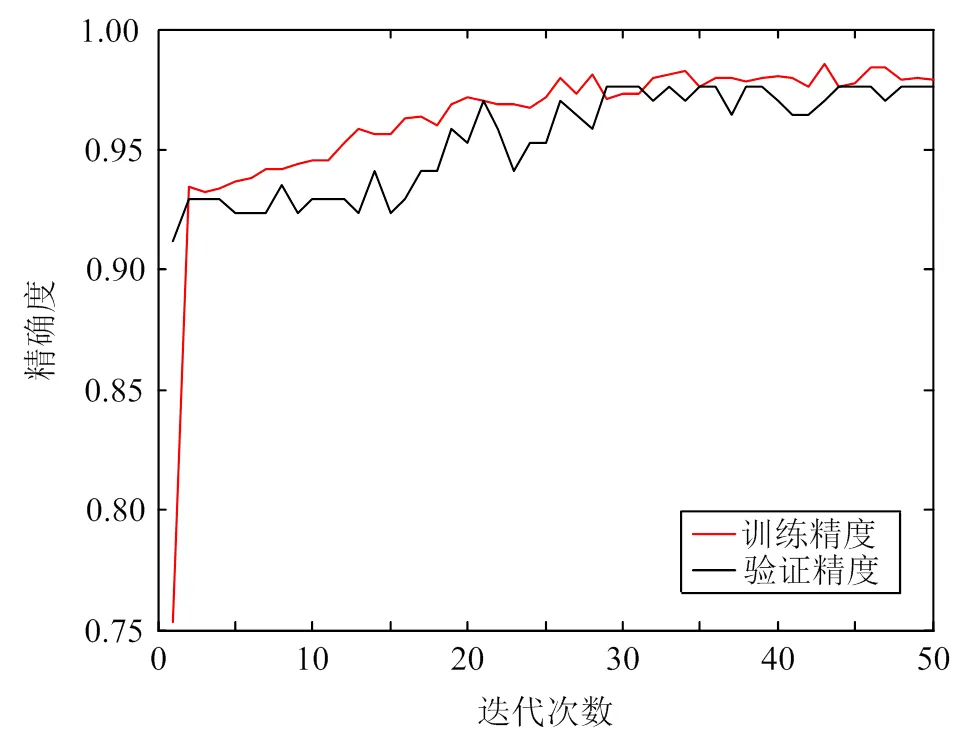
图5 精确度曲线‒1

训练结束后，利用预留的150组测试集数据对训练好的神经网络进行测试。测试结果如表4所示。表4中主对角元素的数值表示相应线路故障时判断正确的次数；非主对角线元素的数值表示判断错误的次数。以第1行、第1列数据为例，该数据值为11，表示线路1发生故障时，判断正确的次数为11；线路1所在列的非主对角线元素值均为0，表示未发生误判。作为对比，再以线路8所对应的第8列数据为例进一步说明。该线路对应的主对角线元素值为14，即判断正确的次数为14。非主对角线元素有2个非零值，其中：第1个非零值位于第8列第2行，数值为1，其含义为实际发生故障的线路为线路8，判断结果为线路2，判断错误次数为1次。同理，第2个非零值位于第8列第3行，数值为1，表示实际故障发生在线路8，判断结果为线路3，判断错误次数为1次。综上分析，测试集样本数量为150，判断正确次数(主对角线元素之和)为148次，判断错误次数(非主对角线元素之和)为2次，正确率达到98.7%。

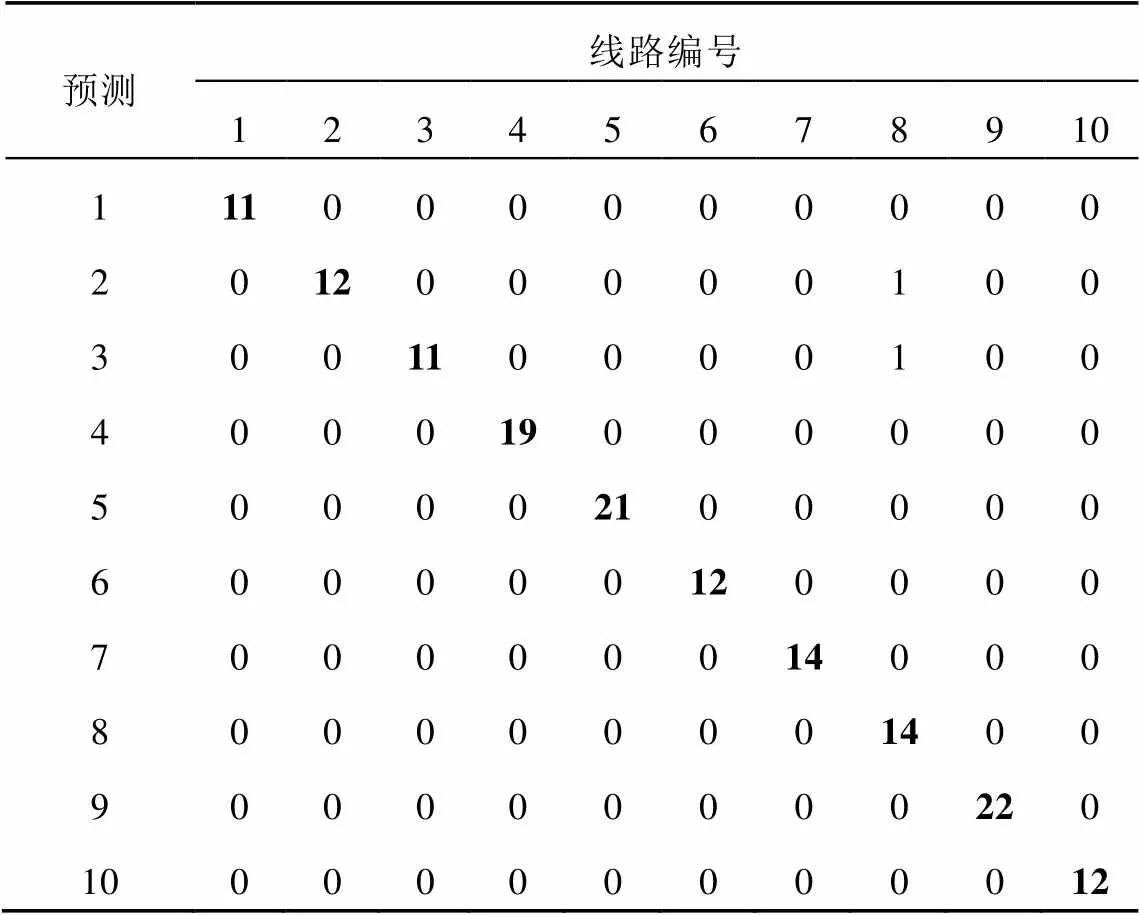
表4 测试结果混淆矩阵‒1

3.2 中性点经消弧线圈接地方式

系统采用中性点经消弧线圈接地运行方式，过补偿度为10%。每条线路分别采用单相直接接地、经500Ω电阻接地、经1000Ω电阻接地3种故障类型，经FFT采样后，得到1930组样本。把所有样本随机分成训练集、验证集、测试集3组。其中测试集为150组样本，训练集与验证集比例为9꞉1。

训练过程中的损失函数值曲线和预测精确度曲线分别如图6、7所示。

训练结束后，利用测试集数据进行测试，测试结果如表5所示。可以看出，线路7发生故障时，误判次数较多，其中误判为线路3故障的次数为1次，误判为线路5故障的次数为2次，误判为线路6故障的次数为1次，总计误判次数为4次。测试集样本数量为150，判断正确次数(主对角线元素之和)为145次，判断错误次数(非主对角线元素之和)为5次，正确率达到96.7%。

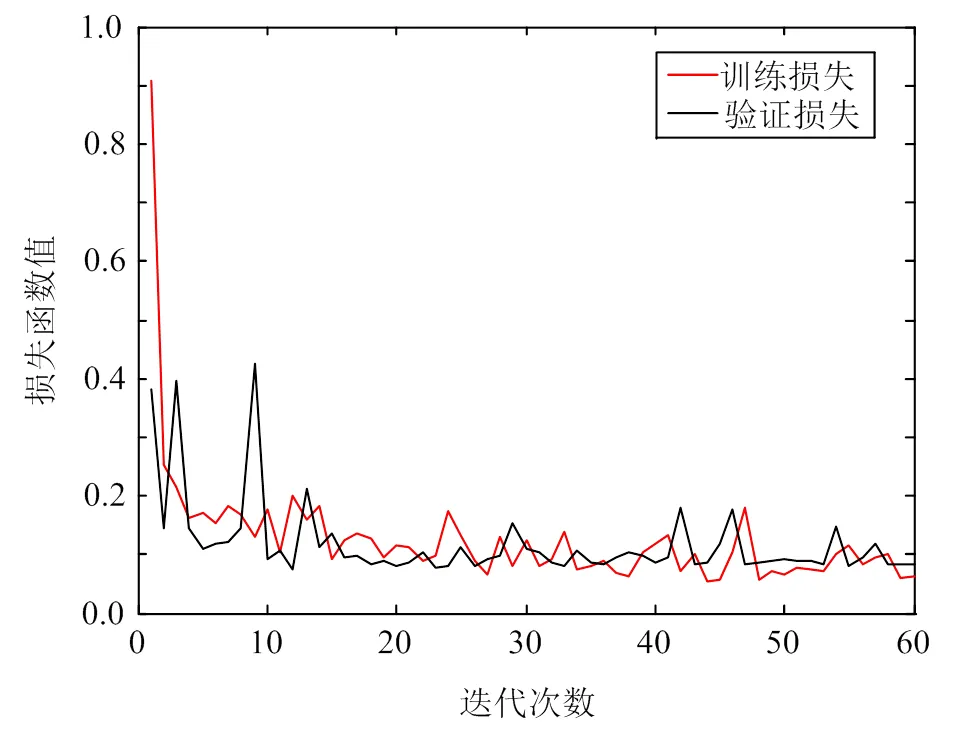
图6 损失函数值曲线‒2

图7 精确度曲线‒2

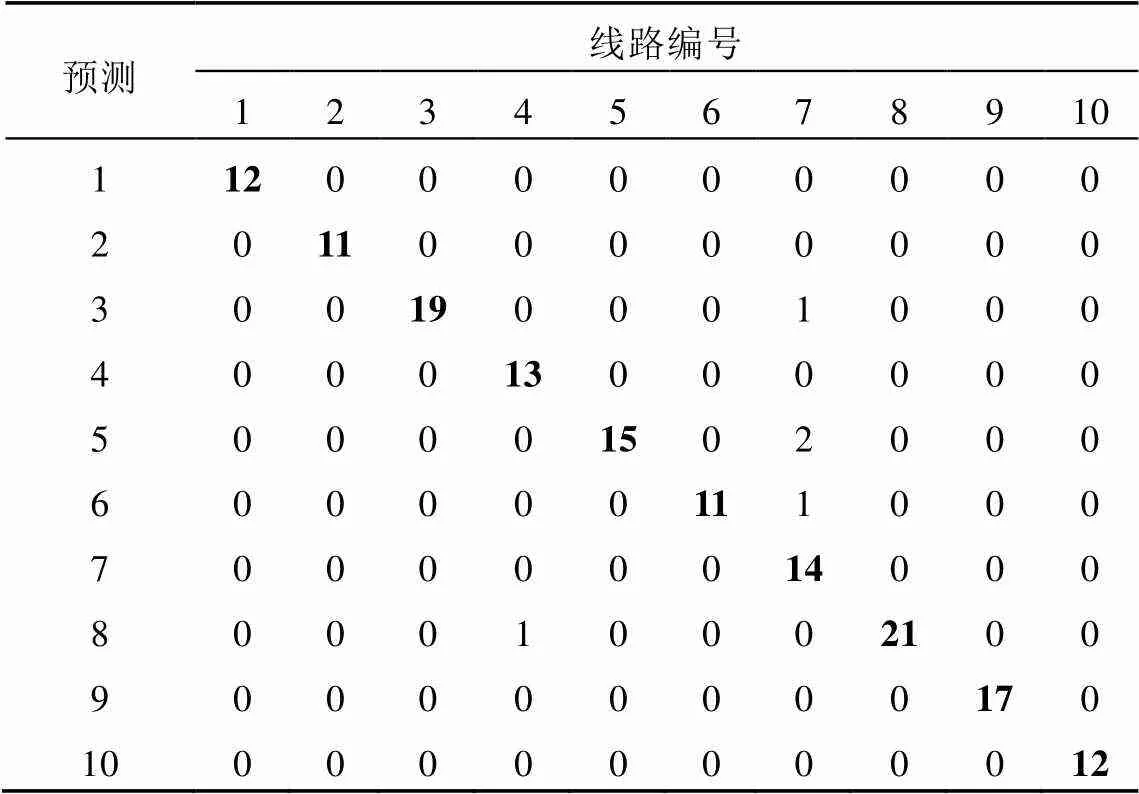
表5 测试结果混淆矩阵‒2

3.3 考虑故障点电弧的仿真模型

前述仿真过程中，未考虑接地点产生电弧的情况。为尽可能真实地反映实际系统情况，参照文献[20]中的方法，建立了Mayr电弧模型。经FFT采样后，得到1930组样本。把所有样本随机分成训练集、验证集、测试集3组。其中测试集为150组样本，训练集与验证集比例为9꞉1。

训练过程中的损失函数值曲线和预测精确度曲线分别如图8、9所示。

训练结束后，利用测试集数据进行测试，测试结果如表6所示。可以计算出，在电弧影响下，判断正确率下降至94.7%。

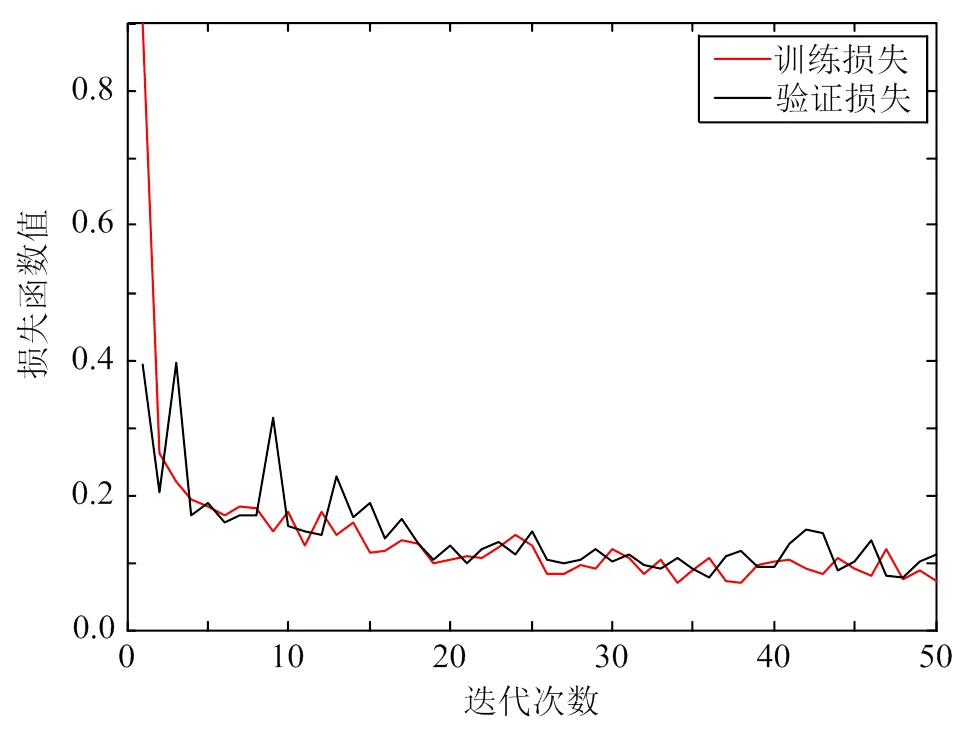
图8 损失函数值曲线‒3

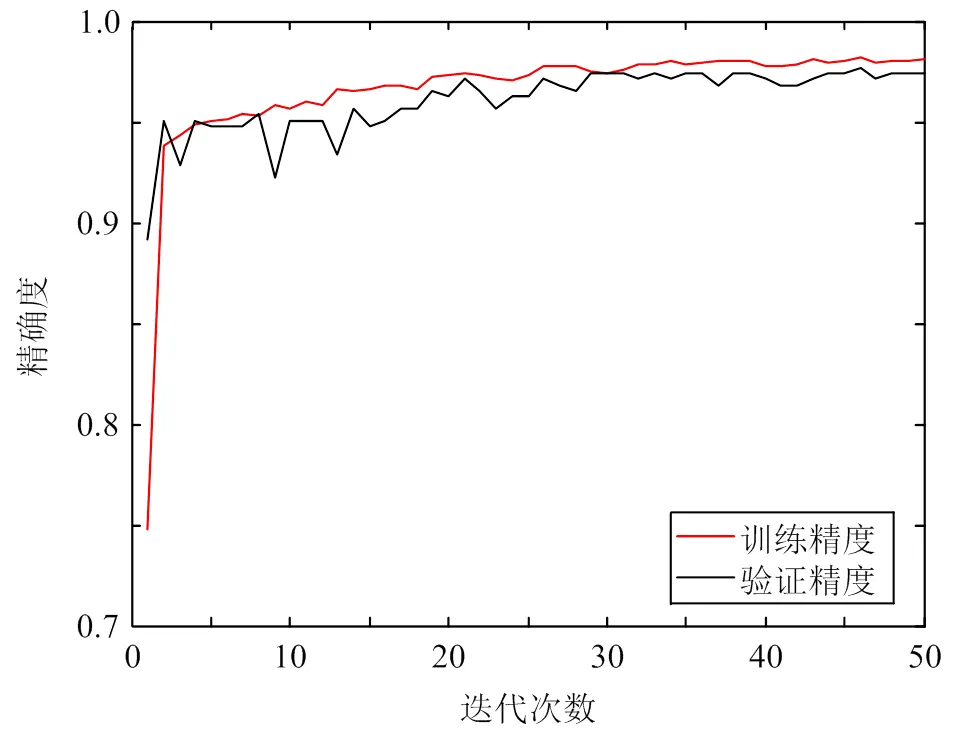
图9 精确度曲线‒3

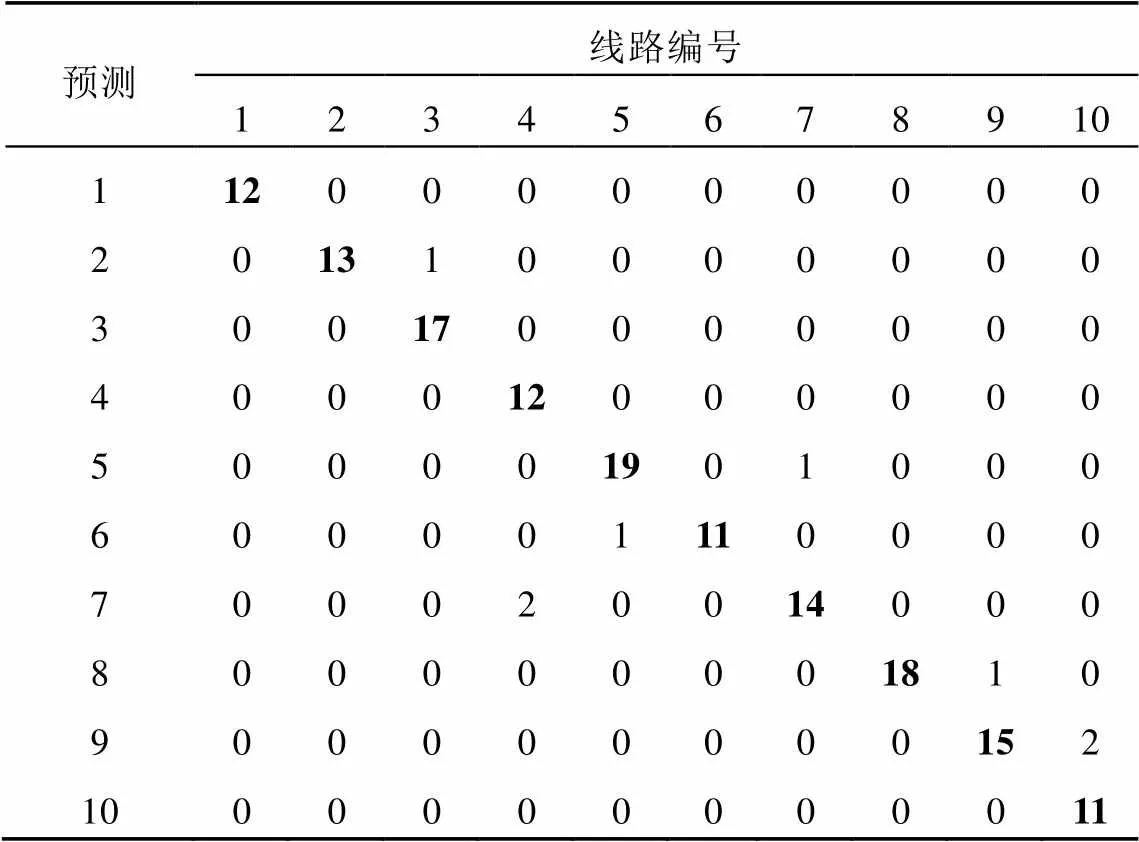
表6 测试结果混淆矩阵‒3

4 结论

构建了基于深度学习框架的小电流接地系统单相接地故障的选线模型。在PSCAD下搭建仿真模型，通过仿真获得训练数据。利用仿真所得数据对深度学习神经网络进行训练，将训练好的模型用于单相接地故障线路的选择。结果表明，对于中性点不接地系统的单相接地故障，选线正确率达到了98.7%；对于中性点经消弧线圈接地系统的单相接地故障，选线正确率达到了96.7%，且选线结果不受过渡电阻影响；引入电弧模型后，选线正确率仍能保持94.7%，说明该方法有效。

[1] 陈皓，田新和，高传薪，等．直流微电网故障定位研究综述[J]．广东电力，2019，32(7)：44-51．

[2] 徐栋杰，刘文泽，李晓华．开关型消弧装置的故障选相及选线方法[J]．广东电力，2019，32(1)：125-131．

[3] 汪洋．基于小波分解-暂态信号的综合极性比较故障选线法[J]．电网与清洁能源，2017，33(6)：59-66．

[4] 刘宏伟，朱东坡，刘捷，等．配电网中性点经小电阻接地方式下的小电阻选取[J]．电网与清洁能源，2018，34(7)：31-37．

[5] 龙茹悦，黄纯，汤涛，等．一种谐振接地系统的配电线路接地故障选线新方法[J/OL]．电力系统保护与控制：1-9[2019-11-21]．https://doi.org/10.19783/j.cnki.pspc.181495.

[6] 方毅，薛永瑞，宋华茂，等．谐振接地系统高阻接地故障暂态能量分析与选线[J]．中国电机工程学报，2018，39(19)：5636-5645．

[7] 朱永利，尹金良．人工智能在电力系统中的应用研究与实践综述[J]．发电技术，2018，39(2)：106-111．

[8] 蒋凯，童晓阳，梁晨．基于随机矩阵的配电网故障选线方法研究[J]．电工技术，2018(13)：1-4．

[9] 罗浩杰，张栋柱，李民强，等．基于人工神经网络小电流接地选线方法研究[J]．四川电力技术，2016，39(6)：36-40．

[10] 薛太林，侯隽朗，张建新．基于GA优化BP神经网络小电流接地系统故障选线方法[J]．电气自动化，2018，40(2)：66-69．

[11] 但扬清，赵伟，朱艳伟，等．基于ABC-DNN的小电流接地故障选线方法[J]．智慧电力，2019，47(4)：46-52．

[12] 徐铭铭，高淑萍，常仲学，等．基于模型识别的消弧线圈接地系统单相接地选线方法[J]．电力系统保护与控制，2018，46(2)：73-78．

[13] 沈兴来，杨智．基于故障全信息的自适应模糊融合选线技术[J]．电力工程技术，2017，36(6)：90-95．

[14] 刘谋海，方涛，姜运，等．基于高频分量相关度分析的故障选线方法[J]．电力系统及其自动化学报，2017，29(2)：101-106．

[15] 陈奎，陈博博．基于改进暂态相关分析和支持向量机的电弧故障选线研究[J]．电力系统保护与控制，2016，44(24)：66-73．

[16] 邵祥，郭谋发，游林旭．基于改进DTW的接地故障波形互相关度聚类选线方法[J]．电力自动化设备，2018，38(11)：63-71．

[17] 魏鑫，舒乃秋．基于Hausdorff距离的配电网单相接地故障选线方法[J/OL]．电力系统及其自动化学报：1-12[2019-11-21]．https://doi.org/10.19635/j.cnki.csu-epsa.000244．

[18] 周怀春，胡志方，郭建军，等．面向智能发电的电站燃煤锅炉在线运行优化[J]．分布式能源，2019，4(3)：1-7．

[19] 潘玉松，陈旭伟，张鹏．传统火电厂建设智慧电厂的典型方向及构架体系[J]．分布式能源，2018，3(5)：48-53．

[20] 窦婷婷，姚元玺，陈鹏，等．基于ATP-EMTP的电弧建模及工程仿真[J]．山东大学学报(工学版)，2019，48(4)：102-108．

Fault Line Selection Method of Small Current Grounding System Based on Deep Learning

ZHANG Guodong1, PU Haitao1, LIU Kai2

(1. Department of Electrical and Information, Shandong University of Science and Technology, Jinan 253500,Shandong Province, China; 2. Luoyang Power Supply Company, Luoyang 471000, Henan Province, China)

At present, the single-phase grounding fault line selection problem of small current grounding system has not been completely solved. In order to improve the success rate of single-phase grounding fault line selection, a new method based on deep learning network was proposed. Firstly, the simulation model of neutral un-grounded system was built by PSCAD. By setting the fault of each line under different grounding resistors, the sample data based on the zero sequence current value and phase angle of each line was obtained out. The sample data was divided into three parts: training set, verification set, and test set. Secondly, a deep learning neural network was constructed based on Keras, and the network was trained using the training set and validation set. Finally, the trained model was tested using the test set. The results show that the method has the characteristics of simple modeling, high success rate and no influence of transition resistance.

small current grounding system; single- phase grounding fault; fault line selection; deep learning

10.12096/j.2096-4528.pgt.19103

2019-07-06。

教育部产学合作协同育人计划项目(201702064021)；山东科技大学济南校区教研项目(JNJG2017203)。

Project Supported by Ministry of Education's Cooperative Education Program Project (201702064021); Research Project of Jinan Campus of Shandong University of Science and Technology (JNJG2017203).

(责任编辑 尚彩娟)