直立式护岸渡槽船行波分布规律研究

翟正娟

（苏交科集团股份有限公司，南京210019）

1 前言

我国内河航运呈显著的船舶大型化、 通过频率密集化发展，这导致船行波问题日益严重［1-3］。 尤其在部分束窄河段 （如渡槽、 船闸引航道、 天然束窄段），船行波引起的水流紊乱问题尤为明显。 规模较大的船行波将产生船首偏角影响过往船舶正常行驶、恶化航道两岸码头待泊船舶泊稳，甚至产生掏刷水流，破坏两侧护岸的稳定性。

针对船行波的研究最早起于18世纪末，在Kelvin认为船在行驶过程中会产生横波和散波两种波形，两种频率的波相互叠加的峰值点为歧点，经分析及实践验证，歧点的连线为直线（成为歧线），且歧线与船舶行驶路径之间的角度成为开尔文角，且为相对固定值（19°～22°）［4］。 开尔文角示意如图1。

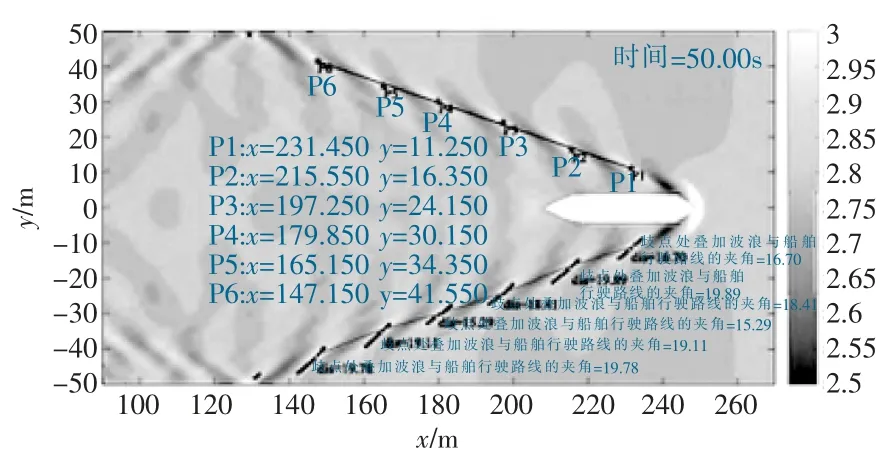
图1 开尔文角示意

Wilson通过对巴拿马12种船型大量行驶波浪数据统计，认为船行波在平面传播、分布上具有典型的二维性质，而最大波高随时间一直波动，在空间上又具有明显的三维性质［5-6］。 Raven将叠加波浪的最大波高定义为一个波浪序列中，相邻波峰和波谷之间的最大高程差，将波峰和波谷之间的时间历程定义为半个周期［7］。 船行波波高时间序列过程如图2。

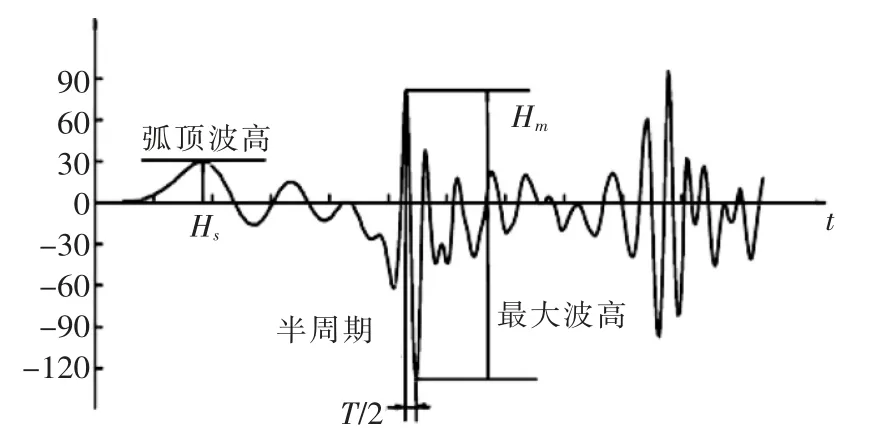
图2 船行波时间序列

王田艺认为，在直立式护岸区域，船行波受直立式岸墙反射影响，相互干扰、叠加，船行波规模远大于自然岸坡和斜坡式护岸［8-10］。

2 工程概况

工程隶属滨海枢纽工程，位于滨海县城南6km、入海水道与连申线交汇处。 滨海枢纽二期渡槽位于江苏省盐城市连申线（即通榆河）上，为给渡槽的入海水道泄洪通道创造条件，渡槽采用直立式挡墙结构，且航宽由现状的90m束窄为71m。二期地涵建于一期地涵北侧200m处，地涵长293.4m，口宽71m，航宽70.42m，与一期地涵连接段斜坡坡率为1∶12。 滨海枢纽二期地涵平面布置如图3，立面布置如图4。 工程段连申线最高通航水位2.24m，最低通航水位-0.37m，渡槽设计底高程3.67m。

图3 滨海枢纽二期渡槽平面布置

图4 滨海枢纽二期渡槽立面布置

3 三维模型建立

本文采用三维数值仿真模拟方法，探究直立式护岸下渡槽内船舶船行波分布规律。

3.1 船型选择及船舶模型建立

连申线航道规划等级为Ⅲ级航道，根据GB50139—2014《内河通航标准》及《京杭运河、淮河水系过闸运输船舶标准船型主尺度系列》，取1000t级货船为代表船型，设计尺度为58m×11.0m×3.1m（船长×宽×吃水）。 船舶模型如图5。

图5 设计代表船型概化

3.2 渡槽三维模型及计算工况

二期渡槽长293.4m，宽71m。 渡槽段三维模型及网格划分如图6。其中，模型采用立方体网格，网格间距设为2m，整个模型共有10402个网格和20605个网格节点。 本模型中船舶距离岸壁距离为1m。

选择最高通航水位作为计算工况，该工况下，河段水流自北向南，流量250m3/s，水位2.41m。

图6 二期渡槽三维模型网格划分

4 三维模型计算结果

4.1 船行波发展过程

设计代表船型进入渡槽后，船行波发展、传播过程如图7。

图7 1000t级货船渡槽中船行波发展过程

分析可知：

（1）在船舶前进过程中，船首部分挤压、推排船前水体，形成弧形壅水，并沿着开尔文角度方向相对船体向斜后方运动。

（2）船行波波峰出现在船首正前方区域，在向斜后方运动过程中按照间谐波的规律依次震荡，波峰、波谷交替出现的规律十分明显。 证明船行波具有显著的二维、三维性质。

（3）船行波在前4个周期中，与岸壁之间基本无相互干扰作用。 从第5个周期开始，船行波受岸壁的反射波作用影响，波峰线逐渐缩短，且波纹开始紊乱，与反射波的相互干扰作用逐渐明显。

（4）经对比，船首行波的规模、波高都显著大于船尾行波。 产生原因主要是船舶在船首推排水体形成波浪并逐渐传播，在传播过程中波浪能量逐渐消减，且波浪干涉、衍射作用也在一定程度上消减了波浪能量，减小了波浪规模。

4.2 不同吃水对船行波的影响

在船舶航速为5.0m/s 下，设置吃水分别为0.75，1.0，1.25，1.5m 4组对比工况。 船舶吃水模型设置如图8，各工况下在行驶45s时的船行波分布如图9。

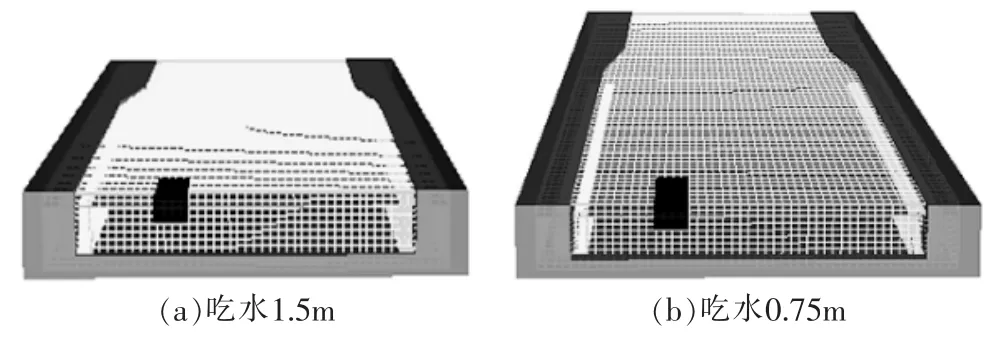
图8 不同吃水工况下模型

图9 不同吃水工况下船行波分布

分析可知：

（1）随着船舶吃水深度增加，船舶推开船前水体增大，船首壅水范围及船行波规模也单调递增。

（2）随着船舶吃水深度增加，波浪震荡幅度越大，相应地波谷高程也越低。

（3）在4组工况下，波浪周期及波浪长度基本一致。 可见不同吃水深度对船行波的波浪周期及波浪长度基本无影响。

（4）4组工况下，开尔文角的计算值在19.11°～21.94°之间，均在理论值范围内，可见从开尔文角的合理性方面，模型计算结果较为精确。

4.3 不同航速对船行波的影响

设置两组对比试验分析不同航速对船行波影响，即吃水深度在0.9m时，航速分别为5.20，5.70m/s时对船行波分布影响，以及吃水深度在1.40m时，航速分别为5.20，5.70m/s时对船行波分布影响。 计算结果如图10，图11。

图10 吃水深度0.9m船行波分布

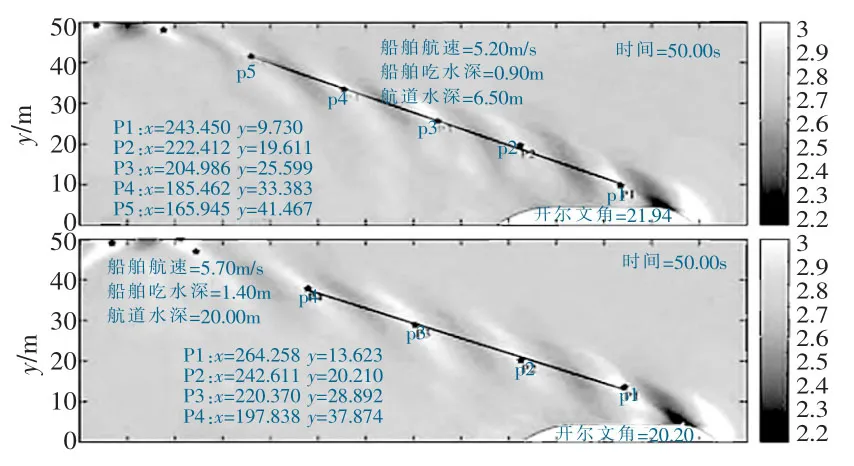
图11 吃水深度1.4m船行波分布

分析可知：

（1）在不同航速下，船行波分布形态略有区别。随着航速增大，在相同面积的范围内，歧点间距增大，数量减少。

（2）分析可知，船行波的波长与航速呈正比，随着航速增大，波长也随之增大。

（3）4组工况下，开尔文角的计算值在20.20°～21.94°之间，均在理论值范围内，可见从开尔文角的合理性方面，模型计算结果较为精确。

5 工程波高拟合计算

本文根据仿真试验计算的262 组数据，对J12229—2012《内河航道工程设计规范》附录C中的波高计算公式进行回归分析，迭代求解相关系数。计算如式（1）：

式中 Hc为船行波等效波高（m）；h为渡槽水深（m）；S0为船舶航迹线与直立式岸壁的距离 （m）；B为船舶宽度（m）；V为船舶航速（m/s）；g为重力加速度（m/s2）；d为船舶吃水深度（m）；α，β1，β2，β3均为待定求解系数。

对式（1）进行待定系数求解，得到滨海枢纽二期渡槽波高，如式（2）：

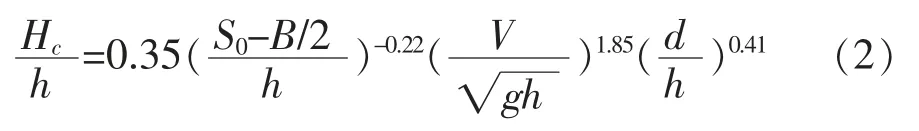
根据仿真试验计算262组数据，由式（2）与数值模拟计算值进行对比分析，其中部分计算点（图12中列出了86个计算点的精度分析情况）拟合公式波高计算结果精度如图12。

图12 拟合波高计算结果

分析可知，262组数据中，最大计算误差0.32m，最小计算误差0.00m，平均计算误差0.03m；计算误差比小于10%的数据共有227组，占全部样本的86.6%，计算误差比小于15%的数据共有240组，占全部样本的91.6%；三维数模计算值与拟合公式计算值的相关系数达0.963；可见采用回归分析拟合计算公式预测精度较高，能很好地反映实例工程的波高情况。

6 结语

（1）船行波波峰出现在船首正前方区域，在向斜后方运动过程中按照间谐波的规律依次震荡，波峰、波谷交替出现的规律十分明显。 可见船行波具有显著的二维、三维性质。

（2）船舶吃水深度增加，船舶推开船前水体增大，船首壅水范围、船行波规模也单调增大。 同时吃水深度对波浪周期及波浪长度基本无影响。

（3）船行波的波长与航速呈正比，歧点数量与航速呈反比。

（4）采用回归分析方法，验证了规范波高计算公式中的系数取值，得到了滨海枢纽二期渡槽船行波波高计算公式，且经验证，拟合公式计算精度较高，能很好地反映实例工程波高分布情况。

（5）针对船舶与岸壁距离、船型尺度、船型交汇情况、其他护岸型式对船行波的影响，有待进一步分析研究。