集对分析与可拓学耦合在节水灌溉后评价中的应用

卢家海，李爱云

（太原理工大学 水利科学与工程学院，太原 030024）

高效节水灌溉项目后评价指标体系应能反映项目工程本身的情况，以及在社会经济、环境等各个方面产生的效益和影响，并体现节水灌溉工程的特点，具有客观性、可操作性、通用性和可比性。 在确定评价对象和评价目的基础上，先进行后评价指标初选，分析各个评价指标在整个评价体系中的重要性，从而选择合适的评价指标来描述评价因素。 设置项目后评价指标时还要充分考虑其测定方法，度量标准和可操作性，从量的角度来分析项目的实际效果，同时为项目后评价的定性分析提供较为翔实的依据。而评价指标体系是衡量项目建设是否成功的一杆标尺，涵盖要素众多。高效节水灌溉项目的后评价是一项复杂的系统工程，其指标体系应能反映项目对社会、经济、环境、资源等诸多方面，其中大部分评价因素可通过调查研究进行定量分析，其他难以用确切的数值或数学方法进行表达或计算的指标，依靠评价专家积累的经验，对项目的成功度作出定性结论。

高效节水灌溉后评价涉及因素很多，且大多具有不确定性，同时传统模糊数学方法、人工神经网络等各类方法也有自身的局限性，如模糊数学难以区分相似指标的差异； 人工神经网络对初始权重过渡依赖，往往会使算法陷入极值；粗糙集理论方法在属性约简过程中可能删掉重要的评价因子，导致结果误差，可见评价问题至今尚未得到很好解决。 为此，人们引入可拓评价方法来分析节水灌溉项目，因该法能比较全面地考虑各个因素，但其计算关联度时常以区间中点为最优，而这会遗漏重要的约束条件，导致结果与实际某些情况存在差异，而集对分析方法可很好解决中间转化问题，但在评价中难以确定差异度系数，如将两者耦合起来，既可应用可拓理论在计算关联度方面的优越性，又能反映实际问题的确定和不确定性，有益于提高农田高效节水灌溉项目后评价精度。

1 集对分析与可拓学耦合方法

1.1 原理与评价步骤

基于可拓学与集对分析耦合的评价方法基本原理，把描述或评价的对象、各特征和对象关于特征的量值组成一个整体—物元来研究，对待评价样本与标准集构成的集对展开同异反分析可拓关联函数值，据关联度的大小来定量描述各种特征参数与所研究对象的从属关系。

1.1.1 基于集对分析的可拓综合评价实际步骤

（1）确定研究对象的评价指标和评价标准，以建立衡量条件集M={M1，M2，…，Mn}，其中，Mi=（Ci，Vi）为特征元，Vi为特征Ci的量值域，进而构建相应的集对。

（2）建立可拓学论域的集对，计算其联系隶属度。

（3）结合权重计算待判样本对各特征元相应类别Nj的集成联系隶属度值。

（4）按各等级的联系隶属度大小评定等级。

1.1.2 模型构建

对于评价问题，设N为N1，N2，…，Nk，…，其中Nk（k=1，2，…，K）为所有类别（分级）的全体，Cj为第j（j=1，2，…，m）个特征（评价指标），vij为事物Nk关于指标Cj的量值，按物元概念可知，级别k评价指标值可用物元表示为同征物元Rk，如式（1）：

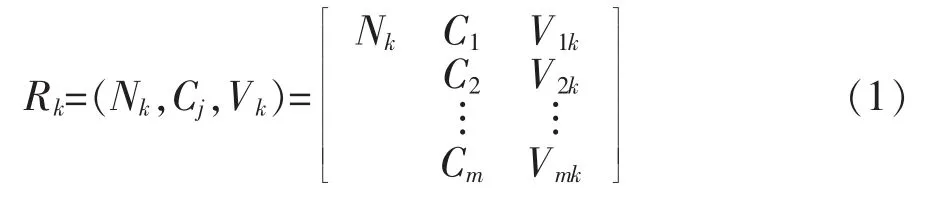
式中 Vk=（ajk，bjk）为Nk关于特征Ci所规定的量值范围，其中ajk为特征Ci的最小值；bjk为特征Ci的最大值。则经典域Rk由评价等级指标的同征物元体构成，即

评价指标的节域Rm可表达为：

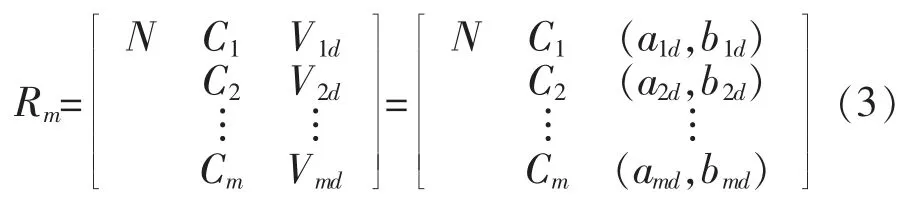
式中 N为评价对象的全部等级；（a1d，b1d）为评价指标Cj在某条件下所取的量值范围。

类似，相应的待评价样本整体的同征物元体RP（p=1，2，3，…，P）为：

基于可拓集合与集对同异反关系可知，若样本j指标落入讨论等级标准k（k=1，2，…，K）内，则其与标准等级k的关系为同，讨论等级构成的可拓集合标准正域X0=（Fj，k，Fj，k+1）内，则相应的联系隶属度计算模型如式（5）：

式中 Fj，k和Fj，k+1分别为等级界限值；μk（xij）为待样本i对讨论等级k中j指标构成的标准正域的联系隶属度。

若第i样本j指标值落在讨论等级标准k的相邻等级k-1（k＞2）或k+1内，且还在相应的过渡正域X1=（Fj，k-1，Fj，k）或X2=（Fj，k+1，Fj，k+2）内，则其与标准等级k的关系为差异，则相应的联系隶属度计算模型如式（6）～式（8）：

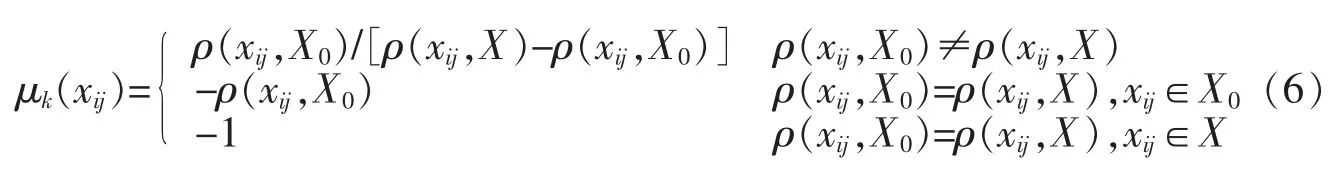
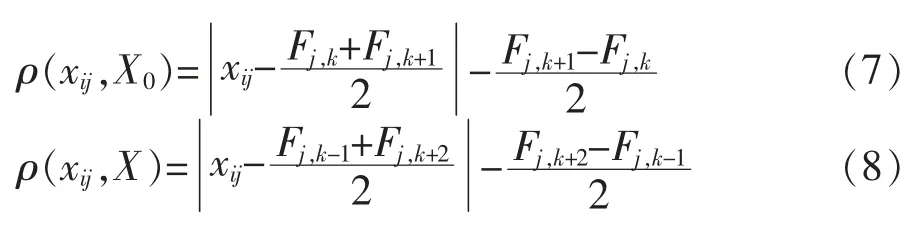
式中 Fj，k-1和Fj，k+2为等级界限值；ρ（xij，X）和ρ（xij，X0）为样本i的实测值与讨论等级k中j指标标准构成的可拓正域和标准正域的距。

若样本j指标不在讨论等级k构成可拓集合的正域X=（Fj，k-1，Fj，k+2）内，而落入讨论等级标准k的相邻等级k-2或k+2（k＞2）内或不在任何标准等级内，即在讨论等级构成的可拓集合负域Y内，则其与讨论标准等级k的关系为对立，其联系隶属度如式（9）：

结合评价指标权重，可求得相应的联系隶属度μk（p），相应计算模型如式（10）：

式中 ωj为指标权重。

由式（10）求得集成隶属度越大，说明其与某等级集合的接近程度越好，即相应的评定准则如式（11）：

式中 k为确定的评价等级。

其节水灌溉流程如图1。

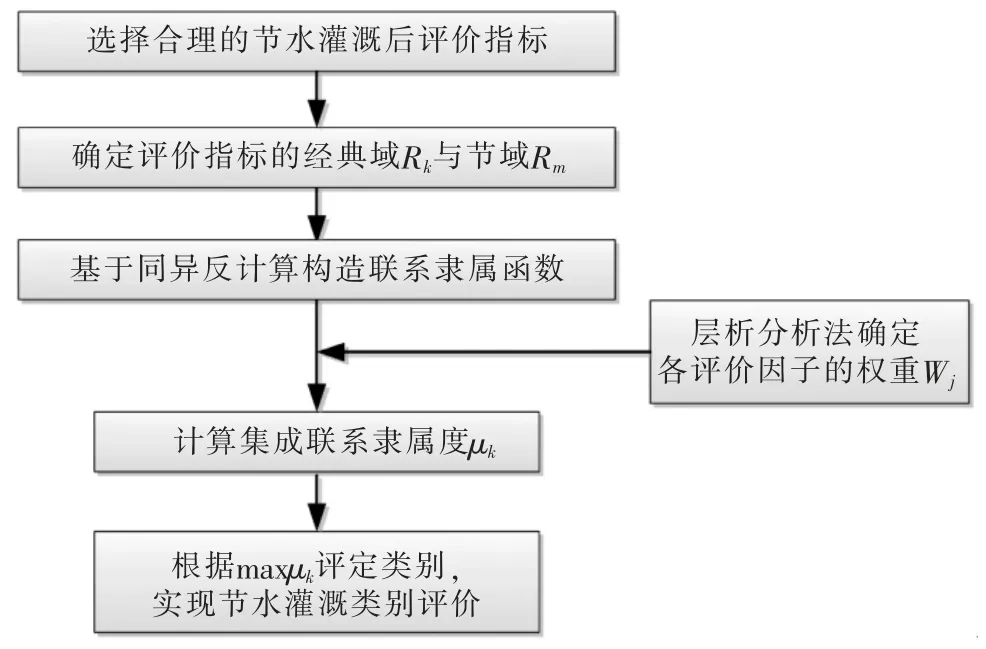
图1 节水灌溉项目集对分析与可拓评价

1.2 评价指标选取

基于国家GB/T30949—2014《节水灌溉工程项目后评价规范》、 已有研究成果和文献资料，选用投资完成率（C1）、工程完成率（C2）、经济内部收益率（C3）、灌溉水利用系数（C4）、节水率（C5）、亩均增产量（C6）、省工率（C7）、农民人均收入（C8）、减少贫困人口（C9）9个指标。结合山西省汾阳市、运城市、临汾市、吕梁市和晋中市节水灌溉工程项目的数据，将工程建设效果后评价的指标标准分为优（Ⅰ）、良（Ⅱ）、中等（Ⅲ）、一般（Ⅳ）、差（V）5 个等级。 具体分类标准取值范围如表1，样本实测值如表2。

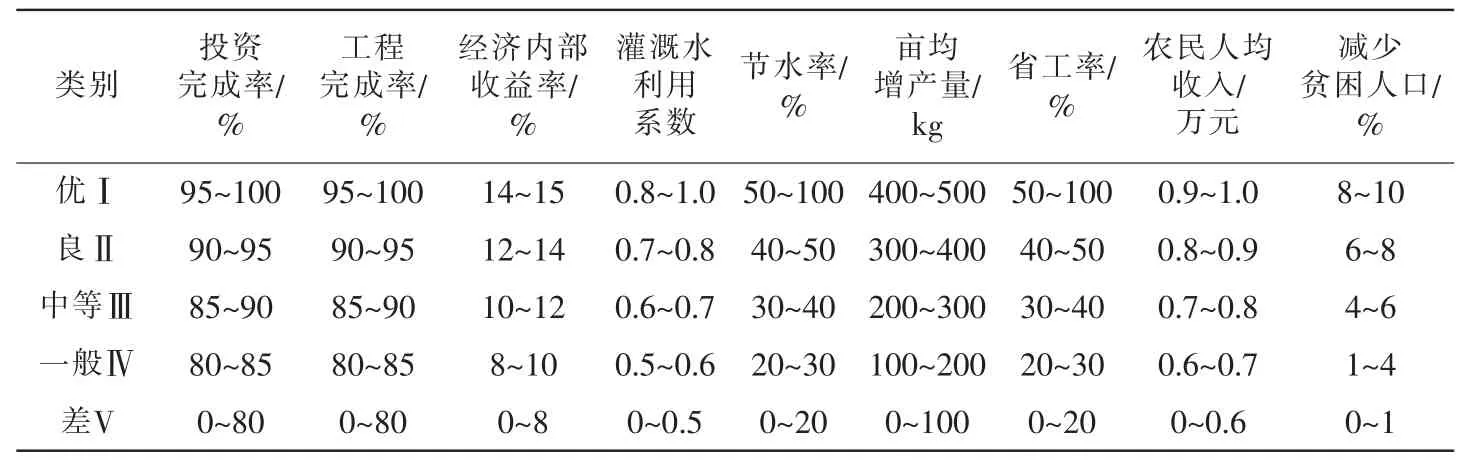
表1 评价指标分类标准

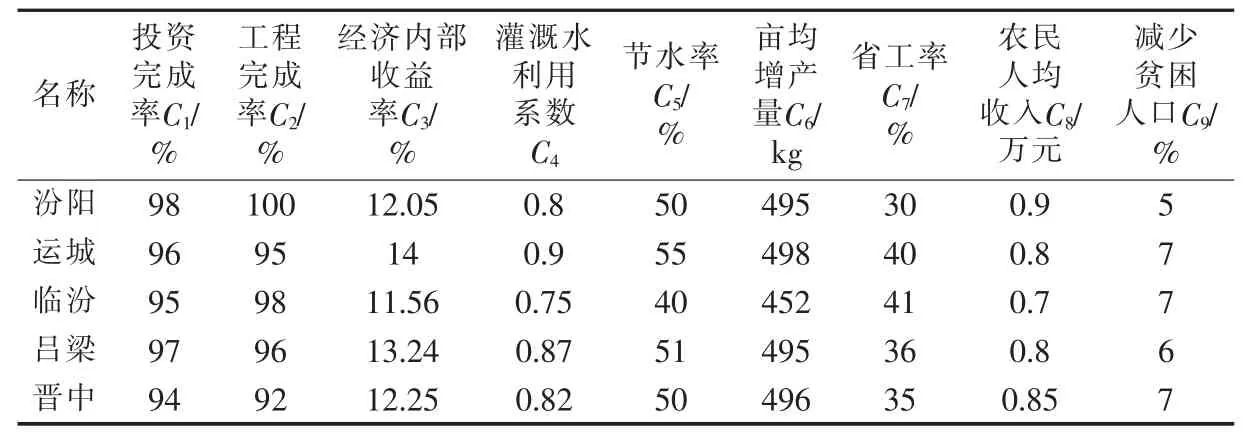
表2 样本实测值

可用同征物元体RK和节域Rm描述为：

根据实测值构成待评同征物元体：

基于集对分析与可拓学耦合方法进行评价，结果如表3。

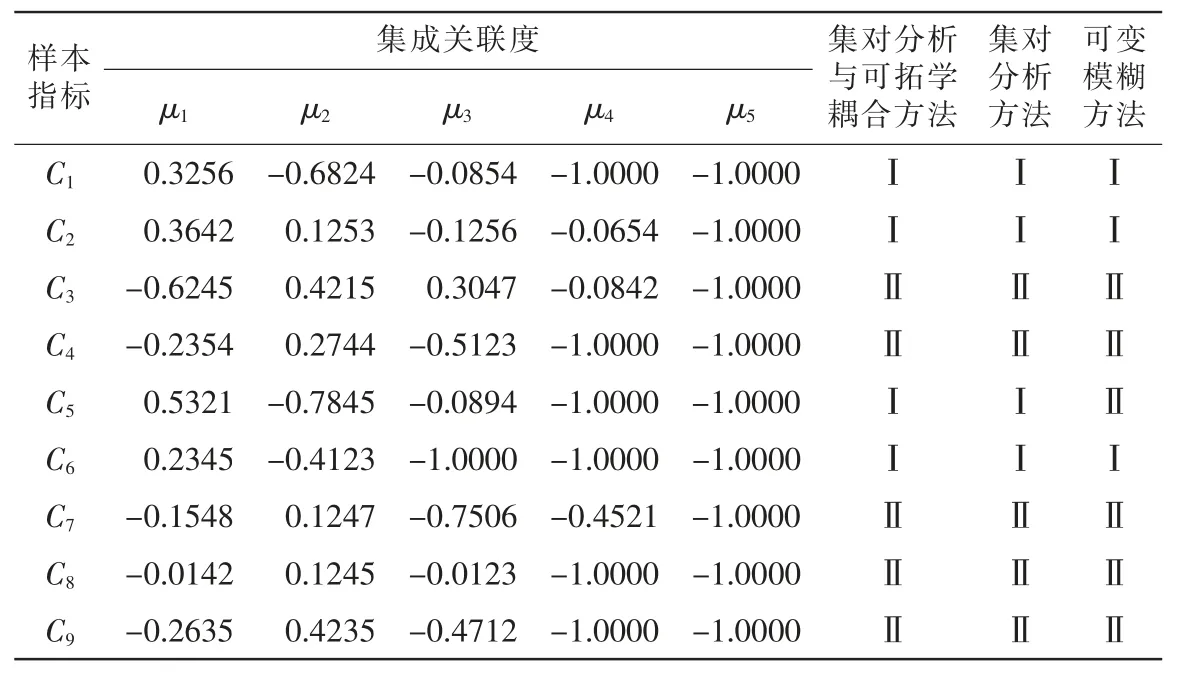
表3 集对与可拓综合评价结果

表3的结果显示基于集对—可拓综合评价的方法能有效地应用于节水灌溉项目后评价中。

2 结语

（1）采用集对分析与可拓学耦合分析方法，对山西省节水灌溉项目进行后评价，并与其他方法的评价结果进行比较，从表3可见，基于集对分析与可拓学耦合方法的评价结果是有效的，符合实际情况。

（2）利用可拓理论在计算关联度方面的优越性，有益于节水灌溉的项目评价，且分析思路清晰，计算简单。