混合单频激励下连续扫描激光多普勒振动测试*
李 繁, 臧朝平, 张 忠
(1.南京航空航天大学能源与动力学院 南京,210016) (2.北京强度环境研究所 北京,100076)
引 言
试验模态分析是了解和掌握结构动力学特性、实现结构优化设计和动力学模型修正的重要手段[1]。基于传统加速度传感器的结构振动模态测试,因传感器附加质量而影响测试结果准确性,并且由于布置传感器或测点数目有限而导致测点空间分辨率低及测试信息不完备。近年来发展的扫描激光多普勒振动测试技术(scanning laser Doppler vibrometry,简称SLDV)因其非接触测试和测试便捷等优点而被广泛使用[2]。SLDV测试的发展已经较为成熟,可以有效地测试结构频响函数,实现结构固有频率、阻尼比及模态振型的准确获取。虽然SLDV测试可以在一定程度上提高测点的密集程度,但并未从本质上解决测点分辨率低的问题[3]。
在此基础上,研究人员提出了连续扫描激光多普勒振动测试技术(continuous scanning laser Doppler Vibrometry,简称CSLDV)。CSLDV测试通过控制激光点在试验件表面以连续运动方式采集振动信号[4-6],得到试验件测点密集的工作变形(operational deflection shape,简称ODS)。CSLDV在国外起步早,实现了如正弦速度和恒速线扫描对梁、板、盘及圆柱等结构的ODS测试[7-9]。陈强等[10]实现了实际结构的CSLDV测试及ODS提取。
以往的测试方法基本是对结构施加单频正弦激励,研究者也探索了不同激励形式下的CSLDV测试。Stanbridge等[11]描述了脉冲激励下CSLDV测试的基本理论与过程。Allen等[12]研究了脉冲激励下CSLDV测试方法,实现了通过1次测试获取结构多阶模态参数的连续扫描测试方法。但是脉冲激励下的CSLDV测试一般存在高频激励能量低、系统振动衰减过快等缺陷。笔者提出一种混合单频激励下激光连续扫描的振动测试方法,并以悬臂欧拉-伯努利梁模型对混合单频激励下CSLDV测试进行仿真,最后通过梁结构的试验验证了该方法的有效性和可行性。
1 混合单频激励下连续扫描激光测振方法
1.1 问题的提出
单频正弦稳态激励下连续扫描激光多普勒振动测试,依次选取通过单点频响函数测试得到的各阶固有频率作为激励频率,完成各频率点下结构工作的变形测量[13]。
混合单频激励是使用含有多阶固有频率成分的激励信号对结构进行稳态激励,同时激发多阶模态进行CSLDV测试,可以实现多个频率点下工作变形的同时测量,提高了CSLDV测试的效率,其示意图如图 1所示。
1.2 单频正弦激励下结构工作变形测试方法
多自由度黏性阻尼振动系统运动微分方程为
(1)
其中:F为简谐力,F=F0eiωt。
方程的特解即系统简谐激励下的稳态运动为
X*=Bsin(ωt+φ)
(2)
系统受迫响应为
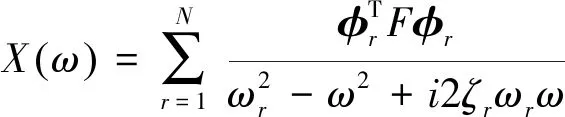
(3)
其中:φr为第r阶模态振型;ωr和ζr分别为第r阶固有频率和阻尼比。
当激励频率为r阶固有频率时,系统受迫响应以r阶模态振动为主,可认为该频率下的ODS为r阶模态振型,这是激光连续扫描测试的基础。
假设结构振型连续,可用P阶多项式拟合,即
(4)
激光测试点以频率Ω的正弦运动扫描结构表面,为方便公式推导与数据处理,将结构空间域归一化为区间[-1,1],因此激光扫描路径为
x=cos(Ωt+β)
(5)
将式(5)带入式(4)可得
(6)
利用三角函数公式将式(6)展开可得
(7)
由式(7)可以看出,正弦扫描CSLDV测试信号由固有频率ωr及其边带频率(ωr±nΩ)组成,根据边带谱幅值,可以求解ODS。
1.3 混合单频激励下结构工作变形测试方法
在混合单频激励下,结构同时受到N个固有频率的简谐激励作用,根据线性系统的模态叠加原理,结构此时某一位置的振动响应可表示为
(8)
其中:N为模态阶数;P为拟合阶次;Vn为多项式系数。
同样,激光测试点仍以频率Ω的正弦运动扫描结构,激光扫描路径由式(5)描述,将式(5)带入式(8)可得
(9)
利用三角函数公式展开可得
(10)
由此可见,混合单频激励下, CSLDV测试信号是由N个固有频率ωr(r=1,2,…,N)及其各个固有频率的边带频率(ωr±nΩ)(r=1,2,…,N)组成,根据各阶固有频率的边带谱幅值,可以求解各阶固有频率下对应的工作变形。
2 仿真分析
2.1 单频正弦激励下结构工作变形测试仿真
笔者选用欧拉-伯努利梁进行仿真测试,梁的材料与几何参数如表1所示,前3阶模态参数如图2所示。

表1 悬臂梁参数
单频激励下CSLDV测试信号实际上是由激光扫描路径上结构振型幅值调制的谐波信号。以悬臂梁第2阶为例,其CSLDV测试的激励和响应时域信号与频谱图分别如图 3和图 4所示,图中为1个周期内的测试信号,即激光从固支端扫描到自由端、再回到固支端的过程。

图2 悬臂梁前3阶模态参数

图3 单频激励CSLDV激励信号

图4 单频激励CSLDV响应信号
既然单频CSLDV测试信号由振型调制,则可以从时域角度,通过滤波提取信号包络得到ODS,这是提取CSLDV测试ODS的一种方法,但该方法只能获得扫描路径上的ODS。
由图 4可以看出,边带谱关于激励频率对称,选取一边得到边带系数矩阵Ar
Ar=[Ar0Ar1Ar2…Arn]
(11)
继而得到多项式系数矩阵Vr,其转化关系为
(12)
其中转换矩阵为
(13)
以第2阶为例,取4阶边带,Tr为5×5矩阵

(14)
将得到的多项式系数矩阵Vr代入式(4)中,即可通过多项式拟合得到ODS,这是提取CSLDV测试ODS的另一种方法,一般称此过程为工作变形解调。该方法通过拟合,可以方便准确地获得测试表面任意一点的ODS。
2.2 混合单频正弦激励下结构工作变形测试仿真
根据模态叠加原理,线性系统在混合单频激励下的响应为对应频率下响应之和,以悬臂梁前3阶为例,混合单频激励CSLDV测试的激励和响应时域信号与频谱图分别如图 5和图 6所示。可以看出,混合单频激励下CSLDV测试响应信号为多阶响应叠加,难以通过包络提取获得ODS;而混合单频激励下频谱图虽然同样包含多阶频率成分,但每阶边带谱在频域下相对独立,并与单频激励下边带谱一致,因此可通过多项式拟合方法获取各阶ODS。

图5 合单频激励CSLDV激励信号
以第2种方法分别解调的悬臂梁前3阶ODS与仿真模态振型对比如图7所示,可以看出,解调ODS与仿真模态振型一致,说明混合单频激励下CSLDV测试可以获取线性系统的各阶工作变形,从理论上验证了测试方法的有效性。

图6 混合单频激励CSLDV响应信号

图7 仿真测试结果
3 试验验证
3.1 SLDV测试
SLDV测试将激光速度传感器代替加速度传感器,测试结构频响函数,本质上还是模态测试,因激光测试没有附加质量影响,测试频响函数更加准确。进行SLDV测试目的为:a.在混合单频激励CSLDV测试之前,获取悬臂梁固有频率;b.将SLDV测试结果作为基准,作为CSLDV测试结果的评价依据。
试验基于Polytec PSV-400-3D 扫描式激光测振仪、National Instruments PXI和LabView来实现。NI LabView用于实现测试程序的开发,包括激光路径和激励信号的计算;NI PXI用于激光控制路径、激励信号的模拟输出和测试信号采集。试验装置如图8所示,测试中对梁布置15个测点,线性扫频激励,分析频率为600 Hz。混合单频激励通过激振器实现,获取了梁的前3阶模态频率,如表2所示。

图8 试验装置

表2 悬臂梁的前3阶模态频率
3.2 CSLDV测试
根据SLDV测试的前3阶固有频率,采用混合单频激励对悬臂梁进行连续扫描激光测试,激励信号为前3阶固有频率的叠加。激光扫描频率为5 Hz,采样频率为8 192 Hz,测试时间为4 s。振动速度测试信号如图9所示,测试信号频谱如图10所示。
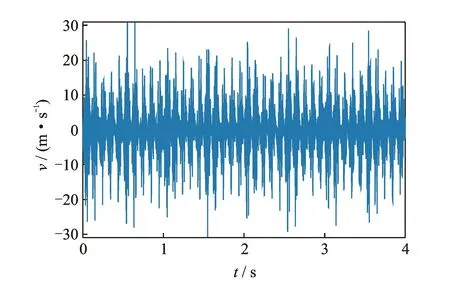
图9 振动速度测试信号
测试前3阶边带谱局部放大如图11~13所示,可以看出边带谱明显,测试信噪比高。每阶边带谱关于激励频率对称,各阶边带谱相对独立,互不影响,与仿真测试结果一致,可以利用边带谱幅值拟合测试ODS。对比第2阶仿真测试与实际测试边带谱发现,两边带谱基本一致,即测试提取ODS与仿真一致,说明了测试仿真的有效性和可行性。
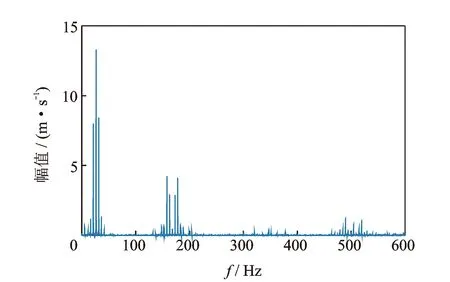
图10 测试信号频谱

图11 第1阶边带谱
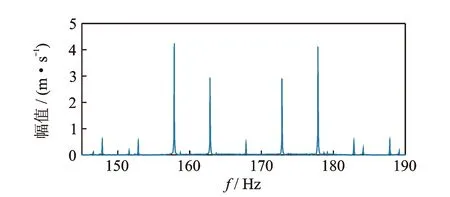
图12 第2阶边带谱

图13 第3阶边带谱
3.3 结果对比与讨论
解调出CSLDV测试ODS,并与SLDV测试结果进行对比,如图14~图16所示。可以看出,CSLDV测试与SLDV测试结果一致,3阶模态置信准则(modal assurance criterion,简称MAC)值均在0.99以上,CSLDV测试与SLDV测试其他参数对比如表3所示。可以看出, CSLDV测试具有很高的测试精度,并且在短时间内可以获得测点密集的振型数据,具有很高的测试效率,弥补了SLDV测试的不足。

图14 第1阶测试结果对比
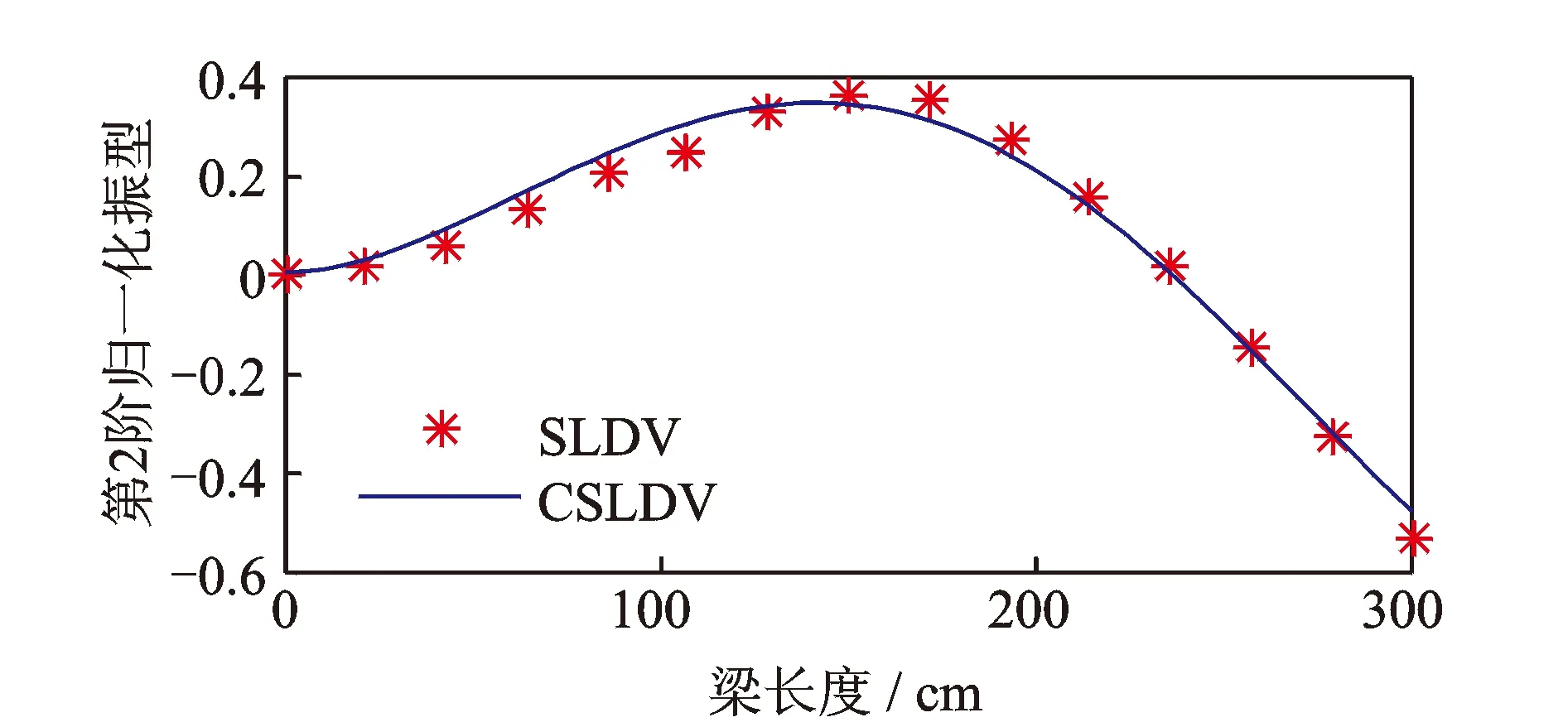
图15 第2阶测试结果对比
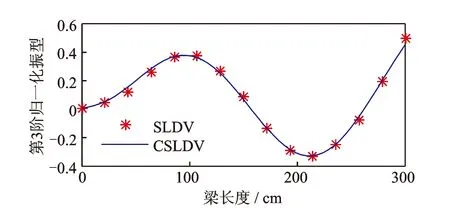
图16 第3阶测试结果对比

表3 CSLDV测试与SLDV测试参数对比
为方便描述,这里仅选取了梁的前3阶模态。事实上,此方法同时适用于更高阶的模态测试。
测试时激光扫描频率的选取与被测结构的各阶模态密集程度和阻尼特性相关。当相邻的两阶模态比较接近时,可以减小扫描频率,以避免各阶边带谱会发生重叠和交叉;当两阶模态过于接近时,产生重叠和交叉的各阶边带谱需要人为辨识,给分析带来困难,并影响到分析结果。对于同一阶模态,当激光扫描频率较小时,边带比较靠近,由于频谱分析泄漏的影响,同样会产生边带之间互相叠加从而影响其幅值,幅值较小的边带也可能会被幅值较大的边带所掩盖,进一步影响数据处理。图17给出了分别采用扫描为0.05和0.3 Hz、仿真测试刻意引入非整周期采样时,第1阶模态的边带谱变化,显然0.05 Hz扫描频率不可取。因此,在实际测试中,可通过尝试性的试验,选取使得各边带谱明显区分的扫描频率。

图17 扫描频率对边带谱的影响
4 结束语
研究了混合单频激励下连续扫描激光多普勒振动测试方法和原理。以梁结构为例,进行了仿真和试验测试分析。与SLDV测试进行了对比,结果表明,混合单频激励下连续扫描激光测试方法具有测试精度高、效率高、振型数据空间分辨率高的特点,验证了该方法的可行性和有效性。

