列车车轮多边形磨损及其噪音研究综述*
李彦夫, 门天立
(清华大学工业工程系 北京,100084)
引 言
随着世界经济的全球化发展、社会分工的全球化进程加快以及人们物质和文化生活的不断进步,铁路交通方式也发生了质的飞跃。1964年,日本的新干线标志着高速铁路时代拉开了帷幕。欧洲铁路局对高铁的定义为:在原有线路中,列车时速超过200 km/h或者新线路上列车时速超过250 km/h的铁路系统[1-2]。
随着高铁速度的不断提升,高速铁路的安全性和可靠性面临了挑战。1998年6月3日,德国发生高速城际列车(intercity-express,简称ICE)脱轨事故[3],而导致事故的直接原因只是因为一个车轮的钢材破损、剥离。从2008年开通京津线以来,中国的高铁开始快速发展。截至2017年末,中国高速铁路的运营总里程已超过25 000 km,超过了世界高速铁路运营总里程的2/3[4]。与欧洲不同,中国的高速铁路贯穿中国东西和南北,沿路环境和地势复杂,且中国部分高铁的单次运行里程很长,拥有世界上里程最长的高速铁路线路——京广高铁,长度超过2 000 km。因此,对高速铁路的可靠性和安全性有了更高的要求。
高速动车组轮对的车轮多边形磨损是影响其安全可靠性的一个关键性问题。因高速动车组的车轮多边形磨损可能导致轮轨系统的剧烈振动,对轨道和重要的车辆部件造成严重危害。其引起的高频高幅振动以及滚动噪音,也会影响乘客的安全及乘坐舒适度[5]。
1 车轮非圆化相关概念和定义
车辆非圆化磨损主要分为局部非圆化磨损和全周非圆化磨损。其中局部非圆化磨损主要包括扁疤、剥离、脱层等由于局部制动热损伤或是解除疲劳导致的磨损,主要出现在胎面的局部。全周非圆化磨损则是车轮面大部分区域均出现不同程度的磨损,又分为周期性非圆化和非周期性非圆化。全周非圆化的机理尚未探明,本研究针对的是周期性非圆化磨损。
周期性非圆化磨损又称为多边形磨损,是沿整个车轮圆周方向的磨耗。呈现周期性非圆化磨损的车轮,其半径沿着圆周方向发生周期性变化[6]。圆周上周期的数目又称为多边形阶数,偏心轮称为1阶多边形,椭圆为2阶多边形,三角形为3阶多边形,高阶多边形以此类推,如图1所示。
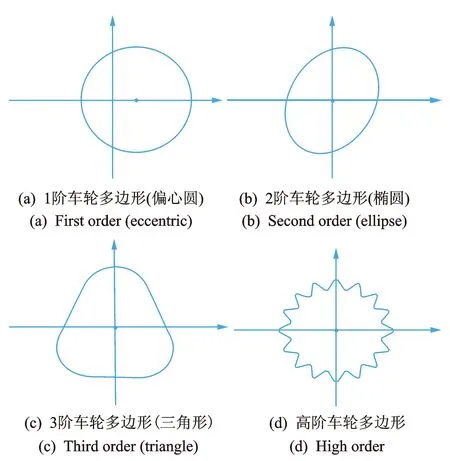
图1 车轮多边形阶次示意图
通常可以对车轮的粗糙度进行傅里叶分析,进而来描述车轮的多边形阶次。车轮多边形的波长定义为
(1)
其中:noor为多边形磨耗阶数;r为车轮半径。
当列车的车速为v时,由于车轮的多边形磨损导致的车轮自激振动频率为
foor=v/λn
(2)
车轮多边形磨损通常同时存在多个不同阶次的多边形,其波幅比例不同[6]。车轮在某处的波幅指的是该处车轮的轮径与车轮平均轮径之差。车轮的多边形磨损程度可以表示为
(3)

初始的不规则型面可以用各阶多边形磨损的粗糙程度所对应的正弦函数之和来表示
(4)
其中:an为n阶多边形磨损所对应的粗糙度幅度大小;λn为第n阶多边形磨损的波长;ψn为根据实际测量情况,对各阶粗糙度分布函数的相对位置进行修正的初相位。
(5)
其中:Lwn为第n阶多边形磨损所对应的粗糙程度。
Lwn可以根据车轮的粗糙度数据,通过谐波分析获取。
笔者收集到某列车车轮表面粗糙度阶次图,如图2所示。可以看出,该列车在20阶次时的粗糙度水平出现峰值。
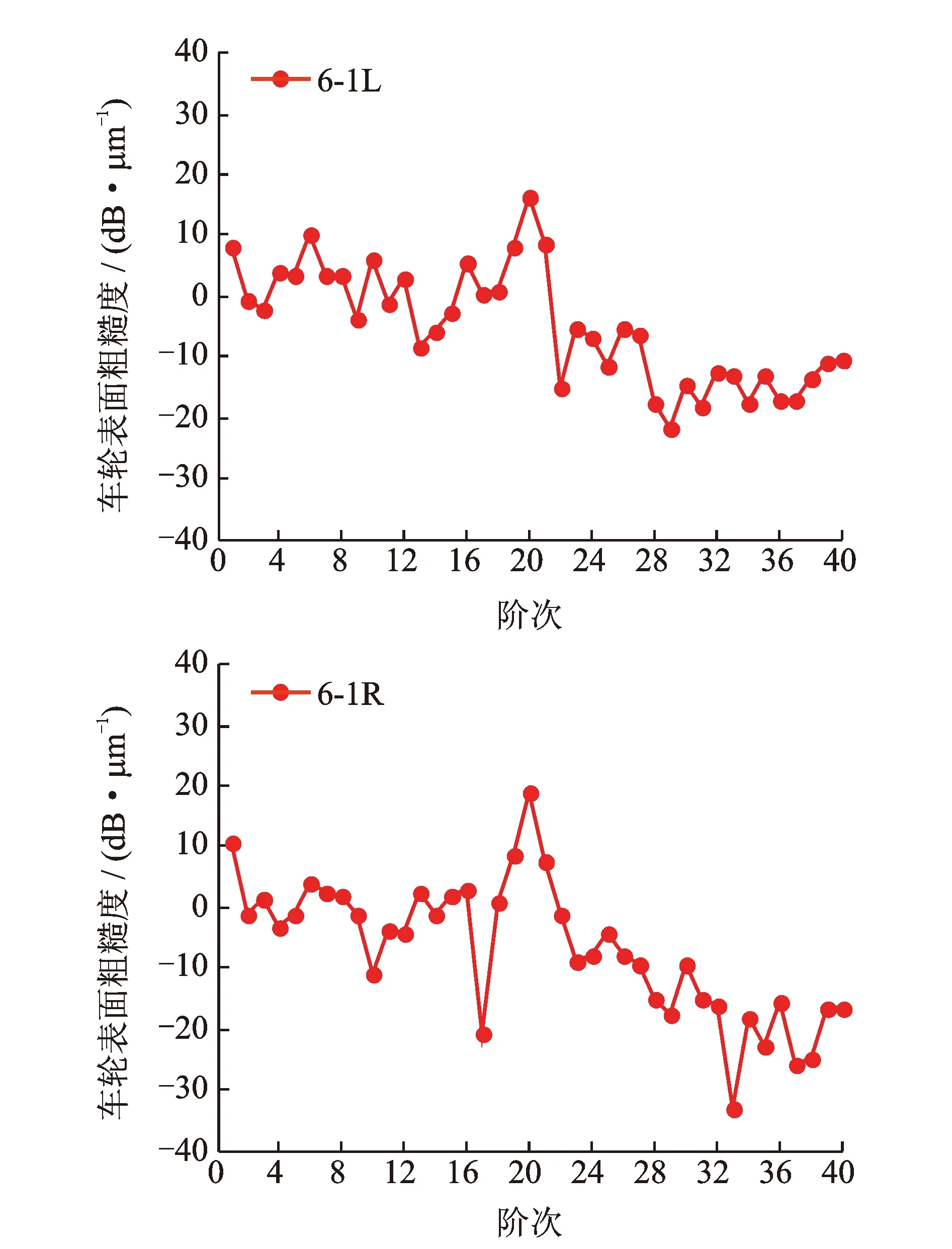
图2 某车厢车轮的测试结果
2 研究现状
2.1 车轮多边形磨损的相关研究
轨道列车车轮非圆化磨损的研究主要集中在3个方面:a.车轮非圆化对轮轨系统动力学的影响;b.车轮多边形磨损产生和发展机理;c.车轮非圆化检测和预测。其中,第3部分的检测和预测需要大量运行数据的支撑,虽然目前研究尚少,但铁路部门掌握了大量运行数据,且对车轮非圆化实时检测和预测有很大需求,所以笔者主要侧重于车轮非圆化实时监测和预测部分。
2.1.1 车轮多边形磨损对轮轨系统动力学的影响
车轮多边形磨损会导致车轮和轨道产生较大的冲击载荷,进而引起车轮和轨道部分器件受损。国内外对于车轮多边形磨损的动力学影响主要从实验和数值模拟两方面着手。实验方面主要是对多边形磨损所导致的冲击载荷的检测。Higgs等[7]设计了用于测出冲击载荷的轮对,可以测出3个方向的轮轨冲击载荷。Kalay等[8]运用应变传感仪进行冲击载荷检测,研究车速、非圆化波长和波幅对于冲击载荷的影响。文献[5]提出可以基于聚偏氟乙烯(polyvinylidene fluoride,简称PVDF)压电传感技术来测出轮轨冲击载荷。
另一方面是对动力学数值进行模拟研究。Newton等[9]建立了轨道弹性梁模型,研究车轮非圆化造成的轮轨冲击载荷。Jenkins等[10]提出了非圆化对轮轨系统动力学的影响,建立了刚性轮轨耦合模型。Ahlbeck等[11]建模分析了不同型面的轮轨造成的冲击载荷。Nielsen等[12]对多边形磨损的力学数值模拟做了综述。翟婉明[13]把车辆和轨道耦合进行动力学分析,发现在轮轨系统中,车轮非圆化幅值和车辆速度对轮轨冲击载荷有重要影响。
2.1.2 车轮多边形磨损产生和发展机理
多边形磨损产生的原因主要有以下几个方面。
1) 轮组成型过程造成后续多边形磨损。Pallgen[14]在研究列车多边形磨损问题时发现,新车轮在运行一段时间后会出现3阶的车轮多边形,这是由于制造过程中的三角爪车轮固定方式导致的。刘佳[15]提出,高速列车或者钢轨的初始不平顺会导致车辆系统在较宽频段出现谐振,进而引起车辆共振,加快车轮多边形磨耗的出现。
2) 车轮镟修工艺(不落轮镟修)导致车轮出现多边形磨损[16]。宋春元等[17]调查了我国车辆镟修工艺,发现目前我国采用不落轮镟修,采用驱动轮上压来定位,而不是中心定位,无法完全消除车轮多边形,如图3所示。
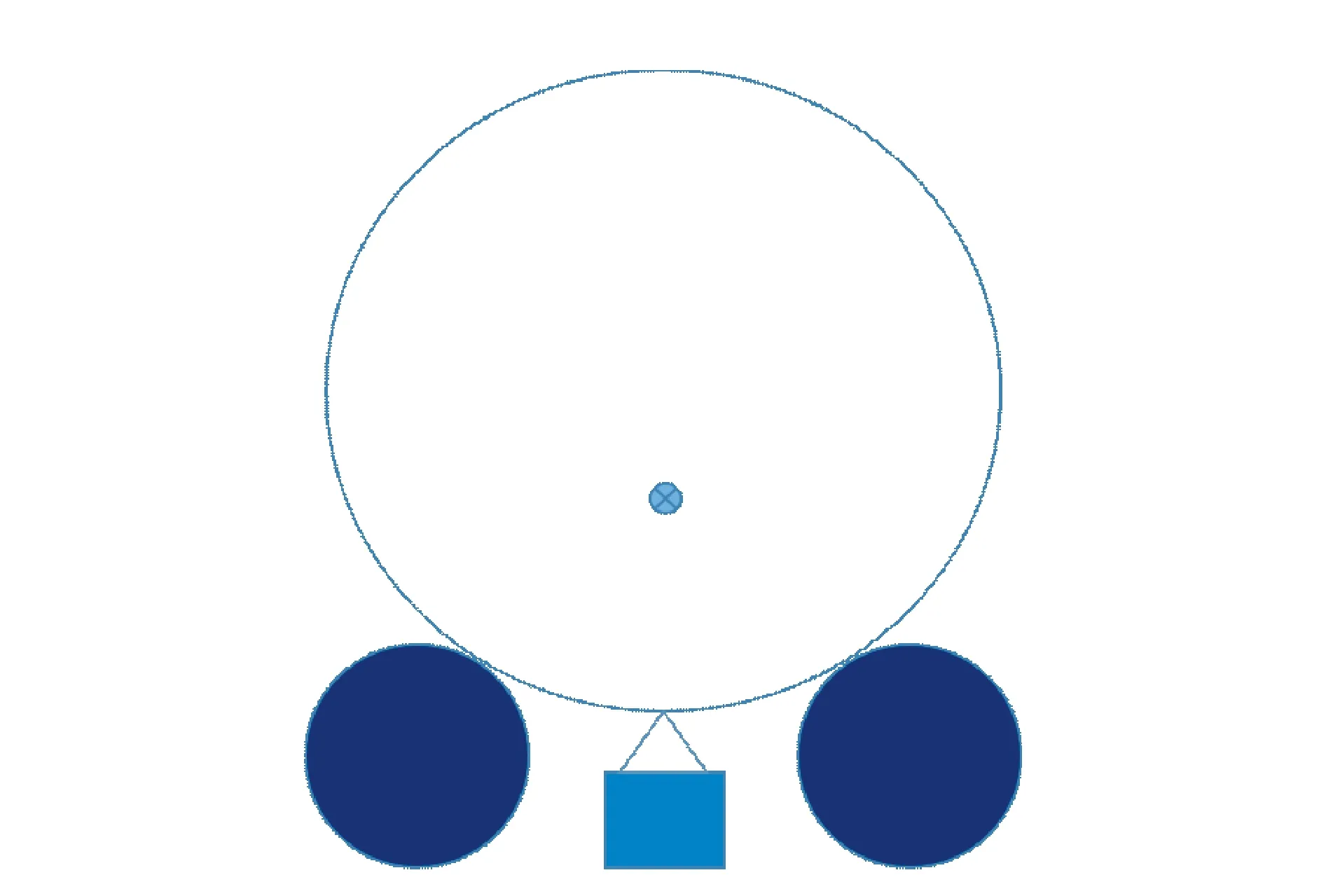
图3 车轮镟修示意图
3) 由轮对的1阶弯曲振动导致的车轮多边形磨损。Jin等[5]发现,地铁轮对的1阶弯曲振动频率与地铁的9阶多边形磨损所引起的激振频率很接近,初步得出轮对的1阶弯曲振动导致多边形问题这一结论。
4) 由轮轨表面的粗糙度引起的轮轴共振,进而导致车轮与轨道的摩擦功变化,从而导致多边形问题[18]。孙海荣等[19]利用大量列车运行及维护的历史数据,发现在首尾车轴处车轮的多边形磨损情况显著严重于其他车轴处车轮。
5) 高速时列车车轮的重心偏移导致轮轨振动,从而产生多边形磨损[20]。
6) 由于高速列车的制动,导致轮轨之间的蠕滑力饱和,从而导致多边形问题,该机理可以解释中国高速列车高阶多边形的产生[21]。陈光雄等[22]也提出,轮轨的摩擦自激振动会引起车轮非圆化磨耗。
2.1.3 车轮多边形磨损的阶次分析
列车的车轮多边形主要分布在1~20阶,不同阶次的多边形磨损产生的原因不尽相同,所产生的影响也不同,国内外学者对不同阶次的多边形磨损进行了研究。Nielsen等[23]概述了车轮非圆化的发展过程,并提出通过数值仿真来研究车轮非圆化。Morys[24]利用车辆-轨道耦合动力学模型来探究1~5阶多边形的动力响应。Johansson等[25]通过实验及数值计算,探究了波深为0.125mm的10阶车轮多边形磨损对轮轨垂向力的影响。Johansson等[26]对车轮的初始多边形磨损进行了仿真,模拟了各阶多边形磨损的演化过程,但没有考虑到动力学的影响。宋颖[27]探究了3,6,9阶次多边形磨损对轮轨动力的作用。
目前,国内外学者大多将10阶以上的车轮多边形磨损称为高阶多边形磨损,而将10阶以下的车轮多边形磨损称为高阶车轮多边形磨损。陈伟等[28]探究了高速列车中高阶多边形对车辆动力学产生的影响,通过分析数据发现,当波深相同时,车轮多边形的阶数越大,车辆蛇形失稳的临界速度越小,列车越容易出现失稳。同时将车轮多边形阶次按照轮轨垂向力的发展速度来划分,1~5阶为影响较小区域,6~9阶为平稳增长区域,10~25阶为快速增长区域。李贵宇[29]通过模拟发现,随着车轮多边形的阶数增加,车辆失稳的临界速度不断降低。从以上研究中可知,在同等其他条件下,列车的车轮多边形磨损阶次越大,对列车稳定性的危害越大,因此,高速列车出现的高阶多边形磨损应该引起足够的重视。
2.1.4 车轮多边形检测和评估
车轮的多边形检测主要分为直接和间接检测。直接检测按检测机理来分可以分为机械检测法、车轮瞬间腾空法及光电测量法等,其中机械检测法在我国使用的比较多。洪燎等[30]运用机械检测法,开发了便携式车轮多边形磨耗测试装置,可以借助滚轮和编码器进行车轮多边形的检测,如图4所示。

图4 车轮多边形直接检测方法
车轮多边形直接检测方法的可操作性和精度较高,但需要在车辆静止或者低速情况下进行,效率较低,且无法满足铁路部门关于实时监测的要求。
间接检测主要有2种方法:a.动力学检测,如Zakharov等[31]通过测试车轮与轨道间的振动加速度来检测车轮多边形磨损,戚潇月等[32]提出通过轴箱垂直加速度频谱来实现在线识别多边形阶数,并且定义了多边形车轮轴向垂直加速度系数λ来识别多边形幅值;b.通过车辆噪音来监控多边形磨损,如文献[33]指出,铁路系统车辆的噪音主要分为空气动力学噪音、集电系统噪音、轮轨噪音、桥梁结构物二次噪音和车厢内噪音,而轮轨噪音又分为曲线啸叫声、滚动噪音和冲击噪音, 车轮多边形磨损会显著加大轮轨振动,进而增大轮轨噪音。
列车噪音源识别主要有2种方法[34]:a.采用麦克风阵列进行噪音收集,把声音采集器放置在列车路过的路段近旁,通过改变采集器的阵列来获取更高的声音识别准确度,目前比较常用的有星型阵列和螺旋形阵列;b.采用不同的传感器相结合以实现噪音识别,例如通过在列车上同时布置噪音传感器和振动传感器,可以将相同频率的噪音和振动关联,从而识别、提取噪音源。王远等[35]利用了BK公司的PULSE平台测试系统,在4辆高速列车中出现异常噪音的车厢进行了噪音测试,发现车轮多边形磨损能够在噪声频谱的某些频段中被反映出来。
2.2 噪音与车轮多边形磨损之间的关系
由于车轮多边形磨损所导致的噪音主要由轮轨噪音引起,而轮轨噪音又由于轮轨振动引起,因此首先阐述车辆振动引起噪音的机理,再对车轮多边形磨损与车内噪音的关系进行综述。
2.2.1 车辆振动造成的噪音
国内外在车辆振动产生的噪音方面都有大量研究。Bender等[36]用了较为简单的无限梁弹性轨道模型,使用解析法研究轮轨系统的阻抗,但是受限于没有能精确进行轮轨粗糙度检测的设备,所以只能进行较为粗略的预测。在此基础上,Remington等[37]解释了轮轨滚动产生噪音的机理,提出了轮轨滚动噪音预测模型,把车轮和轨道的幅值随运营公里数变化的数值测出来,再通过傅里叶变换求出车轮和轨道的功率谱,在滤波之后对其功率谱进行叠加即可获得总谱。在数值模拟方面,Remington等把车轮看成刚性的,而把轨道看成连续的弹性欧拉梁。在研究噪音时又把车轮看成是点声源,而把轨道看成一系列的点声源所组成的线声源。为了分别计算车轮和轨道的噪音影响,计算了车轮和轨道的声功率,并且将其进行对比,以区分二者的噪声。最终得出的结论是:车轮产生的主要是315 Hz以下的低频噪音,而轨道产生的则主要是315 Hz以上的高频噪音。但是轮轨噪音的计算结果与实测区别很大,可能是因为没有完全反映出车轮产生的高频振动。
文献[38-39]对车轮振动产生的噪音进行了研究,对原有模型进行改进,采用弹性圆环模型来表示车轮,并且把Hertz接触刚度用于轮轨接触模型。在计算轮轨噪音时,引入了周围反射对噪音传播的影响。改进之后,模型的精度大大提高,轮轨噪音结果接近实际测量值,其中车轮产生的噪音精度有了很大提升,但是对轨道噪音的模拟仍不够精确。其轮轨滚动噪音模型主要是先测出轮轨表面的粗糙度,作为初始激励,然后经过滤波,将激励引入轮轨接触模型,分别计算车轮轴向振动、径向振动以及钢轨垂向振动,再利用振动推出噪音,三者合并求出总体的轮轨噪音。
文献[40-43]对上述模型进行了修正,除了考虑车轮和轨道的振动以外,还考虑了轨枕的振动以及噪音。设计了3类轨道模型:a.双层连续铁木辛柯梁模型,较为简单;b.2层弹性离散铁木辛柯梁模型;c.在第1类的基础上,考虑了轨道截面的变形。3类模型中:第1类最为简单易行;第2类较符合实际,计算略复杂;第3类考虑了钢轨横向振动。3类轨道模型的特点在于用铁木辛柯梁替代了之前模型中的欧拉梁,从而体现了轨道的高频成分,与实际情况更为接近。
由于铁路噪音的实验较为复杂,变量较多,又缺少理论指导,欧洲铁路研究所C163委员会组织相关成员开发了一款用来预测轮轨噪音的软件(track-wheel interaction noise software,简称TWINS)[44],该软件把轨道和车轮的不圆顺作为激励,模拟轮轨频响函数,计算出车轮噪音、钢轨噪音和轨枕噪音,并最终输出总噪音,作为预测和降低轮轨噪音、指导建立新线的重要参考。与此类似,德国的Müller-BBM公司基于Remington模型开发了RIM模型,用于预测轮轨噪音。这两款软件都假设轮轨噪音是由轮轨振动产生,把车轮以及轨道的不平度作为激励,并利用车轮和轨道的频响函数来计算轮轨噪音。
除了相关噪音预测软件的研发,国内外学者关于轮轨系统中各个元件对于噪音的贡献也有诸多研究。欧洲学者认为轮轨噪音主要由车轮振动产生,但日美学者则倾向于噪音主要由钢轨振动产生。Jones等发现[45]:在轮轨噪音中,500~2 000Hz的噪音区间中,钢轨为首要噪音源;但在3 kHz~5 kHz的噪音区间中,车轮为首要噪音源。Thompson等[46]提出:在不同的频率范围内,车轮和轨道对噪音的贡献也不同,在500Hz以下,轮轨振动产生的噪音主要来自轨枕;在1 kHz以上,轮轨产生的噪音主要来自钢轨;而更高频率的噪音则主要来自车轮。
测试列车噪音时,获得的噪音不仅是轮轨噪音,还包括其他类别的噪音。翟婉明[13]提出,高速列车的噪音源除了轮轨噪音,还包括气动噪声、集电系统噪声以及其他噪声,其中高速列车的轮轨噪声主要集中在0~4 kHz范围, 1 kHz以下的中低频噪音相对较为严重。气动噪声与列车速度密切相关,我国科研工作者对和谐号高速列车展开了噪声实地测试[47],并就轮轨噪音、气动噪音与列车时速的关系得出了重要结论:轮轨噪音与列车时速的2.6次方成正比,而气动噪音与列车时速的7次方成正比;在315 km/h以下,轮轨噪音占主导;315 km/h以上,气动噪音占主导。气动噪音的频段相对于轮轨噪音来说比较集中,主要分布在2 kHz以上的中高频段。集电系统噪音主要在列车有速度变化时出现,比如列车启动以及制动阶段。其他噪音主要包括环境噪音,跟列车所处地理位置以及天气情况等有关,这种噪音一般间断出现。
2.2.2 车辆多边形磨损造成的噪音
车轮多边形磨损造成的噪音主要是轮轨噪音。当列车时速在300~350 km/h时,气动噪音和轮轨噪音为主要的噪音来源,其中轮轨噪音主要集中在1 kHz以下的中低频段,而气动噪音则集中在2 kHz以上的中高频段。为了研究多边形磨损所造成的噪音的性质,首先阐述其机理,如图5所示。
对于1阶多边形磨损,车轮表现为偏心圆,圆周每旋转1周,轮径的变化正好为1个完整周期的简谐波。对于2阶、3阶、n阶多边形磨损,圆周每旋转1周,轮径的变化分别是偏心圆的2,3,n倍。
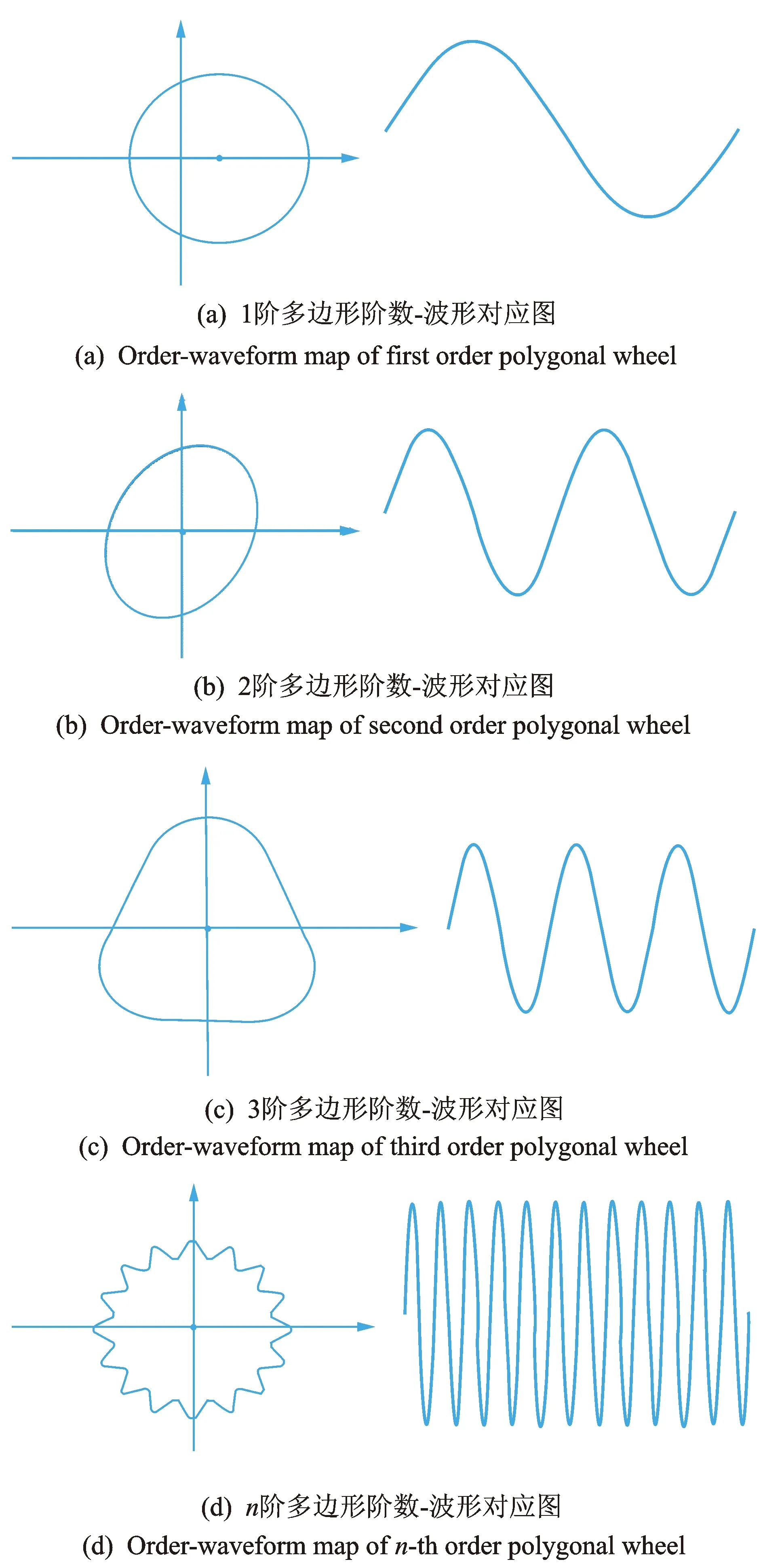
图5 多边形阶数-波形对应图
由图5可见,随着车轮多边形阶数增大,车轮多边形引起的轮轨振动频率越高。n阶多边形所引起的轮轨振动频率为
fn=Vnoor/πd
(6)
其中:fn为n阶多边形振动频率;v为列车速度;noor为多边形阶次(即为n);d为车轮轮径。
车轮出现多边形磨损后,轮轨振动会引起轮轨噪音,这也是多边形磨损所导致噪音的主要成分。
若车速为250 km/h,车轮为偏心(即多边形阶次为1),轮径为900 mm,则车轮多边形磨损造成的轮轨振动频率为f1≈24.5 Hz。当车轮为椭圆时(即多边形阶次为2),车轮多边形磨损造成的轮轨振动频率为f2≈49 Hz。当车轮为n阶多边形磨损时,其轮轨振动频率为fn=24.5nHz,即轮轨噪音主频为24.5nHz。
在一般的高铁列车上,出现频率较高的是20阶多边形磨损,若按照时速250 km/h、轮径900 mm来分析,此时的噪音主频约为f20=490 Hz,属于中低频噪音。由于列车高速行驶时所产生的气动噪音集中在2 kHz以上,因此可以通过分析噪音的声功率谱密度来预测多边形磨损。
针对多边形磨损问题的研究有很多[12,24,48]。金学松等[49]提出,列车在高速行驶时,会因轮轨不平顺而受到冲击力的作用,这种冲击会通过列车的悬架系统向上传递,从而导致车辆振动并辐射噪音,且轮轨振动的冲击也会向外辐射轮轨噪音。随着车轮多边形磨损的加重,轮轨之间冲击力会大幅增加,甚至造成车轮跳轨,此时轮轨振动所发出的噪音明显变大,车厢内噪音也随之加大。刘闯等[50]发现,镟修后的车轮会继承部分或者全部镟修前的非圆化特点,而同时期的噪声频谱可以对高阶非圆化阶次的特有频率有所反映。
韩光旭等[51]研究了车辆多边形磨损对于高速列车振动噪声的影响,对正在启用的高速列车进行了车内振动及噪音测试,并且对车轮进行粗糙度检测。通过对比车轮的多边形特征与检测的振动和噪音频谱,研究车轮多边形阶次及车轮的径跳幅值对高铁列车车内振动及噪音的影响,发现当列车以300 km/h速度运行时,车内的异常振动噪声主频在580 Hz左右,产生原因为车轮20阶多边形,噪声比正常区域大9 dB左右,振动偏大12 dB左右。同时,高阶的多边形磨损相对于低阶多边形磨损对于振动噪音的影响更大。王兴宇[52]通过量化分析,研究了多边形阶数与振动噪声频率之间的关系,发现18~20阶的多边形磨损对中频段的噪音有重要影响。文献[53]研究发现,车内噪音在300~600 Hz内很容易出现声振共振,当列车车轮的多边形磨损处于这一区间时,车辆的振动和噪音水平会大幅增大,当对车轮进行镟修之后,车内的噪音明显下降。
为了研究车辆的多边形磨损所产生的噪音与车辆部件的关系,韩光旭[54]研究了车辆系统的固有模态频率,发现所研究的列车在进行镟修之后,固有频率密集分布区的噪音频谱显著降低,降低程度大于其他频率范围的降低程度。由此可以看出,车辆系统的固有频率会影响车轮多边形磨损所产生的噪音,其原理大致推断为器件共振所致。
张捷等[55]在研究高铁车辆多边形磨损与轮轨噪音关系时进行了一系列的实验验证和数值模拟,实验包括多边形检测、在役高铁车轮的特性检测及镟修对于高铁车厢内噪音的影响。在数值模拟方面,使用了高铁轮轨噪音模拟软件(high-speed wheel-track noise software ,简称HWTNS),研究了由不均匀的车轮磨损所导致的高铁轮轨噪音。将有限元方法与统计能量分析(finite element-statistical energy analysis ,简称FE-SEA)相结合,对高铁车厢内噪音进行了建模计算,同时使用模拟方法来研究车轮多边形磨损特性(如粗糙程度、多边形阶次、多边形程度等)对于轮轨噪音以及车厢内噪音的影响。在研究车轮多边形磨损产生的噪音对车辆振动噪音的贡献大小时,比较了同一列车两节车厢,发现在粗糙度保持基本相同的前提下,多边形磨损程度大的车轮所处的车厢内测出的噪音要明显大于多边形磨损程度较低的车轮所处的车厢。该研究还得出,高铁车辆组中普遍存在的多边形磨损阶次都在19阶,导致的振动噪音在540 Hz左右,刚好是19阶多边形所引起的激振频率。
2.3 列车维修概述与多边形磨损车轮的维修策略
车轮多边形磨损产生的噪音极大影响了乘客的乘车体验,针对多边形磨损所产生的噪音问题,需要从列车的维修,尤其是车轮的镟修上着手解决。在我国,列车的维修成本一直居高不下,其中有部分原因是因为没有完备的零部件替换标准,存在过早替换的问题。
文献[56]指出,由于高速列车的生产和运营只有10年左右,缺少足够的维修研究和维修经验。目前我国所使用的维修方法主要参照欧美先进国家总结出来的维修策略,根据维修地点不同,分为1级修到5级修。为了确保列车的安全,只能减少维修周期来提高可靠性,这势必会增大维修和停机所导致的运营成本,造成不必要的浪费。国外有一些先进的修程修制,如日本高速铁路采用了先进的故障诊断系统和检测设备,以及定期预防维修制度。德国铁路自主设计ICE高铁,在制造的过程中已经考虑了维修制度,真正运用了可靠性维修理论。
在进行部件的寿命预测时,需要根据系统实际情况,结合现行修程来提出适合的寿命分布数学模型。目前主流的模型有:a.两状态模型,适用于只有工作和故障两种模态的系统;b.多状态模型,适用于在完好和失效之间存在多个模态的系统;c.比例风险模型,适用于有多个外部变量对系统联合产生作用的情况。对于不同的部件,需要使用适合的模型来进行分析[56]。
与多边形磨损相关的故障维修主要是车轮的维修与替换。在欧洲地区,以瑞典为例,列车车轮维修的标准[12]如下。
1) 如果缺陷长度在40~60 mm,或者胎面上存在一个鼓包(高度小于1 mm),则列车需要维修。如果出现了这些情况,那么列车在-10°C下的行驶速度不能超过10 km/h;在更高的温度下,行驶速度不能在15~45 km/h之间,因为在这速度范围内,列车对轨道所造成的损伤最大。
2) 如果缺陷长度超过60 mm,或者胎面上存在一个鼓包(高度大于1 mm),那么列车必须要立刻前往最近的维修站,且速度不能超过10 km/h。
车轮多边形磨损所对应的维修方式主要是车轮镟修加工处理,来恢复车轮圆度,以继续投入使用。然而,由于国内相关研究起步较晚,镟修策略多为引进国外的经验,不能完全考虑到国内复杂的地理和气候条件,因此镟修的频率比理论上需要镟修的频率要大很多;而车轮在经过不断镟修之后,踏面的直径不断减少,加速了车轮的报废,严重影响使用寿命。因此,制定合理的镟修策略对降低铁路成本至关重要[57]。
国内外关于车轮镟修的研究,主要集中于车轮踏面设计、磨损量估计以及剩余寿命预测,较少文献对车轮镟修策略进行研究[57]。Braghin等[58]对意大利的ETR500型快速客运列车车轮进行数值模拟,发现如果把镟修策略改为2×105km镟修1次,则可以把车轮的使用寿命提高1倍。孙海荣等[59]通过数据挖掘,提出一种多边形磨损预测模型,拟合效果较好,可以借助预测模型来实现提前维修。Pascual等[60]对西班牙某公司的机车车轮磨损数据进行研究,发现当轮缘厚度为27.5 mm时,通过维修使得轮缘厚度恢复到30.5 mm会使维修总成本最低。
冲击力载荷检测的出现为建立多边形磨损车轮的替换标准奠定了基础,可以不必直接测量车轮的非圆化情况,而使用机器在运行中间接检测,提高了判断的实时性。根据文献[12],北美地区对于多边形磨损车轮的更换标准发生过变化。1996年1月起,如果在运行过程中,车轮产生了超过400 kN的冲击载荷,则车轮需要被更换。允许的车轮磨损长度由50.8 mm增加到63.5 mm。笔者经过调研发现,造成超过445 kN的冲击载荷的车轮中,只有一半左右的车轮出现了肉眼可见的需要解决的缺陷,而且相比于缺陷的长度而言,缺陷的深度是一个更好的判断车轮好坏情况的指标。
文献[8]研究了不同的车轮型面,给出了经济性分析,指出如果能够基于冲击载荷提出一个合理的更换车轮的策略,就能显著降低成本。李奕璠等[61]提出了一种基于Hilbert-Huang变换来对车轮多边形磨损进行故障诊断的方法。Wu等[62]通过研究发现,列车变速行驶能够有效控制车轮多边形磨损的出现及发展。韩光旭等[63]通过实测发现,我国高铁列车普遍存在20阶多边形磨损,产生580 Hz左右振动频率,建议动车组检修单位不仅要看车轮径跳值来判断是否维修,也要制定与阶次相关的维修标准,镟修时要修正车轮的高阶多边形。
笔者在研究某列车的车轮周围噪音与车轮非圆化阶次的高阶程度的关系时,发现高阶程度和噪音主频的声压级密度近似呈现对数关系,如图6所示。

图6 某车厢各车轮主频功率谱密度-高阶程度图
由于目前能获取的车辆噪音数据和车轮多边形磨损阶次、程度数据较少,尚未验证该对数关系的可靠性,但是这一结果可以为今后的研究提供参考。
3 结束语
虽然目前在车轮多边形磨损方面有较多研究,但是对多边形磨损的机理尚未完全清楚,仍停留在验证阶段。我国对于车辆-轨道耦合动力学方面的研究已有较大成果[64]。在高铁多边形磨损与噪音的关系方面,国内外均有较多文献在研究轮轨振动所导致的噪音[34,38,46]和多边形磨损所导致的噪音[55],但还没有通过噪音来反向评估多边形磨损的文献。目前,轮轨噪声,尤其是高频轮轨噪声的研究尚未完成,特别是涉及到车轮旋转效应和轮轨噪声源分离这部分的问题,目前仍然亟待解决。不过,国际上已经有了一些较为初步的轮轨噪音预测模型以及软件,如TWINS[44],且预测效果较好。今后可进一步考证,可否通过监测车内的噪音,再辅以车轮的初始型面、轨道型面等数据,来评估或预测车轮的多边形磨损情况。
当前在高铁车辆的故障预测和维修上的研究较少,发生多边形磨损的车轮状态预测和视情维修的难题尚未得到解决,这使得高铁的运营和维修成本难以降低。高铁的安全至关重要,为了实现既保障乘客安全、又尽可能节约成本的目标,需要对多边形磨损的预测方法进行研究。另外,关于制定维修策略方面,在借鉴国外经验的同时,要结合国内复杂的地形和气候条件,制定符合我国情况的维修策略,以保障铁路车辆的安全性。

