线性回归方程常见题型剖析

■李志勤

近几年高考对相关关系以及线性回归方程的考查力度逐步增加,主要考查同学们的数据处理能力、运算能力、阅读能力,以及利用统计思想解决问题的能力。利用具有相关关系的两个变量,得到的线性回归方程可以用来预测与估计,为决策提供依据。下面通过具体例题剖析线性回归方程的常见题型。

一、相关关系的判断

例1某数学小组从医院和气象局获得2018年1月至6月每月20日的昼夜温差x(单位：℃,x≥3)和患感冒人数y(单位：人)的数据,画出如图1所示的折线图。

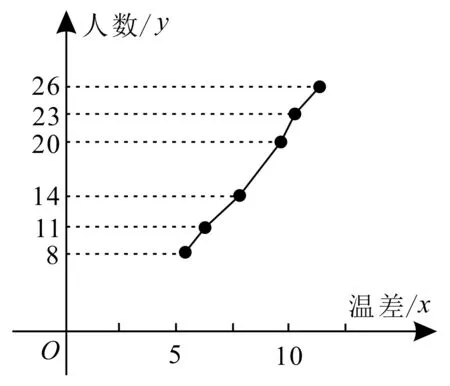
图1

(1)建立y关于x的回归方程(精确到0.01),预测2019年1月至6月昼夜温差为4℃时患感冒的人数(精确到整数)。

(2)求y与x的相关系数,并说明y与x的相关性的强弱(若r＞0.75,则认为y与x具有较强的相关性)。

分析：(1)由已知求得b与a的值,即得线性回归方程,取x=4求得y的值,可预测2019年1月至6月昼夜温差为4℃时患感冒的人数;(2)求出的值,结合b的值进一步求得r的值,可得y与x的相关性。

解：(1)由已知条件可得b=17,a=17-2.61×9.15≈-6.88,所以y关于x的线性回归方程为^y=2.61x-6.88。当x=4时,^y=2.61×4-6.88≈4。

故预测2019年1月至6月昼夜温差为4℃时患感冒的人数为4。

当r＞0时,表明两个变量正相关;当r＜0时,表明两个变量负相关;r的绝对值越接近于1,表明两个变量的线性相关性越强,r的绝对值越接近于0,表明两个变量之间几乎不存在线性相关关系。通常当|r|＞0.75时,认为两个变量有很强的线性相关性。

二、利用线性回归方程进行预测

例2已知某校5个学生期末考试数学成绩和总分年级排名如表1所示。

表1

(1)通过大量事实证明发现,一个学生的数学成绩和总分年级排名具有很强的线性相关关系,在表1是正确的前提下,用x表示数学成绩,用y表示年级排名,求y与x的回归方程。(其中b,a都取整数)

(2)在本次考试中,预计数学分数为120分的学生的年级排名大概是多少。

分析：(1)求出x,y的平均数,再求出相关系数,即可求出回归方程;(2)由x的值,可求出y的预报值。

解：(1)由表1可得(115+112+93+125+145)=118,(250+300+450+70+10)=216。

利用参考公式可得b=-9,a=1278,故y与x的回归方程为^y=-9x+1278。

(2)当x=120时,^y=198,故预计数学分数为120分的学生的年级排名大概是198。

本题考查求回归方程问题,考查函数的求值问题,属于一道常规题。利用回归直线可以由一个变量的变化推测另一个变量的变化,为决策提供依据,可见利用回归直线可以对实际问题进行分析与预测。

三、对线性回归方程性质的考查

例3在“新零售”模式的背景下,自由职业越来越流行,诸如：淘宝网店主、微商等。现调研某自由职业者的工资收入情况,记x表示该自由职业者平均每天工作的时间(单位：h),y表示平均每天工作xh的月收入(单位：千元)。x,y的对应值如表2所示。

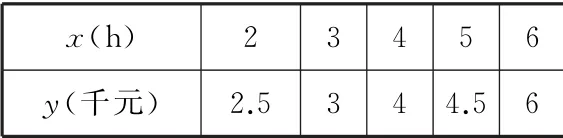
表2

假设y与x具有线性相关关系,则y关于x的线性回归方程^y=bx+a必经过点( )。

A.(3,3) B.(3,4)

C.(4,4) D.(4,5)

分析：根据所给的数据,求出x和y的平均数,得到数据的样本中心点,根据线性回归方程一定过样本中心点,即得线性回归直线一定经过的点的坐标。

解：由可得这组数据的样本中心点是(4,4)。

因为线性回归方程过样本中心点,所以线性回归方程一定过点(4,4)。应选C。

本题考查线性回归方程的性质,即线性回归方程一定过样本中心点。解答本题的关键是正确求出样本中心点,题中的运算量比较小,属于统计问题的基础题。

四、线性回归方程的交汇问题

例4某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如表3所示的数据。

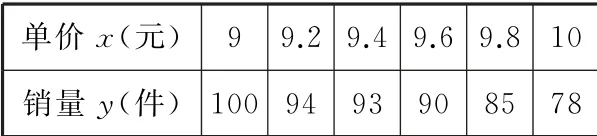
表3

(1)若销量y与单价x服从线性相关关系,求该回归直线方程。

(2)在(1)的前提下,已知该产品的成本是5元/件,问该产品如何确定单价,可使工厂获得最大利润。

参考公式：对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线方程=bx+a的斜率的最小二乘估计值为b=

分析：(1)由题意求出b与a的值,可得线性回归方程;(2)设该产品的售价为x元,工厂利润为L元,由题意可得L=(x-5)·(-20x+280)=20(x-5)(14-x),然后利用二次函数求最值。

解：(1)由题意可得则a==90+20×9.5=280。故回归直线方程为^y=-20x+280。

(2)设该产品的售价为x元,工厂利润为L元。因为当x≤5时,利润L≤0,定价不合理,所以x＞5。由^y=-20x+280＞0,可得x＜14,故5＜x＜14。

由题意可得L=(x-5)(-20x+280)=20(x-5)(14-x),根据二次函数的图像与性质可知,当x=9.5时,L取得最大值。因此为使工厂获得最大利润,该产品的单价应定为9.5元。

线性回归方程的交汇命题主要有两类：一是与概率、统计的交汇,二是与函数的交汇。解答这类问题要综合利用线性回归方程的性质求解。

五、线性回归方程在生活中的应用

例5某地随着经济的发展,居民收入逐年增长,表4所示的是该地一建设银行连续5年的储蓄存款(年底余额)。

表4

为了研究和计算的方便,工作人员将表中的数据进行了处理,t=x-2012,z=y-5,由此得到了表5。

表5

(1)求z关于t的线性回归方程。

(2)通过(1)中的方程,求出y关于x的回归方程。

(3)用所求回归方程预测到2022年年底,该地储蓄存款额可达多少?

分析：(1)由表中的数据求得,再得到b与a,即得线性回归方程;(2)将t=x-2012,z=y-5代入=1.2t-1.4,可得y关于x的回归方程;(3)利用(2)中的回归方程,令x=2022,即可求得y的值。

解：(1)由可得1.4。

本题主要考查线性回归方程的求法,考查计算能力,考查数学思想在统计中的应用。