频率分布直方图的应用举例剖析
■蒋庆富
频率分布直方图是表示和分析统计数据的重要工具,是高考考查的重点。下面总结频率分布直方图的几种常见应用,希望能帮助同学们对所学知识的巩固与提高。
一、频率分布表或频率分布直方图的应用
例1某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min)。下面是这次抽样的频率分布表(如表1)和频率分布直方图(如图1),则旅客购票用时的平均数可能落在( )。
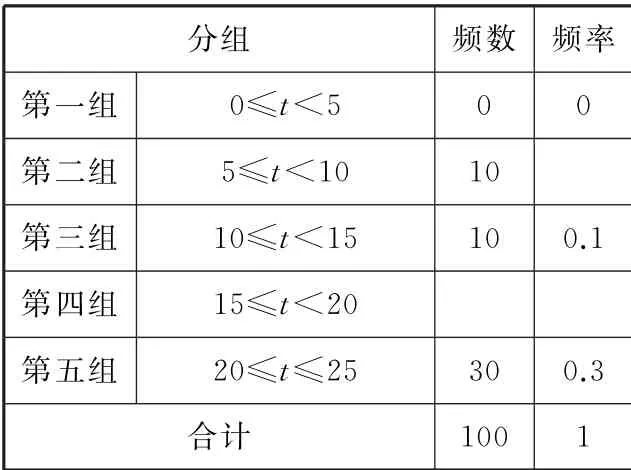
表1

图1
A.第二组 B.第三组
C.第四组 D.第五组
解:由频率分布表可得,第四组的频率为1-0.1-0.1-0.3=0.5。
由频率分布直方图可得,旅客购票用时的平均数为7.5×0.1+12.5×0.1+17.5×0.5+22.5×0.3=17.5,所以旅客购票用时的平均数落在第四组。应选C。
本题考查频率分布表和频率分布直方图的应用,考查平均数和频率的求法。解题时,先求第四组的频率,再求平均数,从而可以判断平均数落在哪个小组。
二、求频数或频率
例2某市高一数学抽样考试中,对90分及以上的成绩情况进行统计,其频率分布直方图如图2所示,若(130,140]分数段的人数为20人,则(90,110]分数段的人数为( )。
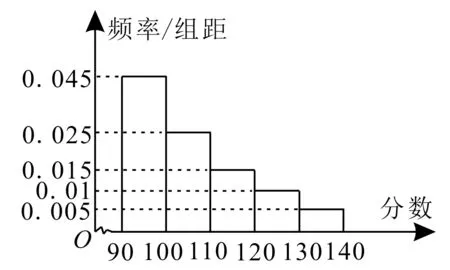
图2
A.18 B.180
C.28 D.280
解:由频率分布直方图可得(130,140]分数段的频率为0.005×10=0.05。
由(130,140]分数段的人数为20,可得
因为(90,110]分数段的频率为(0.045+0.025)×10=0.7,所以(90,110]分数段的人数为0.7×400=280。应选D。
本题考查频数的求法,考查频率分布直方图的性质,考查运算求解能力。频数表示某一项或某一组出现的次数,是直观的数量;频率是某一组在总体中所占的比例,即=频率,所以频率之和一定等于1。
三、求样本数据的平均数,中位数或众数
例3为适应新的高考改革,某校从高一开始组建了一个试验班。已知该班某次数学考试成绩的频率分布直方图如图3所示,设其成绩的众数,中位数分别为x,y,则|x-y|=( )。
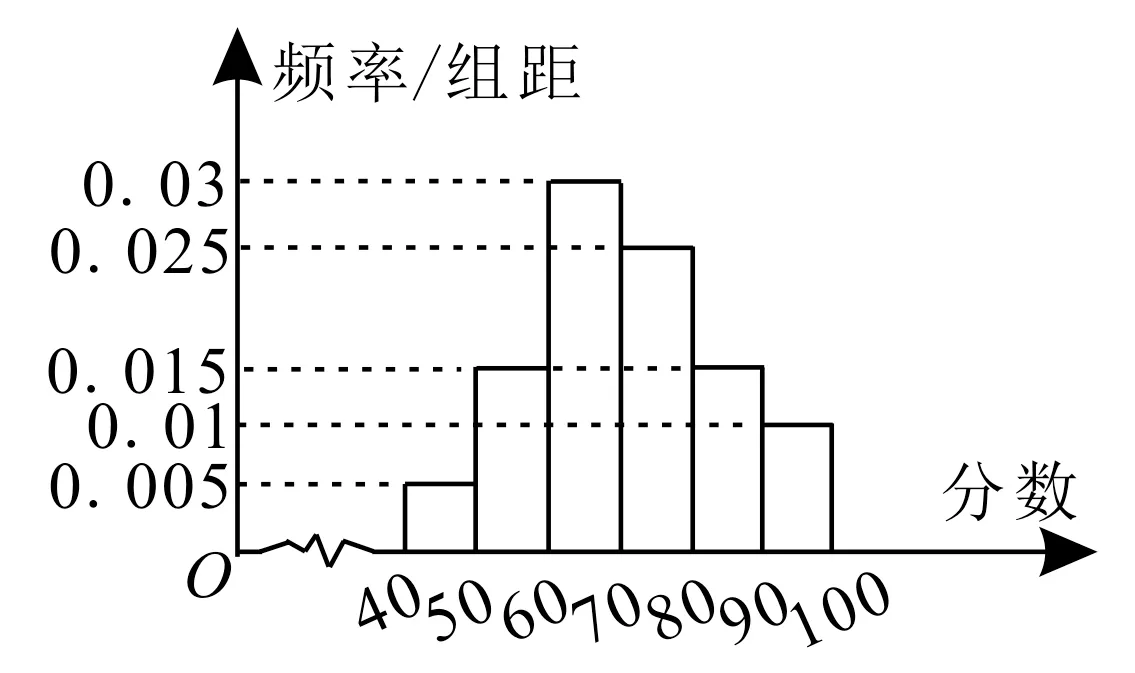
图3
A.4 B.4.5
C.5 D.5.5
解:由频率分布直方图可得众数x=
由成绩在[40,70)上的频率为(0.005+0.015+0.03)×10=0.5,可得中位数y=70,所以|x-y|=|65-70|=5。应选C。
本题考查众数,中位数的求法,考查频率分布直方图的综合应用,考查运算求解能力以及函数与方程思想。
例4据全球权威票房网站Mojo数据统计,截至2017年8月20日14时,《战狼2》国内累计票房50亿,截至目前,《战狼2》中国市场观影人次达1.4亿,这一数字也创造了全球影史“单一市场观影人次”的新纪录,为了解《战狼2》观影人的年龄分布情况,某调查小组随机统计了100个此片的观影人的年龄(他们的年龄都在区间[10,60]内),并绘制了如图4所示的频率分布直方图,则由图可知,这100人年龄的众数和平均数各等于( )。
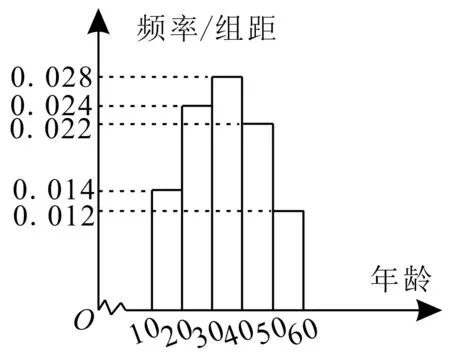
图4
A.34,38.2 B.34,32.1
C.35,34.4 D.35,45.6
解:由频率分布直方图可得第三组的频率最大,则这100人年龄的众数为35,其平均数=0.014×10×15+0.024×10×25+0.028×10×35+0.022×10×45+0.012×10×55=34.4。
故这100人年龄的众数为35,平均数为34.4。应选C。
在频率分布直方图中,众数是最高小长方形的底边中点所对应的数据,它表示样本数据的中心值;中位数是左右两边的小长方形的面积相等的底边的值;平均数等于各个小长方形的面积乘以对应小长方形底边中点的横坐标之和。
四、求频率分布直方图中小长方形的高或面积
例5已知一组样本数据被分为[10,20),[20,30),[30,40]三段,其频率分布直方图如图5所示,则从左至右第一个小长方形的面积是( )。
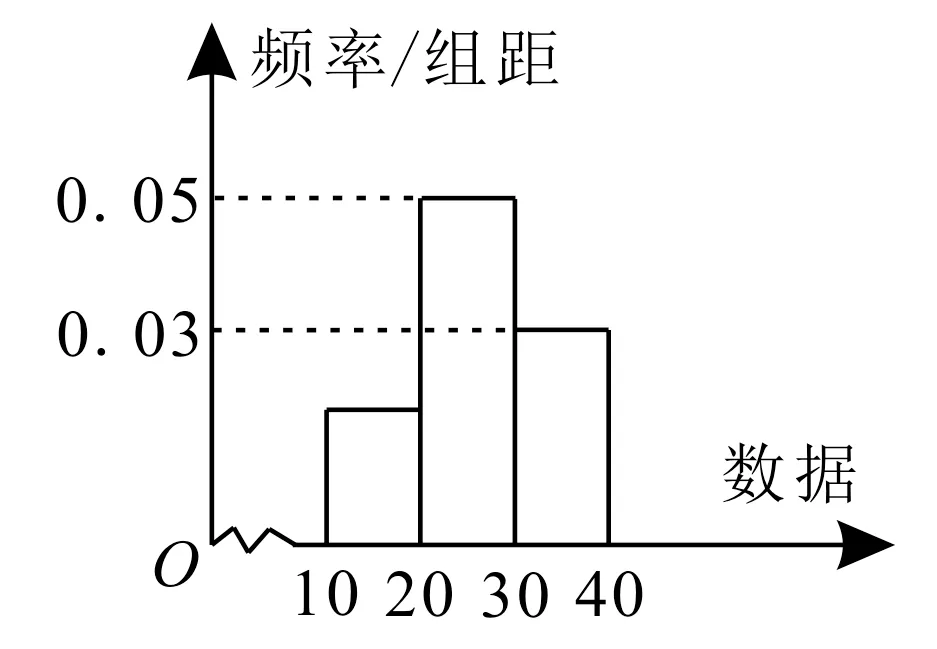
图5
A.0.02 B.0.2
C.0.08 D.0.8
解:由频率分布直方图可得,从左至右第一个小长方形的面积为1-(0.05×10+0.03×10)=0.2。应选B。
本题考查频率分布直方图中小长方形的面积的求法,考查频率分布直方图的性质,考查运算求解能力。在频率分布直方图中,小长方形的高长方形的面积,各小长方形的面积之和为1。

