数学习题编制策略

□ 杨劲芳

在数学教学中，练习和测验是必不可少的环节，对教学起着导向作用。如何让数学习题、试题编制更科学，以下策略供大家在编制试卷、习题时参考。

一、减少死记，关注知识技能的本源化

纯粹的计算题对部分学生来讲或许带有一定的机械模仿性，有时不妨换一个方式，考查一下学生是否真正理解计算过程中每一个数据的来龙去脉，变形式化的掌握为理解性的掌握。

【例1】

原题：列竖式计算21.6÷4。

现题：在右边的除法竖式中，方框内的16表示16个（）。

A.1 B.0.1 C.0.01 D.0.001

二、注重变式，提供知识应用的新情境

“基础”并不等同于“简单”，教师在命题过程中，可以给习题换个“马甲”，多创造一些适合知识运用的新情境。

【例2】

原题：A÷B=C（B≠0），则A=____。

现题：A÷B=C（B≠0，C≠0），则B×C÷A= _____。

原题和现题考查的知识点都是乘除法之间各部分的关系，现题给学生一个新的情境：两个相同的数相除（0除外），商为几？

【例3】

原题：某次语、数测验有21名学生至少一门功课达到了优秀，其中语文优秀的有16人，数学优秀的也有16人，语、数都优秀的有几人？

现题：将1、2、3、4、5、6六个数字填入图中的小圆圈内，使每个大圆圈上四个数字的和都是16。

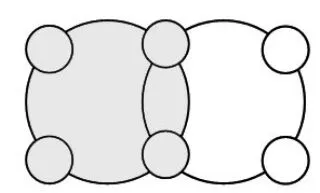
两道题都可用“16+16-（1+2+3+4+5+6）＝11”解决，在现题中，11是重叠部分的总和，中间重叠的圈内只能填5和6，所以边上两数之和是5，填1、4和2、3。现题在数阵图与韦恩图之间架起了桥梁，帮助学生领悟重叠问题的本质特征。

三、改变习题信息的呈现方式

试卷编制中，如果通篇都是用文字表达信息，会给人带来视觉疲劳。这时可适当改变信息的呈现方式，图文结合，也可考查学生的综合能力。

（一）图式方式呈现

【例4】

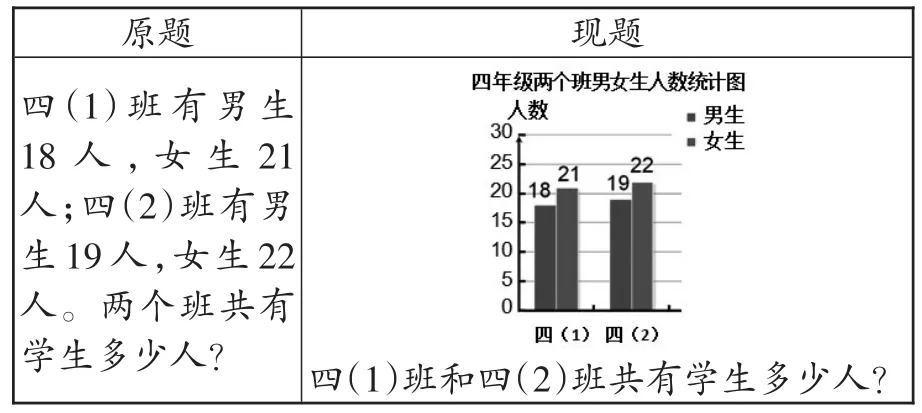
原题四（1）班有男生18人，女生 21人；四（2）班有男生19人，女生22人。两个班共有学生多少人？现题images/BZ_30_1723_1898_2011_2182.png四（1）班和四（2）班共有学生多少人？

将文字叙述题以统计图的形式呈现，培养学生读图提取信息的能力，也便于学生在计算总人数时，较为直观地交换加数位置而进行凑整：（18+22）+（21+19）。

【例5】

原题几次考试中，全班的平均成绩都是90分，男生的平均成绩是88分，女生的平均成绩是95分。已知男生有20人，求女生的人数。现题95分90分88分images/BZ_30_1909_2675_2113_2911.png

根据文字信息解答上题，学生理解起来比较困难，但如果将题目以“图形面积”形式呈现，易于学生理解和解答：男生共20人，由原平均成绩88分上升到现在的90分，则总共要增加（90-88）×20=40（分），而这40分是由女生来填补的；女生由原平均成绩95分下降到现在的90分，平均每人下降95-90=5（分），则女生有40÷5=8（人）。

【例6】

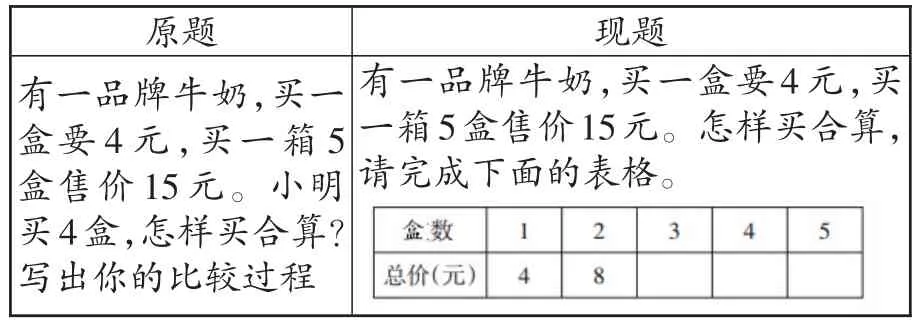
原题有一品牌牛奶，买一盒要4元，买一箱5盒售价15元。小明买4盒，怎样买合算？写出你的比较过程现题有一品牌牛奶，买一盒要4元，买一箱5盒售价15元。怎样买合算，请完成下面的表格。images/BZ_31_631_901_1150_1012.png

买3盒，则单买合算；但买4盒，单买需要16元，而买一箱5盒仅15元，更合算。这是对学生优化思维的一种挑战，这样的挑战也处在三年级学生的最近发展区。

（二）“图画—图形”方式呈现

由直接读取图中的数据方式转化为图形的数据读取方式，有助于提高学生对已知信息的获取和转换的能力。

【例7】

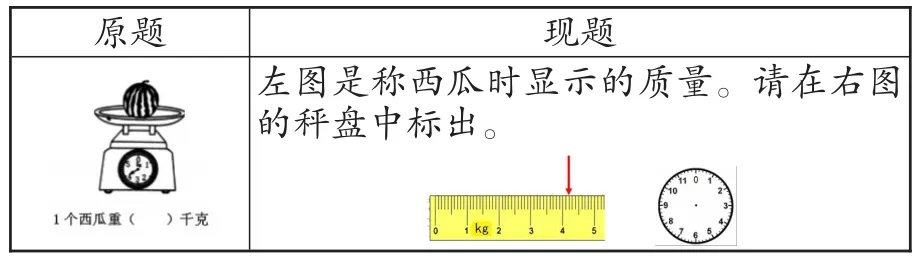
原题images/BZ_31_320_1754_487_1908.png现题左图是称西瓜时显示的质量。请在右图的秤盘中标出。images/BZ_31_696_1823_881_1922.pngimages/BZ_31_928_1844_1009_1922.png

（三）开放或半开放方式呈现

开放或半开放性的题，可以让学生不仅“知其然”，更能“知其所以然”。

【例8】

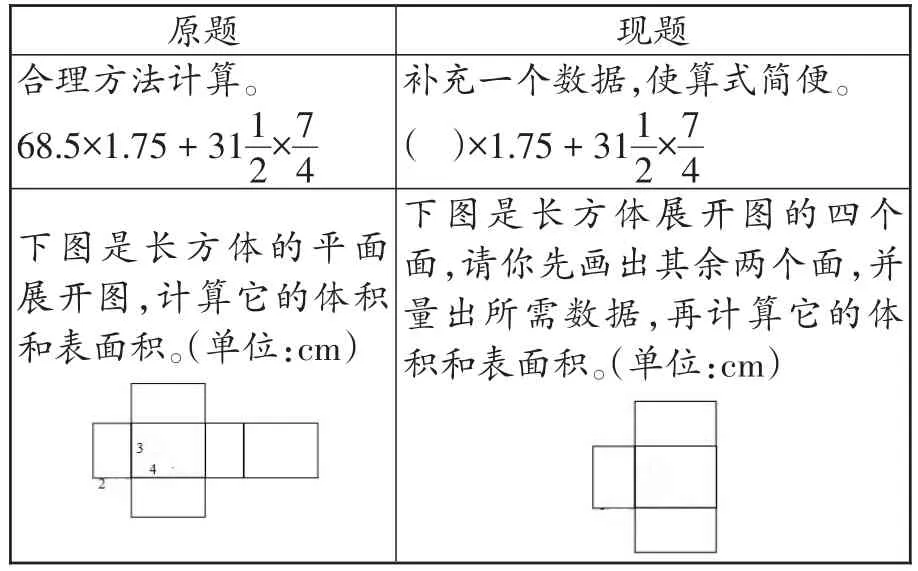
原题合理方法计算。68.5×1.75+311现题补充一个数据，使算式简便。（ ）×1.75+31 2×7 4 1 2×7 4下图是长方体的平面展开图，计算它的体积和表面积。（单位：cm）images/BZ_31_353_2613_600_2758.png下图是长方体展开图的四个面，请你先画出其余两个面，并量出所需数据，再计算它的体积和表面积。（单位：cm）images/BZ_31_855_2629_997_2792.png

四、注重习题解法的多样性

习题不仅要检测学生能否正确解答，更要检测学生能否理解和灵活应用数学知识。因此，让学生多角度去思考问题，寻求不同的解题方法，是教师命题所应追求的目标。

【例9】

此题的解答方法可以多样化，既能用比例解，也能用方程解，可满足不同思维方式的学生。

五、关注学科间知识的联系和整合

在命题中可以把多个科目、多个知识点结合在一起，考核的重点不再是知识点的简单记忆和重现，而是学生在分析解决实际问题中多方面的学习能力。

【例10】

如果下面的分数中，分子b表示水的量，分母a表示盐水的总量，那么对于盐水来说，如果“蒸发”掉一些水m后，它将变得更咸，这个结论可以用数学中的（ ）来解释。

【例11】

复式折线统计图关注的是两个量之间的比较，学生根据经验可以判断实线代表毛衣，虚线代表衬衫。

编制习题时，还可以把数学各领域的知识进行整合，既考查学生对知识的掌握情况，又检验学生综合运用知识的能力，可谓一举两得。

【例12】

如右图，点C、A、E在同一条线段上，线段DE与线段BC平行。问：三角形ABC和直角三角形ADE的面积之和是多少？（单位：分米）

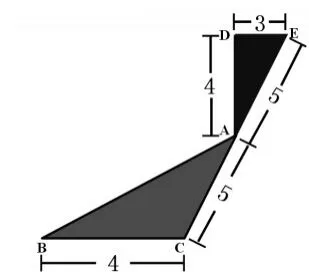
此题考查学生运用旋转及计算三角形面积的知识。