基于TI手持技术的高中数学实验教学策略探究
胡高嵩
摘 要 对TI手持技术在高中数学实验教学中的价值进行总结,并以高中数学“双曲线的几何性质”探究为例,从复习引入、形成概念、概念应用、小结归纳四个方面阐述TI手持技术在实践中的具体应用,最后深入反思,为TI手持技术在高中数学实验教学中的应用提供参考。
关键词 TI手持技术;高中数学;实验教学
中图分类号:G633.6 文献标识码:B
文章编号:1671-489X(2019)11-0115-03
1 前言
TI手持技术主要由TI图形计算器和无线导航系统组成,在一定程度上可以认为是现代计算器的高端产品。由于TI手持技术具有动态几何、数据收集、自动作图、代数运算、数据分析等功能,能够有效提升高中学生的数据运算和处理能力,提高动态演示运动轨迹、模拟实验等教学效率和质量;加之无线导航系统的应用,还可以组建专网专用的Ti-Nspire无线数学实验室系统,使数学资源传递更加及时,全面记录学生的学习信息。而在高中数学实验教学中,现代教学理念提倡借助计算机、计算器引导学生不斷进行探索和发现,但常用软件要么是只能做一些简单的计算,不利于学生开展数学实验探索,如Excel;要么是不擅长数据处理,如几何画板。并且受课时和教学环境的限制,其实验探究的效果并理想。因此,以TI手持技术为核心,通过“做数学”这种方式探究高中数学实验教学具有重要意义。
2 基于TI手持技术的高中数学实验教学的价值
有利于学生动手操作,促进学生主动思考 高中数学实验本身具有高度的抽象性,而由于传统技术条件的限制,学生常常是根据教师所呈现的结论机械记忆,一旦遇到变式题目或随着时间的推移,就难以正确解答。在高中数学实验教学中引入TI手持技术,教师可以根据所教内容,利用图形计算器合理设计内容,给学生认识提供直观感受,从而建立清晰的概念,帮助学生理解抽象知识。例如:
已知函数,当,请分别做出函数f(x)的图像。
该教学内容较为抽象,如果在教学中引入TI图形计算器,不仅会让学生产生强烈的求知和探索欲望,而且可以将抽象问题形象化、具体化,更容易让学生理解函数的性质。
有利于推理论证,提高学生的科学素养 高中数学教材提供了大量的素材,设计了大量的数学实验,很好地为学生探究搭建了一个学习平台。如果在数学实验中利用TI图形计算器主动钻研、验证假设,学生的学习不再受教师和教材的约束,有利于提升学生的数学学科素养。例如:
已知1只兔子每月生2只小兔,而两个月后每只小兔逐月生2只小兔。以此类推,如果年初仅有1只兔子,则一年后共有多少只兔子?
利用TI图形计算器,输入an=an-1+an-2,由于a1=1,a2=1,很容易求得a12=144,这种教学方法不仅让学生在兴趣盎然中获得了数列递推公式,而且也让学生在探索中获得了一种求知方法。
有利于激发学生学习兴趣,引导学生主动探究 高中数学给出许多问题,而这些问题都需要学生探个究竟。如果在高中数学实验中融入TI手持技术,可以很好地促使学生验证自己的想法,促进学生主动探究,并且有效避免烦琐的数学计算和枯燥的公式演算,从而将有限的时间和精力集中在数学实验活动的探索和分析上来。
如由于受思维定式的影响,相当数量的学生误认为cos(α+β)=cosα+cosβ成立,并不能从真正意义上理解,重视教师所讲的知识,而缺乏主动质疑并发展教师所讲内容的精神。运用TI手持技术,学生可以多次对α、β赋值进行验证,通过这样的学习方式加深印象,从而激发去寻求复角化单角的真实结论。同时,拓展知识维度,有效避免cos(α+β)=cosα+cosβ这样的错误结论。
3 基于TI手持技术的高中数学实验教学探究
基于TI手持技术的高中数学实验教学应立足于从教师 “教”转向为学生“学”,让学生逐渐从教学的参与者、协作者转变为教学的主体 圆锥曲线是高中数学的重点,也是学生学习的难点。虽然高中学生已经在必修部分学习过直线、圆等解析几何的相关内容,但未能真正将知识获得过程中所蕴含的推理、思维方法内化为自己的能力。圆锥曲线这一章节教学正可以发挥TI图形计算器的优势,因此,笔者以探究“双曲线的几何性质”为例进行深入探究。
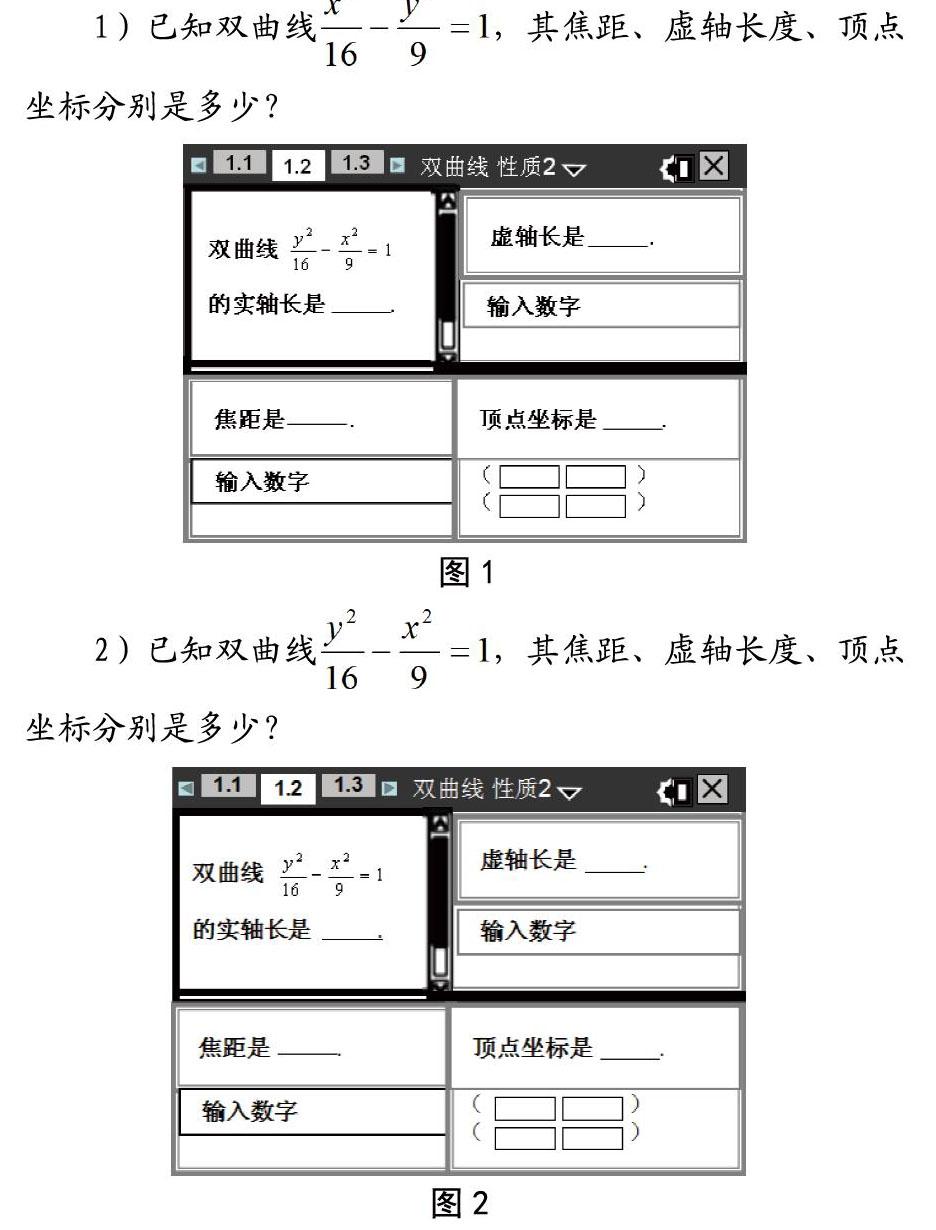
复习引入 为了复习旧知,将学生的思绪集中到双曲线几何性质的探究上来,教师及时利用TI无线系统的考试评价功能呈现图1、图2所示题目:
1)已知双曲线,其焦距、虚轴长度、顶点坐标分别是多少?
2)已知双曲线,其焦距、虚轴长度、顶点坐标分别是多少?
当学生做完相关题目后,教师运用TI教学软件直观统计学生解答结果,确保学生学情的及时反馈,并了解学生解题过程中出现的问题,当堂给予帮助和解决。
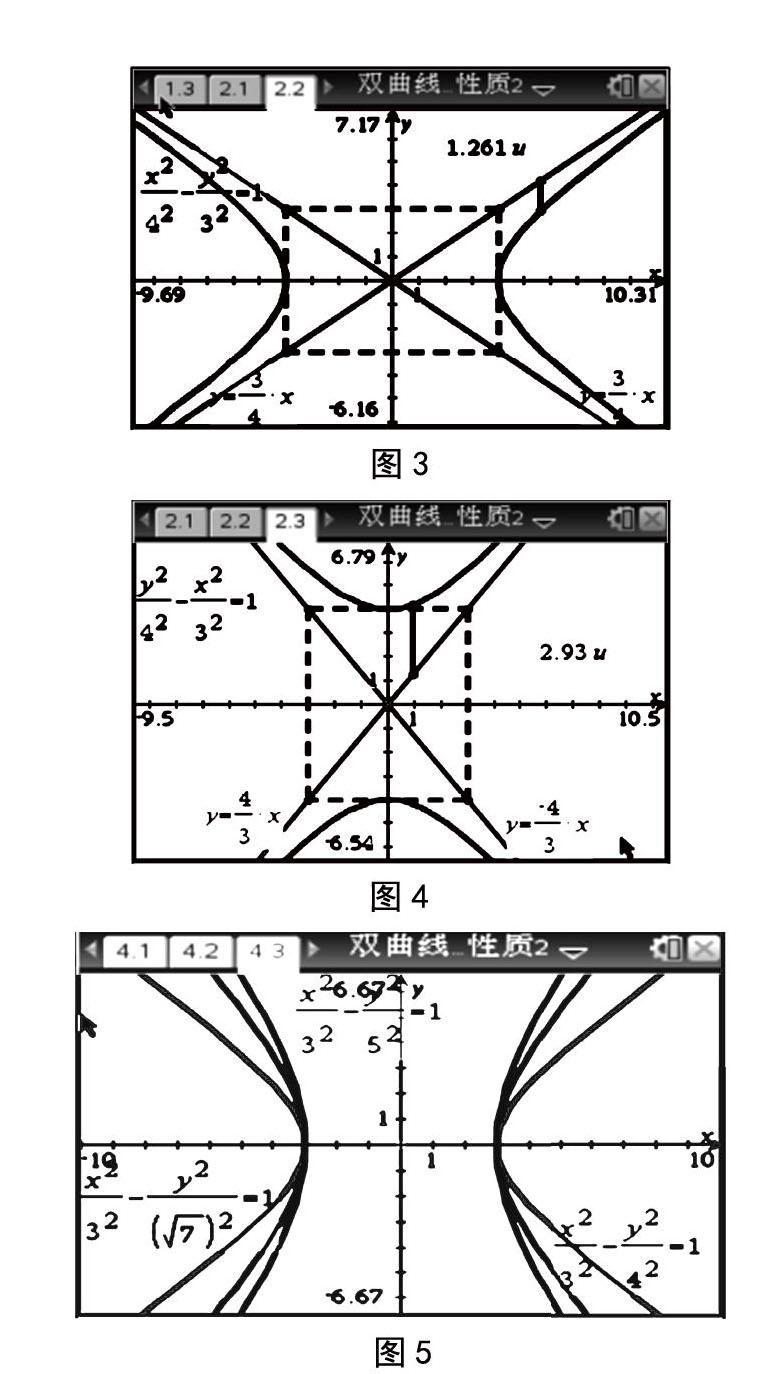
形成概念 为了探究出双曲线的渐近线存在性和方程,深刻理解渐近线无限接近的特征,要求学生利用TI图形计算器描绘出上述课前练习中和的图形,并画出以实轴、虚轴为边长的矩形,如图3、图4所示;然后利用TI图形计算器的图像功能,观察图3、图4中对角线与双曲线的关系,直观地感受对角线和对应双曲线之间无限接近的特征。
同时,为了探究出a、c值对双曲线形状的影响,离心率对双曲线形状的影响,要求学生在同一坐标系内画出四条不同的双曲线,如图5所示;然后观察图形,总结得出相关规律。值得注意的是,由于现行教材中已删除圆锥曲线的第二定律,教师可以利用TI图形计算器的图形功能有效地将抽象的知识转化为直观的图形,让学生在实际动手操作中感受a、c值对双曲线形状的影响。
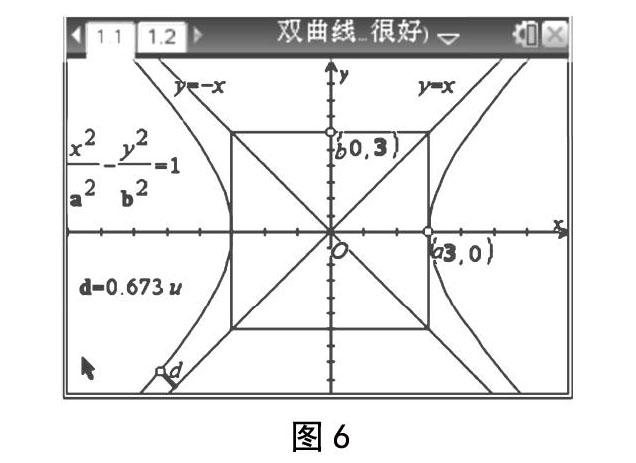
概念应用 在获得相关知识后,教师还应回归基础,运用渐近线和离心率综合解决以下问题。对于解题过程中有困难的学生,要求再次利用TI图形计算器和圆锥曲线的分析功能,如图6所示,在图形的直观认识后用“数”予以证明,或是由“数”的理论用图形加以验证,有效分析“数”与“形”之间的相互关系,从而树立学好数学的信心。
1)已知双曲线,其离心率为2,试求它的渐近线方程。
2)已知双曲线的一条渐近线方程为3x+4y=0,焦点坐标为(0,5),试求这条曲线的标准方程和离心率。
小结归纳 为了体现基于TI手持技术的高中数学实验教学评价的过程化、多元化,帮助学生认识自我,建立自信,了解学生发展中的需求,教师应首先组织学生自评,如我的猜想、探究、验证的能力如何?在此基础上组织学生进行小组互评,如小组发展的积极性和条理性如何?自己独立探究以及提出问题的能力如何?同时,以本节教学的收获或问题为主题,要求学生总结,不断完善自己的知识结构。
4 基于TI手持技術的高中数学实验教学反思
深入分析上述TI手持技术在“双曲线几何性质”教学中的实践,发现TI手持技术在高中数学实验教学中具有以下几个方面的优势,可为今后的教学实践提供参考。
从教师演示到学生操作,有利于调动学生的主观能动性 传统Excel、几何画板等图形绘制工具,虽然制作的图形精美、直观,但学生容易被精美的图形分散注意力,相当数量的学生将精力集中在如何利用计算机制作出精美的图形,这并不代表学生参与课堂教学,无法达到让学生深入思考教师展示图形的真正目的,导致学生出现过目就忘的现象。TI手持技术的应用使得课堂教学中学生的手、眼、脑全部参与,正如教育家苏霍姆林斯基所说:“儿童的智慧在他们的指尖上。”
师生互动,更加准确地把握学生的学习状态 TI手持技术在高中数学教学中的应用,可以使得教师将预先设定的题目通过无线接收装置发送到学生的计算器上,学生作答后第一时间反馈统计,有利于教师随时了解每位学生对知识的掌握情况,并在教学活动中根据学生实际学习情况调整教学安排,做到有的放矢。同时,在实验自主探究中,教师可以将每位学生计算器的界面呈现到电脑上,有助于学生与学生之间相互借鉴,展示探究结果;并且可以从动态窗口中看到每个学生的操作过程和进度,方便关注学生是否积极有效地探究问题,便于给予学生帮助和指导。
促进学习方式、教学方式的转变 由于传统教学方式的影响,相当数量的学生只关注题目的解题结果,机械地记忆题型和公式,而忽略了学习思维和探究能力的培养。使用TI手持技术时,教师更加强调的是学生的操作、实验、探究等一系列活动,注重的是学生发现问题、发展学习的能力,有利于学生与学生之间形成一种自主合作的学习方式,正如数学教育家弗赖登塔尔所说:“数学知识是研究出来的,不是教和学出来的。”同时,教师从学习的倡导者变为学习的组织者,有效为师生营造了共同需要的氛围。
5 结语
总之,基于TI手持技术的高中数学实验教学注重学生的思维发展,注重知识的形成过程,是现代教学理念的充分体现和有益尝试。因此,在具体教学实践中,教师应转变角色,因势利导,积极组织学生动手、动脑,利用TI手持技术“做数学”。只有这样,才能培养学生的探究能力,才能促使学生应用数学思想和数学方法观察、认识世界,才能发现和发展学生多方面的潜能。
参考文献
[1]崔友红.两例概率统计案例的TI手持技术求解[J].中学数学研究:华南师范大学版,2014(5):20-21.
[2]黄炳锋,金克勤.TI手持技术在高中数学教学中的运用方式研究:以“函数图象变换”的教学为例[J].数学通报,2015(4):19-23.
[3]施峥.TI图形计算器在高中数学教学中的应用:以幂函数教学为例[J].数学学习与研究:教研版,2017(13):103,105.

