ZW12断块E2s16砂组老井水淹快速评价初探
黄 帅,梅海燕
(1.西南石油大学石油与天然气工程学院,四川成都 610500;2.中国石化江苏油田分公司物资供应处,江苏扬州225009)
油田开发中后期由于经过长期注水,油藏内的流体甚至岩石骨架等均发生了明显变化,对油藏的水淹状况和流场均产生了不可忽视的影响[1-4]。并且油田水淹程度和水淹层解释是老油田稳产的重要研究内容,老油田往往老井多,测井资料等数据仍停留在油藏开发初期的状态,后期大量重新补充测井费用巨大,因而如何利用老井资料开展水淹层评价研究给油气开发科研工作带来了挑战[5-8]。
通过对老油田的具体特征分析,油田开发中后期具有完善的井网、井距条件及丰富的加密、调整、侧钻、更新、检查井资料,并具有十几年甚至几十年的生产数据。通过对老油田测井及生产资料的分析,提出了以老井含水率和电阻率为基础的一种老井水淹状况快速评价方法。
1 老井水淹状况评价方法
测井技术是油田开发中后期油藏精细描述中评价储层及流体饱和度变化情况等研究的主要技术之一,起着其他方法无法替代的作用。同时,现阶段采用的测井解释理论及经验公式基本上已经固定下来,例如含油饱和度计算采用的阿尔奇公式等[9]。此外,前人在利用生产测井资料确定剩余油饱和度方面也做了相关研究[10-11],提出了相应的解释方法。但是在油田具体生产中,存在生产测井资料的井较少,采用现有的理论难于解决老井在原有测井数据情况下如何快速解释水淹特征的问题。
从理论上分析,影响剩余油饱和度的主要测井参数是电阻率[12-13],而生产资料中的含水率是目前最能真实反映油田地下流体动态的信息,因而考虑通过建立目的层段的含水率和电阻率之间的关系来实现水淹层定量评价的目的。
在实际资料处理过程中发现,对于同一类型的沉积微相解释层而言,钻遇不同砂体的原始电阻率值R0不同[14],因而利用电阻率比值的方法,采用合适的数学方法与含水率模拟,建立“含水率/电阻率”数学模型。
图1中A、B、C、D代表不同沉积类型砂体。针对同一类型沉积砂体,第一口钻遇此砂体的电阻率记为R0(油藏原始电阻率),其他时期钻遇的井,其单井初始电阻率和初始含水率记为Rt和Fw,则按钻遇时间排序为:A1(Rt1,Fw1)、A2(Rt2,Fw2)、…、Ai(Rti,Fwi)、…、An(Rtn,Fwn)。
为消除原始电阻率影响,则:



图1 高含水油藏老井水淹状况解释方法地质模式Fig.1 Geological model of interpretation for old wells in high water cut reservoir under water flooded condition
式(3)可以解决已知老井目前含水率Fwi,校正老井电阻率Rti,通过阿尔奇公式可以计算老井现在的剩余油饱和度,从而对老井的水淹状况进行判别。
2 地区评价应用
2.1 水淹状况评价公式推导
本次研究选择具有三十多年开发历史的ZW油田开展研究,ZW油田ZW12断块E2s16砂组为辫状河道砂体,选取钻遇此砂体不同时期的9口井,通过油藏开发初期电阻率统计油藏原始电阻率R0取值29.30 Ω·m,统计各口井的初始电阻率(Rt)、初始含水率(Fw)和目前含水率(Fwi)等参数(表1)。
根据以上数据,建立电阻率比值与原始含水率的关系(图2)。
得出辫状河道砂体:

由公式(4)转化得:
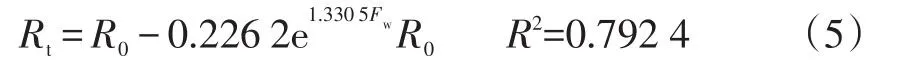
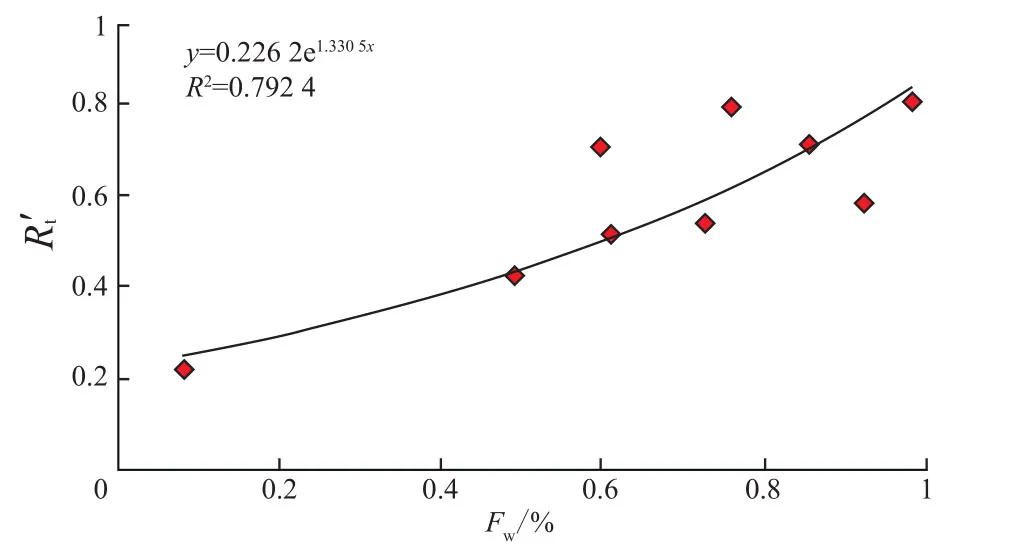
图2 ZW油田辫状河道砂体电阻率比值与原始含水率关系Fig.2 Intersection diagram of resistivity ratio and original water content of sand body in braided channel of ZW Oilfield
即

根据式(5)及式(6),通过对老井含水率Fw的统计,可以反推老井目前的电阻率,从而计算老井的剩余油饱和度。同理,也可以建立曲流河(ZW油田E2s14+E2s15)、三角洲(ZW油田E2s17)、扇三角洲相(ZW油田E2d22)的主力含油砂体相应研究公式。
2.2 老井电阻率校正
已知目前含水率,通过建立的油藏原始电阻率(R0)、单井初始电阻率(Rt)和原始含水率(Fw)的拟合公式,可以进行电阻率的计算,从而校正老井电阻率。以ZW12断块辫状河道的9口井为例,利用式(7)进行老井电阻率校正,计算结果见表1。

从表1中可以看出,目前地下储层电阻率都有不同程度的降低,其减小幅度与油井目前的含水率和油藏开发时间有关,含水率越高,电阻率减小程度越大,反之亦然;钻井时间越早,初始电阻率就越高,电阻率减小程度也就越大。如ZW116井目前含水率为0.709,其电阻率减小了1.9 Ω·m;而ZW124井目前含水率已达0.941,其电阻率目前仅有6.14 Ω·m,比原始电阻率减小了7.4 Ω·m。
该方法当没有老井目前含水率资料时,如果存在生产测井资料,可以通过生产测井资料中的持水率(Yw)来计算含水率,进而计算剩余油饱和度[11-13]。当生产测井资料也缺少时,弥补方法是用邻近钻遇同一沉积砂体井的含水率代替该井含水率,进而求取该电阻率值,实现老井电阻率校正,但该弥补方法在实际操作过程中存在较大误差,不建议使用。
2.3 水淹解释结果及方法检验
ZW油田储层属于孔隙型砂岩储层,可以采用阿尔奇公式计算研究区的含油饱和度[15-17]。其解释模型为:

式中:Sw为含水饱和度,%;Rw为地层水电阻率,Ω·m;Rt为感应电阻率,Ω·m;m、a为岩石胶结指数;n、b为饱和度指数;φ为储层有效孔隙度,%;So为含油饱和度,%。

图3 ZJ1井测井解释结果Fig.3 Logging interpretation result of well-ZJ1

表1 研究区辫状河道相砂体各井参数统计Table1 Statistics of parameters of sand body in braided channel of work area

表2 ZJ4井测井解释与岩心分析对比Table2 Comparison between logging interpretation and core analysis of well-ZJ4
在实现了老井电阻率校正计算后,通过阿尔奇公式获得老井目前的剩余油饱和度,从而可以按照研究区水淹标准快速判断该井的水淹情况[11-13]。通过对密闭取心井ZJ1井的测井解释结果(图3)与原始解释对比可以看出,目前解释结果与原始解释结果基本一致,仅有1 943.8~1 951.9 m处解释存在差别。该层由于上部剩余油饱和度较高,导致该小层平均含油饱和度解释结果较高。从生产情况分析,该层投产后含水率较低,初期含水率仅为32%左右,因而认为该层解释为油层更为合理。并且该方法的解释结果也可以为研究区数模结果的验证提供依据。
为进一步验证该方法的准确性,选择ZW油田2015年钻探的一口密闭取心井ZJ4井,使用含水率法对该井取心层段的含油饱和度So进行计算,进而判断目的层段的水淹情况(表2)。通过对多个小层的计算,可以看出解释结果基本一致。但部分层位的含油饱和度绝对误差较大(大于5%),水淹程度的判别与实验结果也一致,所以“含水率/电阻率”法老井水淹状况快速解释方法在快速定性—半定量判别水淹状况方面具有较高的实用性,在定量方面需要进一步的细化储层分类,以提高其准确性。
3 结论
1)通过各井初始电阻率和初始含水率建立了同一沉积类型砂体的含水率和电阻率关系经验公式,并利用阿尔奇公式计算老井现在的剩余油饱和度,提出了以老井含水率和电阻率为基础的一种高含水油藏老井水淹状况快速评价方法。
2)建立了ZW12断块E2s16砂组辫状河道砂体电阻率比值与原始含水率的关系公式,进一步计算了该区各个小层的校正电阻率,并通过密闭取心井ZJ1井和ZJ4井取心段含油饱和度的计算,对该方法的准确性进行了验证。

