封闭断层复合油藏压裂井压力动态特征

姬安召，王玉风

（陇东学院能源工程学院，甘肃庆阳745100）

对复合油藏而言，断层的存在影响单井产量，同时断层的位置也影响井底压力的变化[1]。在复合油藏试井解释模型研究方面，国外学者LOUCKS等[2]和EGGENCHWILER等[3]建立了直井径向复合油藏试井解释模型并分析了井底压力曲线的变化特征。在GRINGARTEN、RAMEY等[4]研究实空间点源函数解的基础上，OZKAN等[5]将实空间点源解扩展到Laplace空间并给出了详细的计算方法。在复合油藏压裂井井底压力动态特征研究方面，国外学者CHU、CHEN等[6-7]基于点源函数基本理论，建立了复合油藏均匀流量裂缝井试井数学模型，结合CINCO-LEY等[8]对有限垂直导流裂缝的研究成果，得到有限导流复合油藏压裂井试井解释模型，并对Bessel函数Kn(x)和In(x)的计算进行了讨论。在国内，陈军、何应付、蔡明金、赵玉龙等[9-12]基于点源函数基本理论，对复合油藏有限导流压裂井试井解释模型做了进一步研究，绘制了井底压力典型特征曲线并进行影响因素分析。冯纪成、曾杨和张望明等[13-15]对储层中含有直线断层的压裂井试井解释模型进行了深入研究，分析了断层对试井曲线的影响。刘启国等[16]对复合油藏存在直线断层直井井底压力动态进行了研究，并分析了镜像井位于内区和外区时井底压力响应特征。

目前关于考虑断层径向复合油藏压裂井试井解释模型研究较少，已有的研究成果大部分是基于均质油藏存在直线断层压裂井的井底压力动态特征，或是径向复合油藏含有直线断层直井的压力动态特征方面的研究。因此，根据点源函数基本理论，建立径向复合油藏压裂井均匀流量试井解释模型，考虑储层与流体之间的耦合关系，求解得到径向复合油藏有限导流压裂井井底压力解，利用镜像反映原理和Stehfest[17]数值反演方法，得到考虑断层情况下实空间井底压力数值解，分析断层位置以及其他影响因素对井底压力与压力导数曲线的影响，为含有断层的径向复合油藏压裂井的试井解释提供理论指导。

1 双区复合压裂井模型建立与求解

1.1 物理模型描述

由于泥浆的侵入或流体的注入使得井底附近与远离井筒附近流体物性和岩石物性有一定的差别，此外，由于油水边缘的收缩也会导致两个不同流动区域的形成。因此，复合油藏模型具有普遍的实际意义。径向复合油藏压裂井模型见图1，其基本假设条件如下：

1）井位于两区径向复合油藏的中心，地层水平等厚，两个区域流体物性和岩石参数不同，内区半径为rm。

2）地层中流体为单相、弱可压缩的液体，忽略重力和毛管力的影响。

3）各区流体流动均符合达西渗流规律，并且流体在油藏的渗流为等温渗流。

4）裂缝半长为Lf，裂缝宽度为Wf。

图1 复合油压裂井物理模型Fig.1 Physical model of fractured well for composite reservoir

5）不考虑井筒储集和表皮效应的影响。

1.2 复合油藏压裂井模型建立与求解

根据Ozkan[5]的研究，Laplace空间点源解可用式（1）表示：

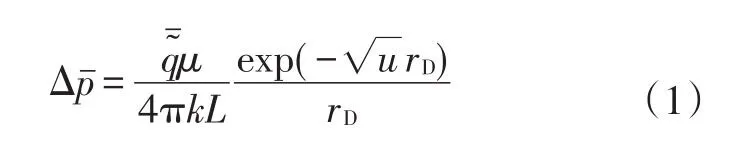
式中：Δˉ为Laplace空间压差，Paˉ为Laplace空间瞬时流量，m3/s；μ为流体黏度，Pa·s；k为储层渗透率，10-3μm2；L为参考长度，取裂缝的半长，m；rD为无因次距离；u为Laplace变量。

根据式（1）所给的Laplace空间点源解，利用镜像原理、压降叠加原理，求出上下边界封闭，水平方向无限大时点源函数基本解为：

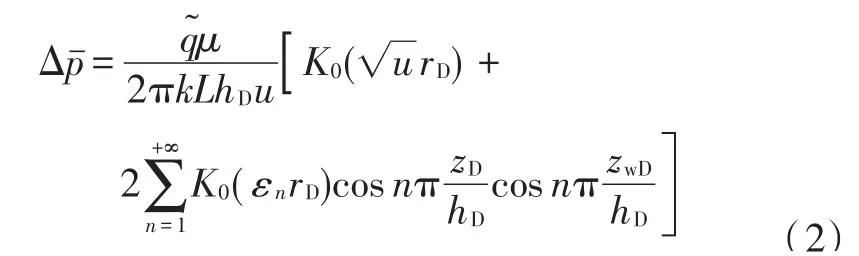
为了方便求解双区径向复合油藏压裂井的试井解释模型，需要定义如下无因次变量：

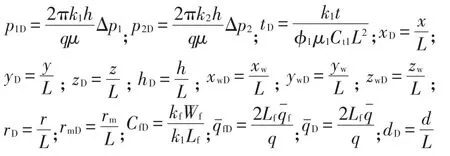
其中：p1D，p2D分别为内区与外区无因次压力；k1，k2分别为内区与外区储层渗透率，m2；q井在地下产量，m3/s；Δp1，Δp2分别为内区与外区的压差，Pa；tD为无因次生产时间；t为生产时间，s；φ1为内区储层孔隙度；μ1为内区储层流体黏度，Pa·s；Ct1为内区储层综合压缩系数，1/Pa；xD，yD分别为储层中任意点在x与y轴方向的无因次坐标值；x，y，z分别为储层中任意点在直角坐标系中的坐标值，m；h为储层有效厚度，m；xwD，ywD分别为井在x与y方向无因次坐标值；xw，yw，zw分别为井在直角坐标系中的坐标值，m；r为储层中任意点在柱坐标系中径向方向的距离，m；rm为内区半径，m；rmD为内区无因次半径，m；CfD为裂缝无因次导流系数；kf为裂缝渗透率，m2；Lf为裂缝长度的一半，m；Wf为裂缝宽度，m；fD为Laplace空间裂缝无因次流量；f为Laplace空间单位长度裂缝的流量，m2/s；D为Laplace空间油井的无因次产量；为Laplace空间单位长度裂缝的产量，m2/s；dD为压裂井到断层无因次距离；d为压裂井到断层的距离，m。

对于径向复合油藏而言，根据运动方程、状态方程和连续性微分方程，分别建立内区与外区渗流数学模型，同时考虑内边界井底定产、径向方向外区外边界无限大、上下地层界面封闭、内区与外区分界面处流量相等条件。对渗流数学模型、边界条件及初始条件进行无因次化，然后经过Laplace变换之后得到的渗流微分方程为：

对式（3），首先根据OZKAN的研究结果[5]，内区渗流微分方程的解可由两部分构成，一部分关于上下边界的解，另一部分关于圆形外边界的解，对于点源来讲，同样符合上述条件。对于渗流微分方程而言，内边界定产，外边界径向方向无限大，顶底边界封闭，因此，可采用式（2）的形式表示出外区渗流微分方程的通解。在式（3）求解的过程中再利用式（4）关系：

式中：Iv(x)，Kv(x)分别为v阶第一类、第二类 Bessel函数；Iv'(x)，Kv'(x)分别为v阶第一类、第二类Bessel函数的导数；z1为v阶第一类、第二类Bessel函数自变量。

求解式（3）得到储层内区与外区压力解为：

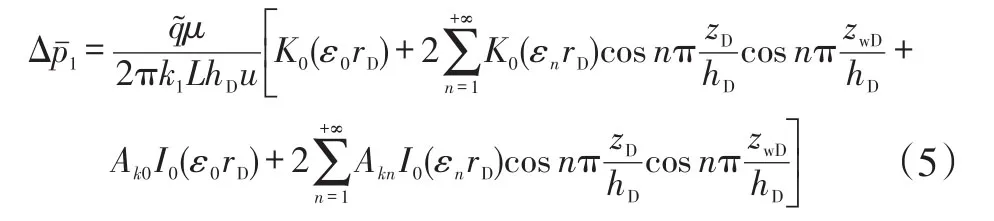
对于式（5）而言，中括号中与K0(x)相关的部分表示顶底封闭边界、径向无限大油藏压力解，与I0(x)相关的部分表示顶底封闭边界、径向复合、圆形封闭和圆形定压边界油藏压力解，在研究模型中特指径向复合油藏无限大径向外边界压力解。

式（5）—式（6）中：

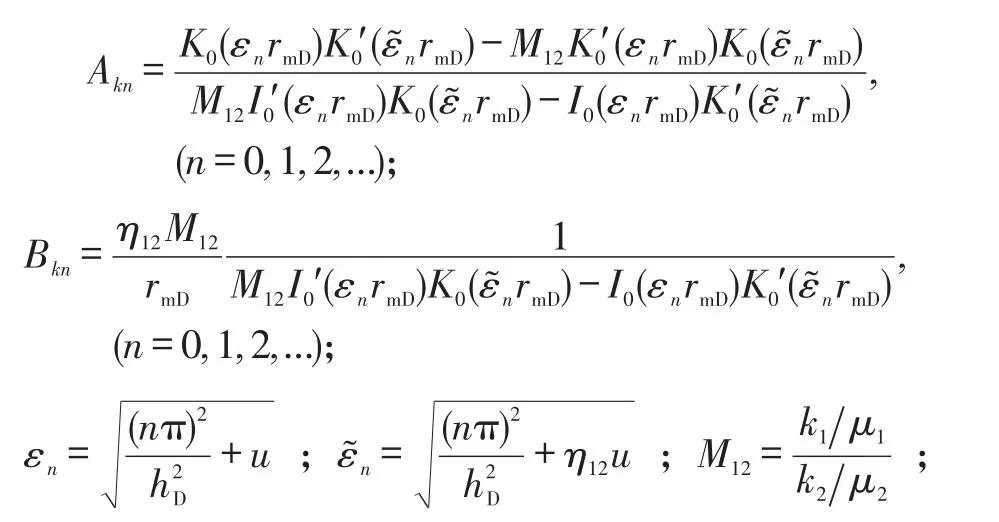
对式（5）和式（6），分别沿z方向从0到h，再沿x方向从-Lf到Lf积分得到径向复合油藏完全射开垂直裂缝井井底压力、储层内区与外区压力，其无因次压力形式为：

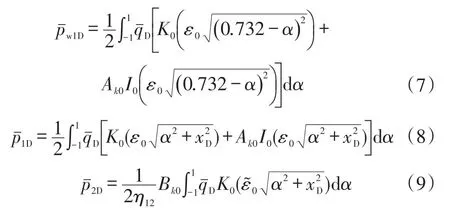
式（7）—式（9）中：为Laplace空间无限垂直导流裂缝的无因次井底压力；，分别为储层内区与外区Laplace空间无因次压力；α为积分变量。

关于有限导流裂缝函数的计算，CINCO-LEY等[8]将裂缝模型与储层模型耦合求解得到有限导流垂直裂缝井的井底压力解，裂缝与储层模型耦合解可以写为以下形式：

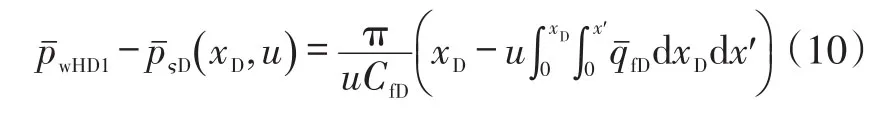
式中：为Laplace空间有限导流垂直裂缝无因次井底压力；D为Laplace空间无限导流垂直裂缝的无因次压力，下标ς分别为w1，1，2；x'为积分变量。

在式（10）中，要计算有限导流裂缝的井底压力，首先要知道裂缝流量，对于定产量生产的油井而言，流量关系如下：

在裂缝壁面处，虽然整个裂缝长度内流量不相等，但沿着裂缝很小一段距离内，可以假设流量恒定，因此，对式（10）、式（11）进行离散可以得到复合油藏压裂井井底压力解为：

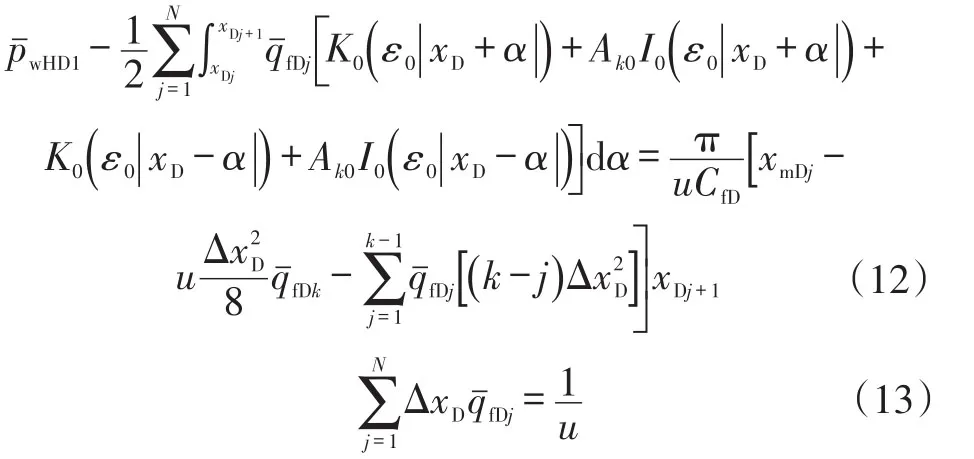
1.3 考虑封闭直线断层复合油藏压裂井模型解

对于考虑封闭断层的径向复合油藏而言，断层的位置影响井底压力和井底压力导数曲线的变化形态，因此分两种情况对其进行讨论：镜像井在内区（图2a）和镜像井在外区（图2b）。

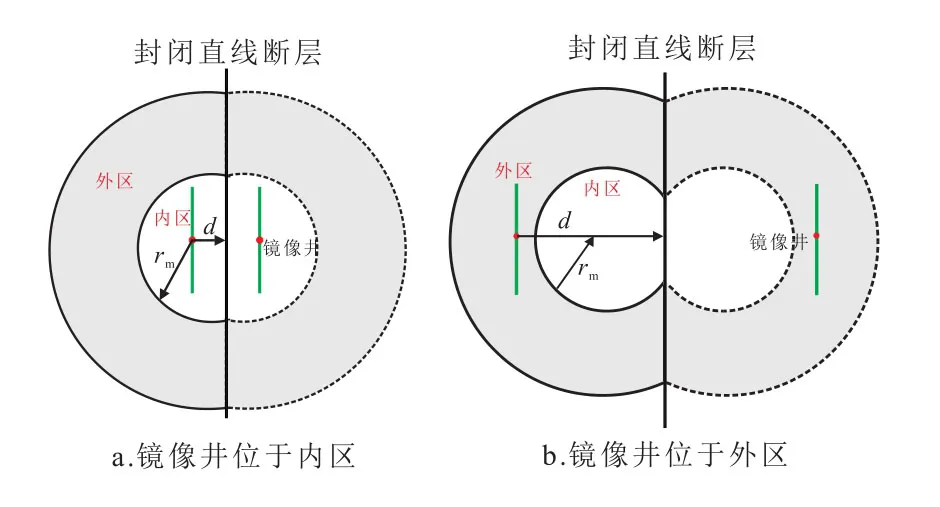
图2 复合油藏考虑封闭断层物理模型Fig.2 Physical model of composite reservoir with closed fault

针对上述两种不同的情况，根据镜像反映法和叠加原理，分别得到不考虑井储和表皮时的井底压力。

1）镜像井位于内区

假定压裂井到封闭直线断层的距离为d，单位m，当d＜rm/2且镜像压裂井不穿过内区边界时，镜像井位于复合油藏内区，压裂井井底压力响应函数可以表示为：

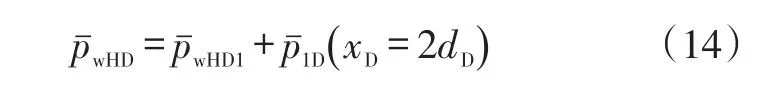
式中：wHD为考虑封闭断层的Laplace空间无因次井底压力；dD为压裂井到封闭直线断层的无因次距离。

2）镜像井位于外区

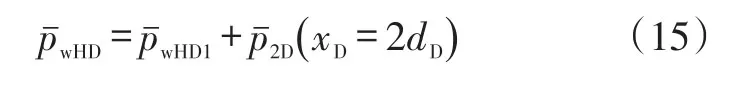
假定压裂井到封闭直线断层的距离为d，单位m，当d＞rm/2且镜像压裂井不穿过内区边界时，镜像井位于复合油藏外区，压裂井井底压力响应函数可以表示为：入式（8）和式（9）进行积分，可以得出镜像井位于内区与外区时形成的压力降，然后通过式（14）和式（15）的叠加原理就可以得到考虑封闭断层复合油藏有限导流垂直裂缝井井底压力解。

考虑井储和表皮影响时，根据杜哈美原理可得井底压力解：

式中：wD为考虑井储与表皮系数的Laplace空间无因次井底压力；CD为无量纲井筒储集系数；S为表皮系数。

2 曲线特征与影响因素分析

通过计算机编程求解式（14）—（16），分别得到镜像井位于内区与外区时的井底无因次压力。图3为镜像井位于内区井底无因次压力响应特征曲线。考虑封闭断层存在时，取内区无因次半径rmD=2 000，内区与外区流度比M12=4，井底无因次井底压力与压力导数曲线总体上划分为7个流动阶段。第一阶段为早期井储和表皮反映阶段，纯井储阶段井底无因次压力与压力导数曲线重合并呈斜率为1的直线，井储和表皮共同作用时井底无因次压力导数曲线呈明显驼峰；第二阶段为双线性流阶段，该阶段为裂缝和储层流体的线性流同时发生，在理想情况下，井底无因次压力和压力导数曲线平行且呈斜率为0.25的直线；第三阶段为储层流体的线性流阶段，该阶段为储层流体向裂缝流动，井底无因次压力导数曲线呈斜率为0.5的直线；第四阶段为椭圆流阶段，该阶段为储层流体围绕裂缝的椭圆流，井底无因次压力导数曲线呈斜率为0.36的直线；第五阶段为内区径向流阶段，该阶段井底无因次压力导数曲线呈值为0.5的水平线；第六阶段为直线封闭断层反映阶段，该阶段井底压力导数曲线呈值为1的水平线，在内区半径一定的情况下，断层到压裂井的距离越近，断层反映阶段越明显，内区径向流持续时间越短；第七阶段为外区径向阶段，考虑直线封闭断层时，该阶段井底压力导数曲线呈值为M12的水平线，不考虑封闭断层时，该阶段井底压力导数曲线呈值为0.5M12的水平线。文中取流度比为4，做出了井底无因次压力与压力导数的特征曲线。在实际试井分析过程中，可根据现场的实际情况进行取值。流度比对井底无因次压力曲线与压力导数曲线都有影响，但对井底无因次压力导数曲线影响更明显，主要反映断层响应段与外区径向流阶段井底无因次压力导数曲线水平段的位置，如图3所示。

图3 镜像井位于内区时井底压力响应特征曲线Fig.3 Characteristic curve of pressure response when the mirror well is located in the inner part

图4为镜像井位于外区井底压力响应特征曲线。考虑封闭断层存在时，取内区无因次半径rmD=2 000，内区与外区流度比M12=4，该特征曲线总体上分为七个流动阶段，压力波没有传播到内区边界时，其曲线特征与图3相同，当压力波传播到外区时，第六阶段井底压力导数曲线呈值为0.5M12水平线，断层距离井中心越远，外区径向流持续时间越长。第七阶段为直线封闭断层反映阶段，该阶段井底无因次压力导数曲线呈值为M12的水平线。

图5为裂缝导流能力对特征曲线的影响。裂缝无因次导流系数CfD表征裂缝导流能力的大小，裂缝无因次导流系数越大，裂缝导流能力越强，流体流入井底所消耗的压力损失就越小。内区无因次半径与流度比的取值与图3一致，从典型特征曲线图5可以看出，裂缝无因次导流系数越大，双线性流阶段结束的时间越早，早期井底无因次压力和压力导数曲线值越小。

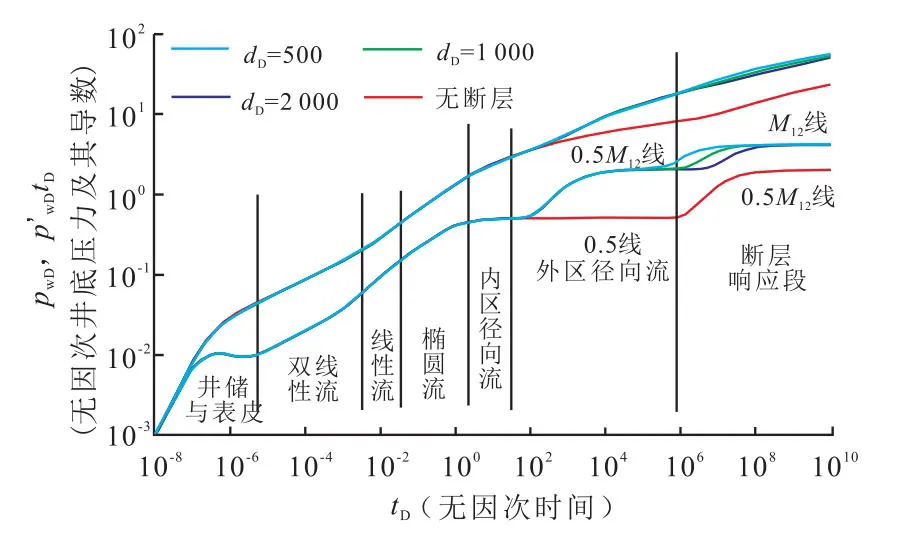
图4 镜像井位于外区井底压力响应特征曲线Fig.4 Characteristic curve of pressure response when the mirror well is located in the outer part

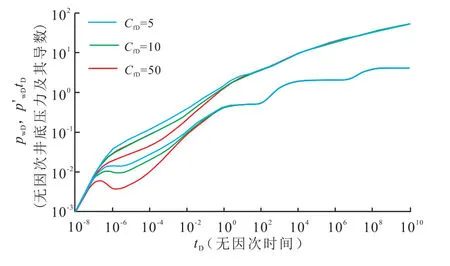
图5 裂缝导流能力对特征曲线的影响Fig.5 Influence of fracture conductivity on typical curves

图6为内区半径对特征曲线的影响。当镜像井位于内区时，压力波向外传播首先遇到断层，在井底无因次压力导数曲线呈值为1的水平线，压力波继续向外传播，当压力波传播到内区边界时，由于内外区流体性质不同，所以井底压力导数曲线呈值为M12的水平线，内区半径越小，压力波传播到外区所需要的时间越短，井底无因次压力导数曲线M12水平线开始的时间越早（图6a）。当镜像井位于外区时，压力波向外传播首先遇到内边界，由于内外区流体性质不同，内区径向流之后井底无因次压力导数曲线呈值为0.5M12的水平线，内区半径越小，压力波传播到外区所需要的时间越短，井底无因次压力导数曲线呈值为0.5M12水平线开始的时间越早，当压力波传播到封闭断层时，井底无因次压力导数曲线呈值为0.5M12水平线上升到M12水平线（图6b）。

图6 内区半径对特征曲线的影响Fig.6 Influence of inner radius on typical curves

3 结论

1）复合油藏压裂井考虑封闭断层时，镜像井的位置对井底压力导数曲线形态具有一定影响，在径向流阶段之前井底无因次压力与压力导数曲线重合。

2）镜像井位于内区时，主要的渗流阶段依次为内区径向流阶段、断层反映阶段和外区径向流阶段，其井底无因次压力导数曲线分别呈值为0.5、1和M12的水平直线。

3）镜像井位于外区时，主要的渗流阶段依次为内区径向流阶段、外区径向流阶段和断层反映阶段，其井底无因次压力导数曲线分别呈值为0.5、0.5M12和M12的水平直线。

4）裂缝导流能力只影响双线性流和线性流阶段井底无因次压力和压力导数曲线形态，裂缝无因次导流系数越大，双线性流和线性流阶段井底无因次压力和压力导数曲线幅度越低。