稳态法测量导热系数面积修正误差分析

程德胜，张 辉，马书炳，王申浩, 鲍莉娜

(陆军炮兵防空兵学院 物理教研室,安徽 合肥 230031)

导热系数是表征物质热传导性质的物理量. 材料结构的变化与所含杂质的不同对材料导热系数都有明显的影响，因此材料的导热系数常需实验具体测定. 测量导热系数的实验方法一般分为稳态法与动态法. 在稳态法中，利用热源对样品加热，适当控制实验条件和实验参量使加热和传热过程达到平衡状态，通过测量同等条件下散热盘的散热率并进行面积修正计算出物体的导热系数，而面积修正系数的取舍对导热系数的测量有很大影响，本文从数值模拟的角度分析面积修正系数对导热系数测量的影响，为实验教学提供参考依据.

1 稳态法测量不良导体导热系数原理

1.1 傅里叶热传导方程

傅里叶热传导方程正确地反映了材料内部的热传导的基本规律. 该方程式指出：在物体内部，垂直于热传导方向彼此相距h，温度分别是T1和T2(T1>T2)的2个平行平面之间，当平面的面积为S时，单位时间δt内通过该面积的热量δQ为

(1)

式(1)中δQ/δt为热流量与传热面积S、温度差T1-T2成正比，与距离h成反比，其比例系数即为导热系数λ，它只与材料性质有关，其单位是W/(m-1·K-1).

1.2 实验中用稳态平板法测不良导体的导热系数的原理

实验装置的原理如图1所示,发热盘A连接电炉提供加热热流，散热盘P对外自由散热，散热盘P和发热盘A之间夹着圆形待测样品B，其上、下表面温度分别由安插在A和P盘侧面深孔中的温度传感器测量.

图1 稳态法测量导热系数实验原理示意图

由式(1)可知，当样品的厚度足够薄，样品侧面散热量相对截面的热传导可忽略不计，单位时间内通过待测试样B的任一圆截面的热流量为

(2)

式中：hB为样品厚度，rB为圆盘样品的半径. 当传热达到稳定状态时(稳态)，T1和T2值不变，此时样品内有稳定的温度梯度，对于样品内的任一圆截面及铜盘A和P来说，单位时间内流入的热量等于流出的热量. 对铜盘P，单位时间内流出的热量即为向周围环境散热的速率，单位时间内流入的热量即为热流量δQ/δt. 因此可通过P盘在稳定温度T2时的散热速率求热流量.

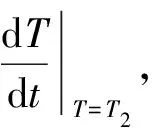
(3)

式(3)中a为温度为T2的铜盘P在环境温度为T0条件下的表面换热系数. 为此，稳态时铜盘P的散热速率的表达式应作面积修正：

(4)

将式(4)代入式(2)即得

(5)

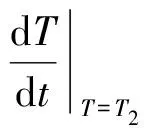
2 稳态法散热面积修正误差分析

实验测量中，稳态时散热P盘的侧面和下表面在散热，上表面与样品接触处于稳态温度没有散热；而在移去样品测量散热盘相同条件下冷却速率时，P盘的散热面为上、下表面和侧面共3个面. 散热面积修正的假定条件是散热P盘的3个面的冷却速率相同，直接进行面积修正得到物体的导热系数. 然而实际情况是由于风扇的鼓风，散热盘的3个面周围空气的扰动不同，因此3个侧面与空气的热传递有差异，直接假定各个面的冷却速率相同进行面积修正有一定的误差，本文利用计算流体软件CFD数值模拟的方法计算冷却盘3个侧面的冷却速率的差异.

2.1 数值模型和边界条件

根据导热系数测定仪的散热盘以及样品的结构尺寸，建立如图2所示的三维计算模型，模型对实验装置进行了简化建模. 其中风扇作为空气的速度入口边界，入口直径为10 cm，入口通道高度为2.5 cm，散热铜盘距离风扇入口9 cm，铜盘的直径为13 cm，厚度为0.7 cm，外围的空气建立以风扇出口中心为圆形的半球体，直径为10倍的铜盘直径130 cm，出口边界使用无穷远边界，环境温度为20 ℃，压强为101 325 Pa，空气为理想气体，铜盘的密度为8 978 kg/m3，比热为381 J/(kg·K)，导热系数为387.6 W/(m·K),辐射系数为0.70，在实验温度范围内假定铜盘的材料属性不发生变化.

图2 散热盘散热的三维数值模型

模型使用CFD软件划分三维数值模拟网格，在散热盘周围的网格为加密网格，远场网格相对稀疏，从而提高计算精度，节省计算时间，计算模型网格数量为573.2万，模型采用SIMPLE算法，湍流模型为Realizable K-ε两方程模型，计算采用瞬态求解方法，时间步长为0.001 s. 因为实验稳态平衡时测得散热盘的温度为34.1 ℃，在数值模拟计算时散热圆盘的初始温度设为44 ℃，高于平衡态10 ℃，在风扇入口速度为1 m/s的风速下进行强迫对流冷却，重点监控(34.1±2) ℃时散热盘3个表面的热流密度.

2.2 数值模拟的结果讨论

图3为计算模型垂直剖面的数值模拟云图分布. 从图3(a)可以看出散热盘铜盘通过风扇鼓风强迫对流冷却，周围的空气温度比风扇入口的温度有了明显上升，大部分区域温度约为20.40 ℃，但散热盘周围的空气温度各个方向分布是不均匀的，散热盘下表面正对冷却来流，温度接近入口温度，散热盘上表面以及上方区域温度相对低，大致为20.15 ℃. 从图3(b)可以得到风扇入口的强迫对流冷却风吹向散热盘后，气流向周围对流扩散，在散热的周围的对流空气中，散热盘的下边缘的对流空气流速最大，达到1 m/s左右，散热盘的下表面中心和上表面的空气对流速度相对较小，只有0.01 m/s左右. 从数值模拟分布的云图可以得到稳态法测量导热系数时，散热铜盘周围的空气流速和温度分布都不同，对流换热强弱的主要影响因素包括物体周围的冷却剂的流动状态和温度分布，因此需要考虑散热盘不同方向上的散热效率的各向异性.

(a)温度分布云图

(b)速度分布云图图3 数值模拟云图

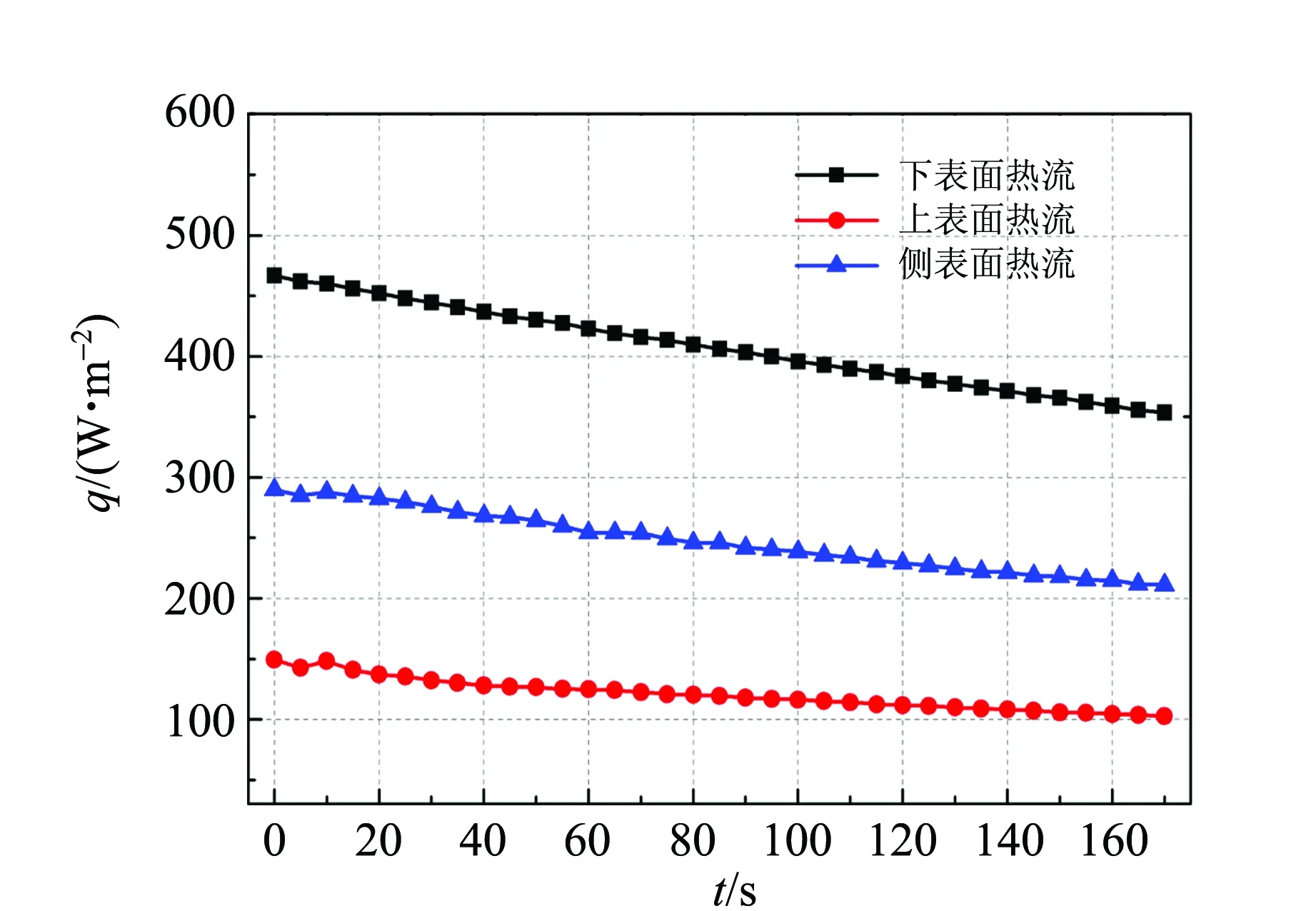
(a)随时间变化曲线

(b)随温度度变化曲线图4 散热盘表面热流密度变化曲线

图4为散热铜盘强迫对流冷却时各个表面的平均热流密度变化曲线图. 从图4(a)和(b)可以看出，散热盘的表面热流密度随着散热盘温度的下降是减小的，但是3个表面的平均热流密度的大小并不相同，特别是上表面的平均热流密度还不到下表面热流密度的一半. 因此在进行散热速率等效时需要考虑各个表面散热的热流密度的差异.

2.3 导热系数计算公式修正

从图4散热铜盘表面的散热热流密度的变化曲线可看出，虽然各个表面的散热热流密度的大小差异很大，但散热盘的3个表面的平均热流密度变化曲线几乎是直线，因此，在实验的测量时间间隔内各个表面的热流密度变化可看成线性变化. 根据采样的数据对3个表面的热流密度随温度变化曲线进行拟合，得到曲线的拟合公式为

(6)

式(6)中T为散热盘的温度，从拟合得到散热热流密度的斜率可以看出3个表面的散热速率不同，其中下表面的散热速率最大，上表面散热速率最小. 由于数值模拟的环境温度为20 ℃，不同的环境温度下冷却的散热热流密度不同，因此对式(6)进行环境温度修正，得到：

(7)

式(7)中Tf为实验室环境温度，利用式(7)对导热系数的求解式(5)进行修正，得到：

(8)

3 结 论

物理实验教学中利用稳态法测量不良导体的导热系数假定散热盘各个表面散热效率相同，计算得到的导热系数存在较大误差，本文利用数值模拟的方式计算得到散热盘在强迫对流换热过程中，散热盘不同表面的平均散热热流密度的差异：

1) 散热盘各表面周围空气的温度和空气流速不相同，导致各表面的散热的热流密度并不相同，其中，下表面散热热流密度最大，其次是散热盘四周表面，最小的是散热盘上表面；

2) 散热盘的散热效率随着散热盘的温度下降而降低，从拟合的曲线斜率来看，散热效率随温度降低的速率最大的是上表面，最小的是上表面；

3) 根据数值模拟的结果，拟合得到不良导体导热系数的修正公式，考虑到散热盘各表面散热效率的差异，减小了实验测量误差.