时变网络下快递员最优投送路线研究——以平江历史街区为例

□ 沈立威，潘 纯，王文佳，孙 琳，范克危

(苏州科技大学,江苏 苏州 215009)

1 平江路历史街区背景条件

平江路于2009年被评为“中国十大历史名街”，与观前街相邻。由于其道路通畅，快递需求较多，极其适合进行研究。平江路主干道西侧为主河流段，东侧靠西为商业街区，靠东为居民区，整体呈矩形，道路较直，研究进行方便。

了解当地街区每条道路的快递需求量并且制定最优的投递路线，不仅能够优化快递服务质量，令客户满意，还节约了快递员的配送时间和精力，减少配送对该街区的道路压力。这样，在提高物流配送水平的同时，也能保证该街区良好的交通情况，实现旅游发展与居民生活的两不误。

2 研究情况

在对平江路各大主要配送路线进行规整后，我们得出了区域道路模拟图(图1)，我们将各点标注上字母，并且记录各条道路行进时所需要的大致时间。

图中，由南向北，d为平江路主入口，A为白塔东路与平江路主路交界处。d至A段为平江路主干道；b为仓街与干将东路交界处，C为白塔东路与仓街交界处，bC段为仓街主路。

由西向东，db为干将东路段；Za为邾长巷；XY为卫道观前、民生巷合路；VW为混堂巷；TU为大新桥巷；OQ为大柳枝巷；MN为丁香巷；FD为胡厢使巷；AC为白塔东路段。

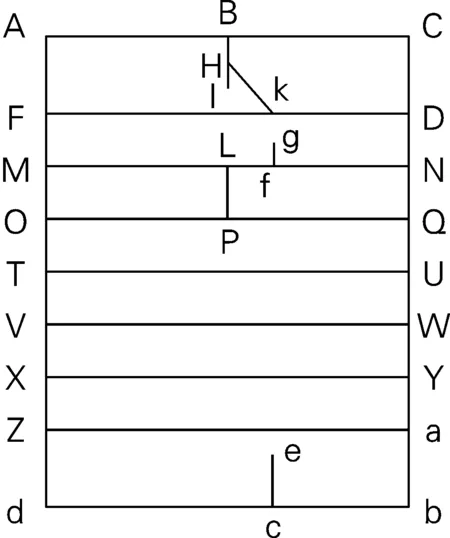
图1 标点后的平江路具体路线

3 方法介绍

“奇偶点图上作业法(graphical method based on an odd-even-point approach)”是解决中国邮路问题的一个重要解决方法，即在某条路线中找到奇点，在奇点之间增加边，令每条边的权和原来的权相等，并把新增加的边称为重复边。

这样就把原问题变为：在一个有奇点的图中，要求增加一些重复边，使新图不含奇点，并且重复边的总权为最小。把使新图不含奇点而增加的重复边，简称为可行(重复边)方案,使总权最小的可行方案为最优方案。

通过对奇偶点图上作业法的延伸，小组实现了平江路快递员投送道路的模型建设，使用Excel工具，将平江路的各条路段规整于一套模型之中，并进行了1500次不同路线模拟。

4 平江路快递需求分析

在路线模拟前，小组还对平江路的快递需求特征进行调查，以图更全面、具体地纵向了解平江路居民快递需求情况。本次发放总计2000份调查问卷，问卷涉及年龄、月收入、最常使用快递价格、使用快递的频率等特征，并且每类特征分为ABCD四个档位，以得出每个年龄段内最常见的组合类型。

最终，小组收集到1768份有效问卷，其中男性812名，女性956名。结合调查统计结果，平江路历史街区的快递使用者中，年龄为18～30岁的人最多，使用频率也最高，年轻一代相对更能接受网络购物。此外，这类人群可以承担6至20元的相对适中的快递费用，符合其收支范围。可见，网络时代的消费主力军依旧为年轻人群，利用好市场，配合良好的服务，快递企业必将能够在投送作业中将成本压缩至最低，收益提升至最高。

5 平江路路段Excel仿真及最优路线分析

5.1 平江路各路段长度数值的随机模拟

结合平江路Excel模型图，在软件中将平江路每段路线的路径长度设置为0单位至10000单位间的随机数值，并且固定(表1)。根据表中数值，路长总和为110886单位。

表1 平江路模型中各路径的模拟长度

5.2 快递员最优投送路线的研究过程

在Excel软件中，模拟1500次快递员不同的投送路线，取其中的两次，比较得出相对最优投送路线的过程如下。

如图2所示，路径总长为142242单位，可以看到重复边为AB、FA、HI、ML、OP、NQ、VT、UW、YX、Zd、dc、cb、ab，重复路长为31356单位。

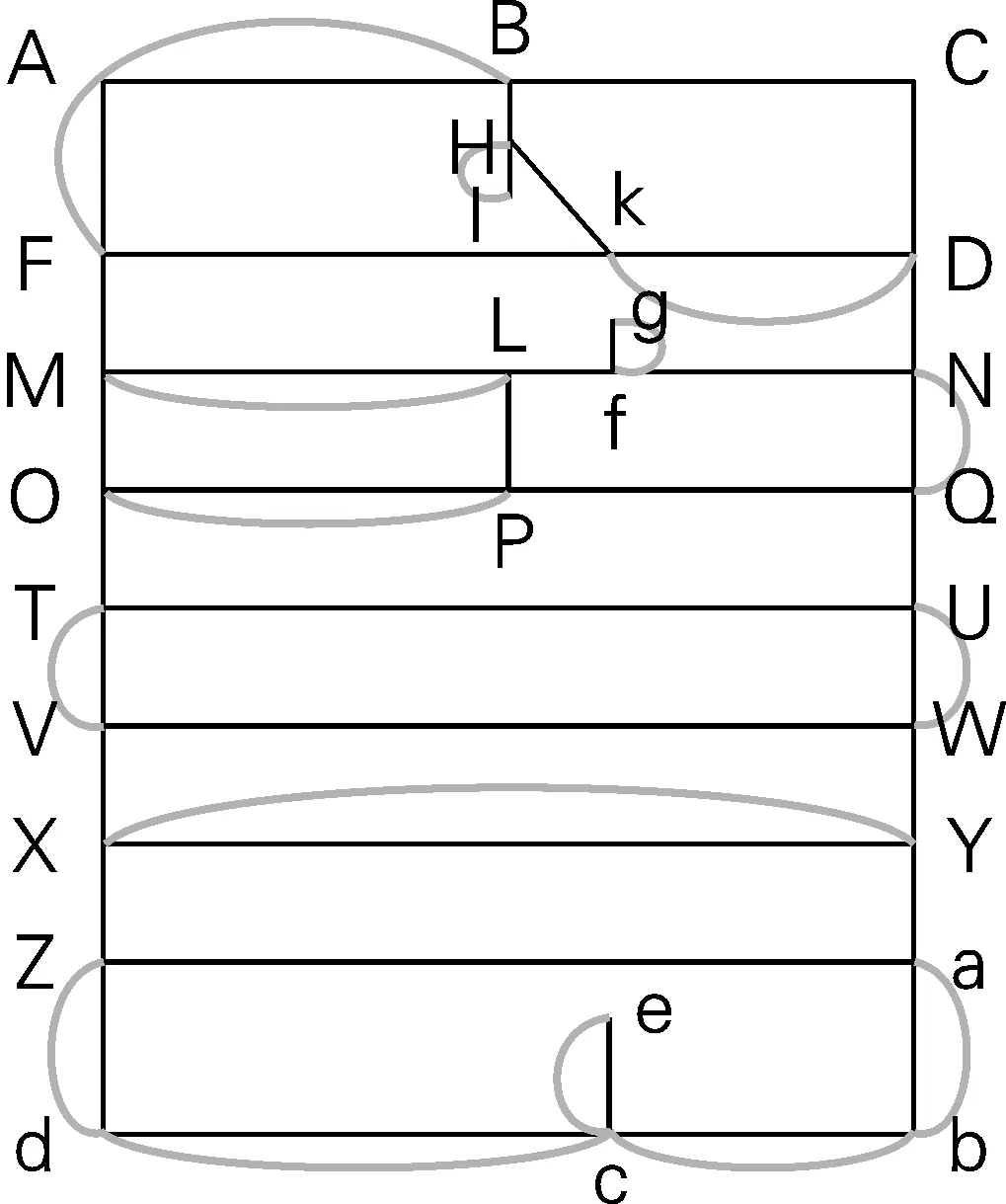
图2 平江路快递投送路线一(相对最优解)

如图3所示，路径总长为142681单位，重复边为AB、FA、HI、ML、OP、NQ、VT、UW、YX、Za，重复路长为31795单位。

图3 平江路快递投送路线二(可行解)

综合上述两种路线，图2相对最优解和图3可行解的区别在于圈Zabd(图4)，检验此圈，最优解虽然重复边更多，但重复边Zd、dc、cb、ab的长度相加比可行解中重复边Za的长度更小，故两解的总长存在439单位的差异。

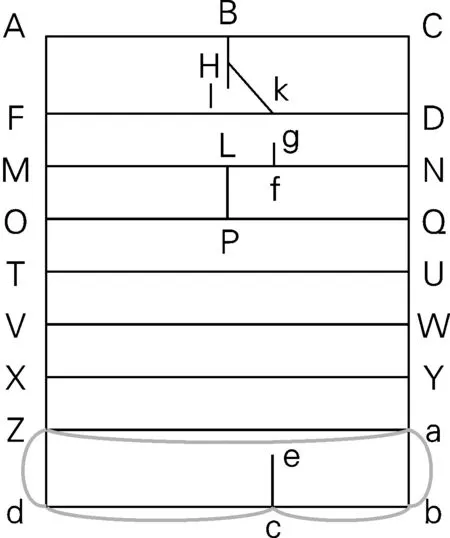
图4 投送路线一、二中的区别圈

5.3 时变条件下最优路线分析

研究前期的快递需求调查显示，不同时间段内，尽管平江路各条主路的需求不尽相同，但多少均有需求。小组在体现时变性方面，结合实际快递需求的分析结果，将无住户、无商家或者需求、可并入其他路段的路线单独提取，设为不固定需求的路线。HE段在居民区内部，该段需求有时可记入BH段；LP为石人弄，需求可计入MN段与OQ段；QU段为不定时经营的杂货铺、UW段为新桥河段上方桥面，需求均不固定。为了避免重复计算，保证后续Excel模型模拟中得出的最优解质量，小组将其需求归为0或1，单独代入计算。0表示没有需求，1表示有需求，则HE、LP、QU、UW四段可以组合出16种情况。比如，四条路都没有需求，则可表示为0000。以此类推，16种情况分别为0000、0001、0010、0011、0100、0101、0110、0111、1000、1001、1010、1011、1100、1101、1110、1111。以0赋值的线段会在图上剔除，此时，我们原本得到的最优解就会发生变化，各不相同。

6 结论

本次课题研究对象为平江路快递员最优投送路线，属于NP问题，即存在多项式算法能够解决的非决定性问题。该问题计算量极大，原始算法为枚举法，即将所有须经路线都串联起来，列举并求和，算出总长后比较，缺乏科学性，也不适合具体操作。使用Excel建立模型具有创新意义，将平江路各条道路具体化，算法步骤也体现出自动性、简洁化。在大量模拟后，能够得出相对最优解，使得快递企业与快递员在平江路具体投送路线的选择上有参考余地。

6.1 快递企业方面建议

当前，国内几乎所有的快递企业都采取分区配送的运作方式，将快递员分区域管辖。区域内情况往往相当复杂，而且各个街道的路况、需求不尽相同。项目结论表明，快递企业需要做好大量的前期准备，首先了解区域内快递需求的详细信息，再进行模拟配送与计算，选取相对最优方案。结合本次模拟研究，快递企业在计算投送路线时，还应当最先考虑该地区的需求，进行需求分析。

6.2 快递员投送方面建议

对于快递员而言，将企业提供信息与实际结合更是关键一环。在熟悉区域后，按照当地道路与特点优化配送环节，能尽快地完成配送工作，一方面节约了自身的配送时间，另一方面，在无形中节约了企业的配送成本，提高运营效率。