液体内部气泡的水平移动问题再探讨*

李陈乐 汪志荣

(安徽师范大学物理与电子信息学院 安徽 芜湖 241002)

中学物理教科书及其配套教辅教材中经常出现有关分析液体内部气泡的运动学问题．例如，装满水的瓶子内有一个气泡，当瓶子突然水平移动时，气泡将怎样运动[1，2]？对此，研究者们多以惯性知识予以解析：当容器突然加速运动时，气泡和液体具有惯性，会往后端移动，由于液体质量远远大于气泡质量，其惯性也会更大，当液体向后运动时会挤压气泡向前端运动，最后得出气泡与容器的运动方向一致的结论[2，3]．实际上，未经分析比较气泡和液体的受力情况，仅仅通过比较两者惯性质量的大小是无法判断各自运动变化快慢的；此外，由于气泡在前后两个方向上均受到来自液体的压力，当容器突然加速运动时，不能直接排除液体将推动气泡向后运动的可能性[4]．然而，比较气泡和液体的受力情况，需要分析气泡前后两侧所受到的液体压力，难度较大，如果选择盛装液体的容器(非惯性系)作为参考系可以简化问题，但会涉及惯性力的概念，还必须运用微积分知识加以分析．中学生尚不具备在非惯性系中对物体进行动力学分析的物理知识基础，也缺乏运用微积分处理物理问题的能力，对该问题一般难以获得较为满意的解释，以下运用类比方法和等效思想对此问题教学策略予以分析探讨．

1 超重现象与“等效重力”概念的提出

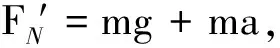
为了方便解决有关超重现象的力学问题，我们也可以选择升降机为参考系，引入“等效重力”的概念加以解释．如图1所示，如果选择升降机作为参考系，此时内部物体即处于静止状态，那么超重现象可以解释为：物体在“等效重力”和升降机的支持力作用下处于受力平衡状态，“等效重力”(可用符号G′表示)和升降机对物体的支持力大小相等，大小即为G′=FN=mg+ma．因此，超重现象也就是物体处于加速运动状态时的“重力”增加的现象，方向与加速度方向相反．如果选择升降机作为参考系，对于处在超重状态或者失重状态的物体，都可以看作它的“重力”发生了变化．假设升降机做匀变速运动时，加速度为a，其内部物体所受“等效重力”的情况分析如下.

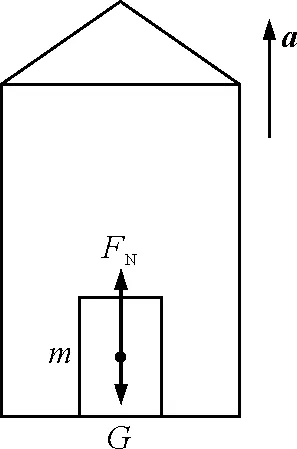
图1 升降机中的超重现象示意图

(1)当加速度a方向向上(加速向上或减速向下)时，其内部物体的“等效重力”即可以看作在原有重力的基础上，向下(加速度的反方向)超重了ma，即G′=mg+ma，考虑到各物理量的矢量性，记G′=mg-ma；

(2)当加速度a的方向向下(加速向下或减速向上，即处于失重状态)时，其内部物体的“等效重力”可以看作在原有重力的基础上向下超重了-ma；也可以理解为：在原来重力的基础上，向上(加速度的反方向)超重了ma，即为G′=mg-ma，考虑到各物理量的矢量性，记G′=mg-ma．

(3)当升降机在水平方向上做加速运动时，如果选择“升降机”为参考系，则其内部物体也可以看作在升降机运动加速度的反方向上“超重”了ma，可以看作物体在水平方向上也具有“等效重力”G′=-ma，如图2所示．

图2 水平“升降机”中的“超重现象”

实际上，只要物体与装载物体的容器共同做加速运动，无论其运动方向如何，如果选择装载物体的容器作为参考系，均可以看作物体在运动加速度的反方向“超重”了ma，因此可根据物体的“等效重力”解决力学问题．

2 液体水平方向上的“浮力”现象

通常来说，浸在液体中的物体会受到竖直向上的浮力，其方向与重力的方向相反．根据流体力学知识，密度为ρ的液体，自重G=mg=ρgV，液体内部压强随深度变化的关系为p=ρgh．对于浸在液体中物体而言，它的各个表面都将受到来自液体的压力，物体受到的浮力实际上就是液体作用在物体上、下表面的压力差，即

F浮=F2-F1=ρgΔhS

其中Δh为物体的上、下表面到液面的深度差，如图3所示．

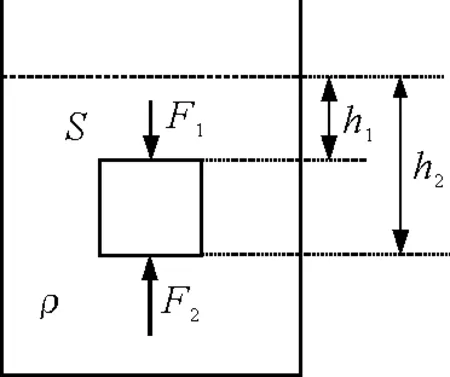
图3 浮力的本质示意图

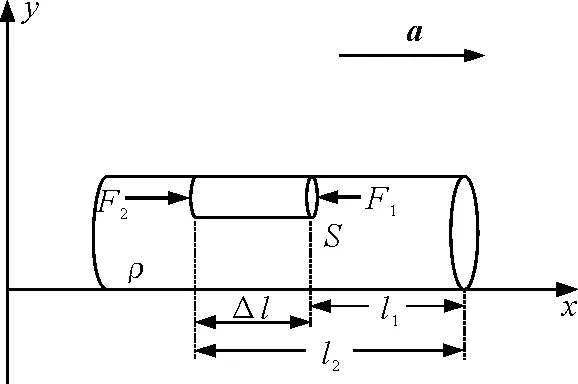
图4 液体内物体受到水平方向的“浮力”示意图

3 液体内气泡的水平移动问题分析

某一容器内装满密度为ρ的液体，沿水平方向向右做加速运动，加速度为a，假设液体内部含有一段密度为ρ′的柱形气泡，气泡的截面积为S，长度为Δl，如图5所示.现在要对该气泡进行动力学分析，同样可以采用类比液体浮力现象进行解析．选择该容器为参考系，当容器在水平方向上做加速运动时，忽略气泡与液体间的粘滞阻力，液体内空气泡会在水平方向上受到“等效重力”以及液体“浮力”的作用．气泡的受力情况具体分析如下.

图5 液体内物体水平方向受力分析示意图

气泡在水平方向上所受到“等效重力”为

G′=-ma=-ρ′aΔlS

(1)

气泡在水平方向所受到液体的“浮力”为

(2)

因此，相对于容器而言，气泡运动的加速度为

(3)

根据式(1)～(3)可得

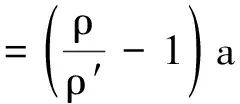
(4)

由式(4)可知，空气柱相对于容器而言，其运动的加速度a相是由液体的密度ρ，空气柱的密度ρ′以及容器自身运动的加速度a共同决定的．由于气泡的密度ρ′远远小于液体的密度ρ，即ρ′≪ρ，因此容器内气泡运动的加速度a相与a方向一致．这说明气泡相对于容器而言，具有水平向右的加速度，因此气泡会向容器前端移动．上述分析结果与通过在非惯性系下对气泡进行动力学分析，并利用微积分等数学工具辅助求解所得气泡的运动规律，是完全一致的[4]．

上述解析液体内部气泡的水平移动问题的基本思路主要表现为：首先，根据超重现象提出“等效重力”的思想，构建解释液体在水平方向上做加速运动时所产生的力学现象的数理模型；其次，通过与液体浮力知识的类比分析，推理出在水平方向上做加速运动的液体同样会对浸在其内部的物体产生“浮力”作用，“浮力”方向与“等效重力”方向相反；最后，基于物体的受力情况，运用牛顿第二定律，分析得出气泡的运动状态．对于液体内气泡的水平移动问题，通过类比重力场中的物体沉浮条件，分析得出水平加速场中的物体“沉浮条件”，分析的结论均是与物体与液体的相对密度以及加速度有关．采用这种教学策略，符合中学生的认知水平及其所掌握的数学知识基础，同时也能够凸显对中学生科学思维能力的培养以及科学方法的教育．

4 结束语

科学思维是物理学科核心素养的重要内容，培养学生的科学思维能力是整个中学阶段物理课程教学的核心任务之一．对于高中阶段学生，我国普通高中物理新课标明确指出，应具有建构理想模型的意识和能力，能够正确运用科学思维方法，从定性和定量两个方面对相关问题进行科学推理、找出规律、形成结论[5]．因此，在此类物理问题解决方面，突出等效思想和类比分析方法的运用，不仅有利于培养学生的科学思维能力，让学生领会该方法在解决物体问题方面能够起到化难为易、简化问题的效果，同时，也进一步深化了学生对液体浮力本质的认识．