2018年高考理综新课标卷Ⅲ第17题的多种解法

刘朝龙

(贵阳市乌当中学 贵州 贵阳 550018)

A.2倍 B.4倍 C.6倍 D.8倍

1 应用平抛运动规律及数学方法求解

解法一：设斜面的倾角为θ，由题意可知两小球平抛过程的位移与水平方向的夹角也均为θ，设小球落至斜面时速度与水平方向的夹角为α，因为

tanα=2tanθ

故两小球落至斜面时速度与水平方向的夹角也相等．

如图1所示，由相似三角形可知

解得v甲=2v乙，故选项A正确．

图1 速度分解

点评：此方法应用平抛运动tanα=2tanθ的二级结论，将速度矢量进行正交分解，再运用数学中两相似三角形对应边比值相等，便可快速而正确地解答此题．

解法二：设斜面的倾角为θ，由题意可知两小球平抛过程的位移与水平方向的夹角也均为θ，设小球落至斜面时速度与水平方向的夹角为α，因为

tanα=2tanθ

故两小球落至斜面时速度与水平方向的夹角也相等．

如图1所示，由三角函数可知

v=v甲cosα

由上面两式解得v甲=2v乙，故选项A正确．

点评：此方法与解法一的区别在于使用的数学工具不同．前者应用的是相似三角形，而后者运用的数学知识是直角三角形中的余弦函数．

解法三：设斜面的倾角为θ，由题意可知两小球平抛过程的位移与水平方向的夹角也是均为θ，设小球落至斜面时速度与水平方向的夹角为α，因为

tanα=2tanθ

故两小球落至斜面时速度与水平方向的夹角也相等．小球落至斜面时，设甲、乙两小球在竖直方向的速度大小分别为vy甲,vy乙．

如图1所示，由三角函数可知

vy甲=vtanα

根据勾股定理有

联立解得v甲=2v乙，故选项A正确．

点评：此方法与解法二相比，区别也是数学工具：将解法二的直角三角形的余弦函数换为正切函数，同时运用勾股定理联立解答．

解法四：由题意可知，两小球平抛过程的位移与水平方向的夹角相等，设甲、乙小球平抛运动的时间分别为t甲和t乙．由图可知，两小球的水平位移大小与竖直位移大小之比相等．

根据平抛运动的规律，有

解得

t甲=2t乙

小球落至斜面时，设甲、乙两小球在竖直方向的速度大小分别为vy甲，vy乙．根据平抛运动的规律vy=gt可知

vy甲=2vy乙

由于落至斜面时，小球甲速度的水平分量和竖直分量都是小球乙速度的水平分量和竖直分量的2倍，说明两小球的水平速度与竖直速度构成的两个直角三角形相似．由相似三角形规律可知斜边也是2倍，即

v甲=2v乙

故A选项正确．

当然，此解法得出vy甲=2vy乙结论后，也可以直接应用勾股定理得出v甲=2v乙．

点评：此方法是一种常规解法，也是大多数考生采用的方法．需要考生熟练地掌握平抛运动的基本规律，熟知解答平抛运动采用的矢量分解法及相关的数学知识．

2 应用动能定理及能量守恒定律求解

解法五：由题意可知，两小球平抛过程的位移与水平方向的夹角相等，设甲、乙小球平抛运动的时间分别为t甲，t乙．由图1可知，两小球的水平位移大小与竖直位移大小之比相等．

根据平抛运动的规律，有

解得t甲=2t乙.

h甲=4h乙

设甲、乙两小球的质量均为m，由动能定理得

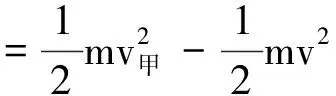
联立解得v甲=2v乙，故选项A正确．

点评：动能定理是一个重要的物理规律，在中学物理中有着广泛的应用，是高中阶段处理物理问题的主要学科思维之一．使用此方法能够彰显考生的学科素养，同时也显示出对物理知识的综合应用能力．

解法六：由题意可知，两小球平抛过程的位移与水平方向的夹角相等，设甲、乙小球平抛运动的时间分别为t甲，t乙．由图1可知，两小球的水平位移大小与竖直位移大小之比相等．

根据平抛运动的规律，有

解得t甲=2t乙.

设小球落至斜面时，甲、乙两小球下落的高度分别为h甲，h乙，由平抛运动的规律

可知

h甲=4h乙

设甲、乙两小球的质量均为m，所以，平抛过程中小球甲重力势能的减少量是小球乙重力势能的减少量的4倍，根据机械能守恒定律可知，小球甲动能增加量是小球乙动能增加量的4倍，即

联立解得

v甲=2v乙

故A选项正确．

点评：能量守恒定律是一切物理过程遵循的基本规律．能量守恒应该是贯穿整个物理学的一个重要理念，它不仅仅是某一两个章节的内容．因此，在高三备考复习中，应该引导学生构建完备的物理学科知识体系．

3 运用动量定理求解

解法七：若小球运动过程中初、末动量分别为px，p，落至斜面时，竖直方向的分动量为py，根据动量定理有

I=p-px

根据矢量运算法则，由图2可知

py=p-px

即

I=py

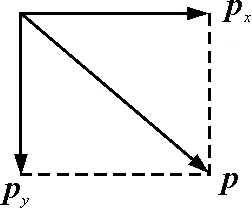
图2 动量分解

设甲、乙小球质量均为m，平抛运动的时间分别为t甲，t乙，甲、乙两小球在竖直方向的速度大小分别为vy甲，vy乙，则可得

mgt甲=mvy甲

mgt乙=mvy乙

根据平抛运动的规律，由三角函数可知

联立解得

vy甲=2vy乙

由于落至斜面时，小球甲速度的水平分量和竖直分量都是小球乙速度的水平分量和竖直分量的2倍，根据勾股定理可知

v甲=2v乙

故A选项正确．

点评：动量定理是选修3-5内容，在2017年以前属于选考模块，受到诸多因素的制约，动量定理的相关内容与动力学的综合较少，师生的重视程度不够．而且，在矢量运算中，三角形法则的应用没有平行四边形法则的应用广泛，故这种解法在以上7种方法中较生僻．

教学启示：本题在2018年高考理综新课标卷Ⅲ物理试题中难度中等，题干简洁，考查的方法多样，留给学生发散的思维空间较大，属于一题多解的试题．从高考选拔功能的角度看，此题是一道好题．一题多解，是指对一道习题，采用多种方式求解．由于所用的物理规律及方法不同，可以实现从多个侧面深入认识和理解同一运动规律．此题的一题多解，涉及平抛运动的规律、牛顿运动定律、动能定理、机械能守恒定律、动量定理及各种数学方法．因此，在物理教学中要注意锻炼学生一题多解的能力，尤其是在高三复习备考中，多尝试此类习题，既能巩固不同的物理知识和规律、方法和技巧，同时也能培养学生的发散思维和创新能力，激发学生学习物理的兴趣和对问题探究的欲望．