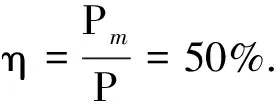磁力小火车驱动原理及速度影响因素分析

张适

(北京市育英学校 北京 100036)

在第七届中国大学生物理学术竞赛中有这样一道题目：两个扁圆柱形磁铁与一个柱状的电池两端相接，当这个体系放在铜线圈内部且与铜接触的时候，它会开始运动．解释这个现象并且研究相关参量怎么影响火车的速度和功率．

题目中的小实验材料简单、制作简易，效果明显，充分展现了电磁驱动现象，引发了不少学生和教师的关注和讨论，这道题目也曾作为北京市中学生物理学术竞赛的一道题目．笔者观看了参赛小组对本题目的研究汇报发现，在解释小火车的运动原理时，都引用了“磁力小火车的驱动原理”一文的分析方法，即将磁铁的磁性解释为分子磁矩和等效环形电流[1]，这种方法有效地解释了小火车的驱动原因；在研究相关参量影响小火车的速度时，参赛小组应用控制变量法，从铜线长度、螺线圈横截面积、线圈匝数、电池节数、磁铁数以及电池连接方式等方面进行了实验探究，并作了相应的解释，取得了较好的效果．笔者认为，在一些实验现象的分析和原理的解释中仍有不完善之处，有必要作进一步探讨．如，磁力小火车的驱动原理还有什么方法分析？小火车的动力和阻力究竟有哪些，与什么因素有关？小火车启动后为什么会达到一个恒定的速度？小火车的最大速度和功率与哪些因素有关？本文试图对以上问题作一些分析，不当之处望同行批评指正．

1 驱动原理分析

通过实验发现，磁铁吸附电池的方式中，只有如图1中的两种方式才会使电池运动．当电池正负极都与磁铁N极相连，即正(N)负(N)型，这种情况下电池向右运动；当电池正负极都与磁铁S极相连，即正(S)负(S)型，这种情况下电池向左运动．如果改变线圈的绕行方式或改变电池的放置方向，能运动的仍然是这两种方式，只不过电池运动的方向会发生改变，这说明螺线管的绕向与电池能否运动无关．小火车的驱动原理和运动方向的原因，也可以通过以下两种方法解释．

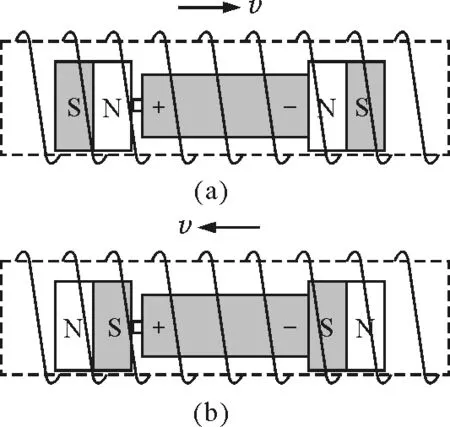
图1 磁铁吸附电池的两种方式

方法1：以图1(a)为例，电池在螺线管中某处时，电池通过左端磁铁A和右端磁铁B及它们之间的铜导线圈连成一导电回路，其电流如图2所示．

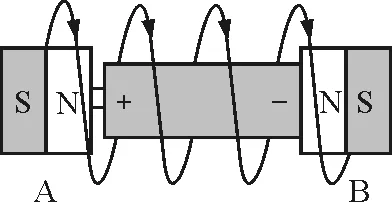
图2 电池通过两端磁铁及之间导线圈连成一回路

沿螺线轴线方向取一截面，两磁铁在通电导线处产生的磁场如图3所示.根据左手定则可判断出靠近A处的导线所受的安培力方向呈向左发散状，如F1，F2，F5，F6其合力向左，靠近B处的导线所受的安培力方向呈向左汇聚状，如F3，F4，F7，F8其合力也向左，故A，B间的铜线圈所受的合力方向向左．根据牛顿第三定律知，当铜线圈不动时，磁铁和电池组合体就会受到向右的动力，当动力大于阻力时就会向右运动．

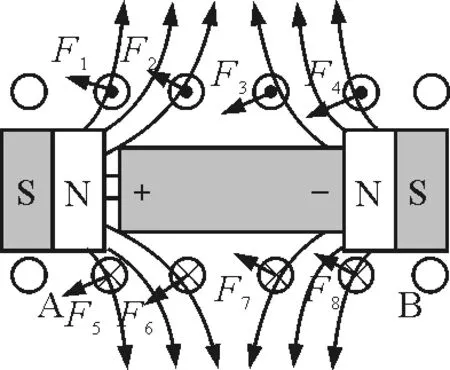
图3 靠近A,B处导线所受安培力情况

方法2：仍以图1(a)为例，电池在螺线管中某处时，两磁铁A与B间通电螺线管产生的磁场如图4所示．

图4 通电螺线管产生的磁场

由于靠近电池的正极和负极处的磁场较强，所以靠近电池的磁极所受的力较大，A，B两磁铁的N极和S极所受磁力情况如图5所示.A磁铁的N极受到向右的磁力FAN大于S极受到向左的磁力FAS，合力向右，B磁铁的N极受到向右的磁力FBN大于S极向左的磁力FBS，合力也向右，显然电池和两磁铁组合体所受的合力方向向右，当这个合力大于组合体所受的阻力时，就会向右运动．

图5 A，B两磁铁N，S极所受磁力情况

2 受力分析

实验表明，最初小火车由静止开始做加速运动，而后很快就达到最大速度保持恒定的速度匀速运动.从力与运动角度分析，加速运动过程中，驱动力大于所受的阻力；达到最大速度时，驱动力等于所受阻力．从加速到匀速，小火车所受的驱动力和阻力应至少有一个发生变化，才能使合外力逐渐减小至零，那么，是什么力发生了变化？

2.1 驱动力分析

驱动力是铜线圈产生的磁场与A，B磁铁间的相互作用力，这个力由线圈中的电流大小和A，B磁极的磁场强弱决定．以图4为例，当小火车静止时，由于前后两个磁极相同，它们在A，B段铜线管中的磁通量始终为零，并不产生感应电动势；当小火车向右运动时，对A，B段铜线圈而言，A磁铁进入线圈，使线圈向右的磁通量增大，B磁铁离开线圈，使线圈向左的磁通量减小．由楞次定律可判断出，在该段线圈中产生与原电流方向相反的感应电动势 (反电动势)．以图3为例，若用Bi表某匝线圈处的磁感应强强度，θi表示磁感线与该匝线圈平面的夹角，用n和d分别表示A，B段铜线圈的匝数和横截面直径，v表示小火车的速度，则反电动势可表示为

(1)

若用E，r分别表示电池的电动势和内电阻，R表示A，B段铜线圈的电阻，由闭合电路欧姆定律可得A，B段铜线圈中的电流为

用Fi表示所受的安培力，由如图6所示可求得A，B段铜线圈所受磁铁的作用力为

图6 A，B段铜线圈所受到磁场的作用力

根据作用力与反作用力，可得小火车所受的驱动力为

(2)

由式(1)、(2)分析可知，随着小火车速度的增大，反电动势增大，电流减小，驱动力逐渐减小，当速度恒定时，驱动力也达到恒定值．

2.2 阻力分析

摩擦阻力.由Ff=μFN知，小火车前进时所受铜线圈的摩擦阻力大小应与车重和接触面处的动摩擦因数决定，其大小为Ff=μmg，其中μ为磁铁和电池与铜线圈间的动摩擦因数，m为磁铁和电池的总质量．当铜线圈水平放置且绕制的疏密程度相同时，组合体的重量不变，摩擦阻力大小基本不变．

空气阻力.小火车前进所受空气阻力虽然与车速有关，但小火车的速度又较小，这个阻力是很小的，可以不考虑．

电磁阻尼.以图4为例，当小火车前进时，电池两端的A磁铁靠近通电铜线圈产生的磁场，B磁铁远离通电铜线圈产生的磁场，使得穿过A，B磁铁截面的磁通量发生变化，从而在A，B截面上产生感应电流(涡流)，并受到阻碍运动的力．电磁阻尼力无法定量表达，我们可以进行简化处理，将磁铁简化为一等效金属圆环，其直径为dj，等效电阻为Rj，若用Bj表示通电铜线圈在该环处的磁感应强度，α表示Bj与环面的夹角，如图7所示.

图7 将磁铁简化为等效金属圆环

当小车以v向右运动时，环切割磁感线，产生感应电动势为

Ej=Bjπdjvcosα

感应电流为

所受的电磁阻力为

(3)

可见，随着车速的增大，电磁阻力增大．运动中，由于磁铁和通电线圈相对静止，穿过两磁铁的磁通量没有明显变化，所以这个电磁阻尼力较小，也可以不考虑．

3 最大加速度和最大速度分析

3.1 启动条件及最大加速度

若用FD表示驱动力，Ff表示阻力，不考虑空气阻力和在磁铁中产生的电磁阻尼力，m,a分别表示小火车的质量和加速度，由牛顿第二定律可得

FD-Ff=ma

(4)

由式(4)可知，若要想使小火车启动时，须有FD>Ffm，Ffm为最大静摩擦力，通常取Ffm=μ0mg(μ0为静摩擦因数)；运动开始时，速度v=0，FD最大，由式(1)和式(2)和得最大驱动力为

启动的条件为

(5)

实验表明，对磁铁、线圈材料、电池都有一定要求，一般取一节普通的南孚7 号电池、4～10片直径12 mm圆柱形钕铁硼超强磁铁、直径约1 mm的铜线绕制的螺线管，完能较好地成实验．

小火车启动后加速运动的加速度可由式(4)求出

小火车刚启动时，速度v=0，I最大，由以上各式可得最大加速度为

(6)

3.2 最大速度及影响因素

小火车启动后，v增大，FD减小，加速度a减小；当a=0时，FD减小到最小值，v达到最大值，由式(1)、(2)、(4)联立可得最大速度为

(7)

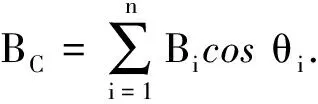
由式(7)分析可知，影响小火车运动速度的因素有A,B磁铁的磁性强弱、体积大小、材质、质量和个数，电池的电动势、内阻、质量，铜线圈的粗细、铜丝的粗细、绕制的松紧程度(A,B间的匝数)，A,B磁铁与铜线圈间的动摩擦因数等．在这些因素中，动摩擦因素μ越小、电池的电动势E越大，A,B间铜线圈和电池的内电阻越小，磁铁和电池的总质量m越小，小火车的速度越大．对于式中的dBC，则需要分情况讨论．

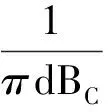
条件下，分析如下：

时，vm有最大值，为

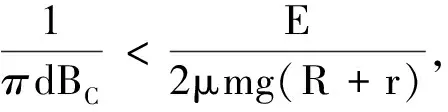
时，随着πdBC的增大，vm减小；

时，随着πdBC的增大，vm增大．

其他因素对速度v的影响都是双重的，如增加磁铁的对数时，磁性增强了，利于增大驱动力，但在线圈中产生的反电势也增大了，磁铁和电池的总质量增大，也增大了摩擦力；增加A，B间铜线圈的匝数时，也同时增大了反电动势，减小了铜丝的横截面，增大了导线的电阻，同时增大了磁铁中产生的涡流．

需要说明的是，以上表达式，是简化了的物理模型，只能说明影响速度的相关因素有哪些，并不能完全反应实际情况，特别是影响速度的某些因素究竟对速度有何影响，必做进一步定量测算和分析．

4 功率分析

由式(1)和式(7)两式可求得：小火车匀速运动时，在铜线圈中产生的反电动势和回路电流分别为

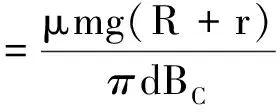
(8)

电源提供的总功率和回路消耗的热功率分别为

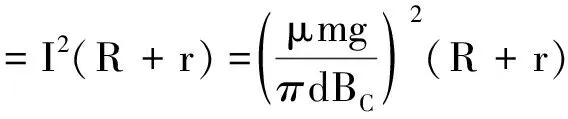
(9)

小火车的机械功率为

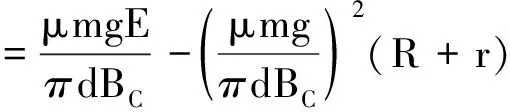
(10)

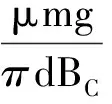
P机最大，为

(11)

此时电源提供的总功率、回路消耗的热功率分别为

(12)

可见

IE=IE反+I2(R+r)

由此，可得出如下结论：

(1)从能的转化和守恒角度说，正是这个反电动势的存在，才使得电池消耗电能的一部分转化为小火车的机械能．

(2)小火车的最大机械功率仅由电源的电动势和回路总电阻决定，这也是机械功率的理想最大值．