“盘点”实数中的易错点
2019-12-28 01:57文步红艳
初中生世界 2019年46期
文步红艳
一、概念不清
例1 在实数0.1212,,π0中,无理数的个数是( )。
A.0个 B.1个 C.2个 D.3个
错解:选C或D。
错因剖析:对有理数和无理数的概念混淆不清,无理数是无限不循环小数。
正解:选B。
变式:在实数,0.1212…,
中,有理数的个数是( )。
A.0个 B.1个 C.2个 D.3个
正确答案:D。
二、审题不清
例2的算术平方根是( )。
A.8 B.4 C.2 D.-2
错解:选A或选B。
错因剖析:观察不细致,乍一看,特简单,思维比手算还快,跳了步骤,易误选B。因为,所以应是的算术平方根,而非16的算术平方根。
正解:选C。
变式:的算术平方根是( )。
A.8 B.4 C.2 D.1
正确答案:C。
三、带分数的计算出错
例3 计算
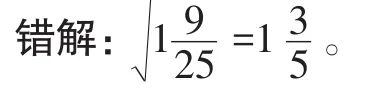
错因剖析:求带分数的平方根(算术平方根)时,应和乘除计算一样,先将带分数化为假分数,再求其平方根或算术平方根。
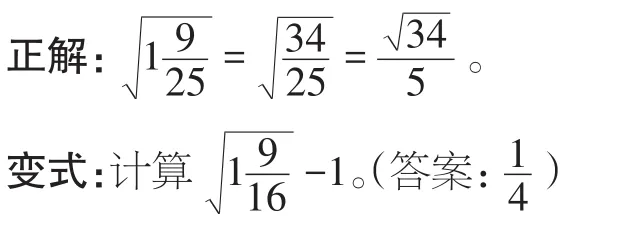
四、数形结合出错
例4 如图1,在数轴上,-1、的对应点表示为A、B,点B关于点A的对称点为点C,则点C表示的数是( )。

图1

错解:选B或选C。
错因剖析:对称轴上线段的表示发生错误,从而不能正确表示数轴上的无理数。
正解:因为A、B表示-1、,所以
我们应在全面掌握平方根或算术平方根概念的基础上,再进行化简和计算。只有对实数概念把握清晰了,并能进行辨析,克服“会而不对,对而不全”的问题,才能避免错误的发生。
猜你喜欢
中学生数理化·七年级数学人教版(2021年11期)2021-12-06
初中生世界(2020年46期)2021-01-05
中学生数理化·七年级数学人教版(2020年3期)2020-08-10
初中生世界·九年级(2020年2期)2020-04-10
初中生世界·七年级(2019年8期)2019-08-29
作文通讯·初中版(2017年11期)2018-03-31
小天使·二年级语数英综合(2017年9期)2017-10-20
小雪花·小学生快乐作文(2016年12期)2017-03-08
小天使·一年级语数英综合(2016年5期)2016-05-14
中学生数理化·七年级数学人教版(2014年2期)2014-06-20

