根区导灌条件下土壤水分分布特性模拟研究

吕 棚 棚

(山西省水利水电科学研究院，太原 030002)

0 引 言

近年来，随着人们生活水平的提高，水果的需求量不断增加，果树的种植面积也不断扩大，但是很多果树种植在水资源缺乏的北方山丘区，采用传统地面灌溉进行灌水，土壤水分蒸发损失较大，水分生产率较低。因此，如何降低棵间土壤蒸发损失，提高水分生产率，是该地区果树生产可持续发展的关键。根区导灌技术是通过埋在根区深层土壤中的导灌器，将水分直接补充到作物的根系部位，实现由灌溉土壤到灌溉作物的根本转变，减少了地面的无效蒸发和灌水器的堵塞，提高了灌溉水利用效率[1,2]。研究表明对于葡萄、柑橘采用根区导灌灌溉，可以减少灌水量、提高水分利用率增加果树产量[3,4]。实际中果树的种类较多，种植模式不同，需要根区导灌的布置方式也不同，而根区导灌的布置方式又是根据根区导灌的土壤水分分布特性来设计的，所以研究根区导灌土壤水分分布特性十分必要。随着计算方法和计算机技术的发展，数值模拟在土壤水分运动研究中得到了大量的应用，相比物理试验具有省时、省钱、 便于模拟各种工况等优点[4-9]。因此，本文将采用数值模拟的研究方，对根区导灌土壤水分分布特性进行研究，以期为根区导灌的合理布置提供技术支持。

1 材料与方法

1.1 试验土壤

试验土壤采自山西省水利水电科学研究院节水示范基地的0～40 cm土层，土壤质地为黏壤土，土壤容重为1.48 g/cm3，饱和含水率为0.458 cm3/cm3，田间持水率为0.295 cm3/cm3。

1.2 试验装置与观测项目

根区导灌土壤水分运动试验装置由土箱、导灌器和马氏瓶三部分构成，马氏瓶用来给导灌器供水，土箱的制作材料为厚1 cm的有机玻璃板，土箱长0.8 m，宽0.8 m，高1.5 m。导灌器为1/4圆柱型灌水器，直径为20 cm，长度为40 cm，导灌器侧壁布置有直径为1 mm的灌水孔，底部和顶部为不透水有玻璃板，且顶部用输水管和马氏瓶连接，如图1所示。试验时，导灌器放置在土箱一角，埋在土面以下20 cm处，由马氏瓶通过输水管向导灌器供水，灌溉水通过导灌器管壁渗入土壤。试验开始时，采用秒表计时，并在不同时刻记录马氏瓶读数，得到试验灌水量，试验结束后，采用小土钻每10 cm取一层土，烘干法测定土壤含水率。

图1 试验装置示意图

2 根区导灌条件下土壤水分运动模型

2.1 控制方程

根区导灌的导灌器为一圆柱型灌水器，水分通过导灌器渗入根区土壤，所以根区导灌的土壤水分运动可简化为二维轴对称问题研究，如图2所示。图2中EFGH为导灌器，DE、AH为中心轴，BC为计算区域的右边界，CD为计算区域的下边界，AB为计算区域的上边界。在柱坐标系下，土壤水分运动控制方程为：

(1)

式中：h为负压水头，cm；θ为土壤体积含水率，cm3/cm3；K(h)为非饱和土壤的导水率，cm/min；t为时间，min；r,z为平面坐标，规定z轴向上为正，cm。

图2 根区导灌计算区域图

2.2 初始条件

h(r,z,t)=h0(r,z),t=0

(2)

式中：h0(r,z)为与初始含水率相对应的负压水头，cm。

2.3 边界条件

(1)边界AB，即土壤表面边界，由于室内试验时间较短，忽略土壤蒸发，该边界为零通量隔水边界，即：

(3)

(2)下边界DC和右侧边界BC，由于计算域选取较大，故为第一类边界条件处理。即：

右侧边界BC：h(rmax,z,t)=h0(rmax,z),t>0

(4)

下边界DC：h(r,zmax,t)=h0(r,zmax),t>0

(5)

式中：rmax，zmax为计算区域的右侧计算边界和下侧计算边界，cm。

(3)边界DE和AH，为柱坐标对称轴，故为零通量边界。

(6)

(4)FG为水分的入渗面，在灌水阶段，由于导灌器内始终存在水头，故应考虑压力势。 即：

h(r0,z,t)=hi

(7)

式中：r0为导灌器半径，cm；hi为导灌器水压力，cm。

(5)EF和HG为隔水边界，水流通量为零，即：

(8)

2.4 模型参数与模型求解

土壤水分运动模型参数采用van Genuchten[10]模型表示：

(9)

(10)

其中Se=(θ-θr)/(θs-θr)

式中：θr,θs分别为土壤残余含水量和饱和含水率，cm3/cm3；Ks为土壤饱和导水率，cm/min；α、n、m为经验参数，m=-1/n，n>1。 采用压力膜仪测定土壤水分特征曲线，TST-55A型渗透仪测定饱和导水率，参数θr、θs、α、n、Ks，分别为0.048 cm3/cm3、0.458 cm3/cm3、0.008 75、1.703 2、0.008 51 cm/min。

求解土壤水分运动方程的数值方法有有限差分、有限元和有限体积法，由于有限元法方便处理各种复杂边界，在数值计算中得到了广泛应用，所以本文采用有限元法进行求解，采用VB.net进行编程[11]。

2.5 模型精度评价指标

为了合理评估模型的预测性能，本文采用平均决定误差MAE、平均相对误差MRE和均方根误差RMSE三个评价指标对模型进行评价，其计算公式分别为：

(11)

(12)

(13)

式中：θs为根区导灌模型计算土壤含水率，cm3/cm3；θR为根区导灌试验实测土壤含水率，cm3/cm3；n为实测土壤含水率点的总数。

3 结果与分析

3.1 根区导灌条件下土壤水分动模型验证

图3为根区导灌土壤水分模拟与实测对比图。由图3可知，根区导灌条件土壤水分随着深度的增大，呈先增大后减小的变化趋势，距导灌器越近，土壤含水率越大。图中实线代表模型模拟值，圆点代表试验实测值，由图可知土壤含水率的模拟值和实测值变化趋势一致，且吻合较好。采用SPSS20对土壤含水率模拟值与实测值进行相关性分析，含水率模拟值与实测值相关性如图4所示，相关性方程斜率为1.011 3，相关系数为0.985 9，在0.01水平下显著相关，这充分说明了模拟值与实测值之间具有较好的一致性。并进一步计算模型得到平均绝对误差MAE为0.01 cm3/cm3，平均相对误差MRE为4.96%，均方根误差RMSE为0.013 cm3/cm3。由此可见，本研究建立的根区导灌条件下土壤水分运动模型具有较高的精度，可以用于计算根区导灌条件下土壤水分运动。

图3 根区导灌土壤水分模拟与实测对比图

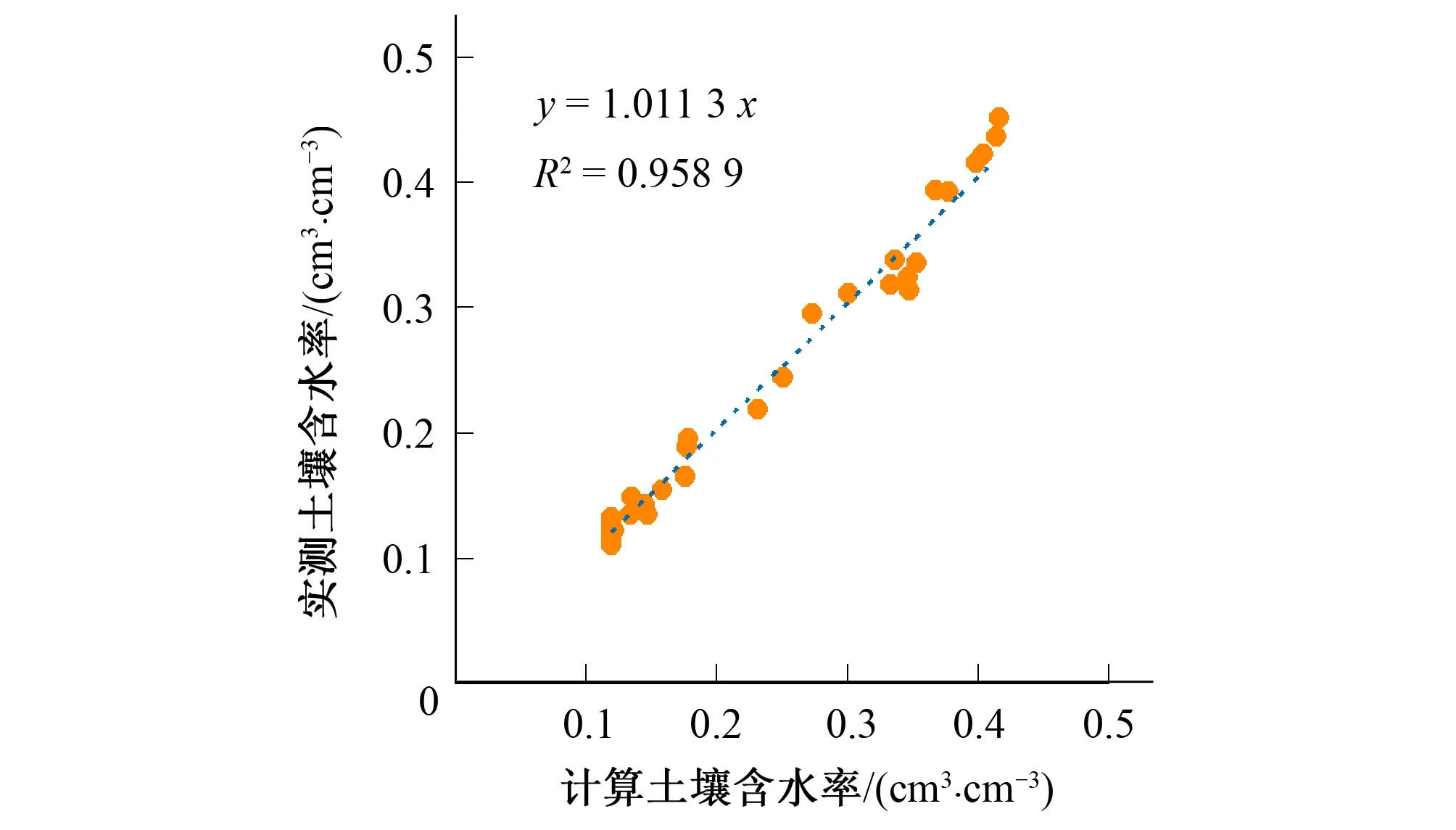
图4 根区导灌土壤水分模拟与实测值相关分析图

3.2 根区导灌条件下导灌器长度对土壤水分分布的影响分析

在验证根区导灌土壤水分运动模型的基础上，采用根区导灌土壤水分运动模型计算了不同导灌器参数(导灌器长度为30、40、50 cm和导灌器直径10、20、30 cm)对土壤水分分布的影响。图5中导灌器长度分别为30、40、50 cm，直径均为20 cm，灌水结束时的土壤水分分布图。由图可知，不同导灌器长度条件下土壤水分分布相似，均是以导灌器为中心的椭球状分布，距导灌器越远，土壤含水率越小。进一步分析可知，导灌器长度对土壤水分的分布范围有一定的影响，导灌器长度越长，土壤水分在垂直方向分布越深，在水平径向分布越近。50 cm和40 cm长的导灌器分别比30 cm长的导灌器，在垂向分布深度增加8 cm和4 cm，在水平方向减小4 cm和2 cm。

3.3 根区导灌条件下导灌器直径对土壤水分分布的影响分析

图6为导灌器直径分别为10、20、30 cm，长度40 cm，灌水结束时的土壤水分分布图。由图6可知，不同导灌器直径条件下土壤水分分布相似，均是以导灌器为中心的椭球状分布，距导灌器越远，土壤含水率越小。进一步分析可知，导灌器直径对土壤水分的分布范围有一定的影响，导灌器直径越大，土壤水分在垂直方向分布越浅，在水平径向分布越远。导灌器直径为30 cm和20 cm分别比导灌器直径为10 cm，在垂向分布深度减小4 cm和2 cm，在水平方向增加2 cm和1 cm。

图5 不同导灌器长度条件下土壤水分分布图

图6 不同导灌器直径条件下土壤水分分布图

4 结 论

(1)根据根区导灌土壤水分运动特点，建立了根区导灌条件下土壤水分运动数学模型，并采用室内试验对模型进行验证，结果表明模型计算的土壤水分分布与试验值一致，模型的平均绝对误差、平均相对误差和均方根误差分别为0.01 cm3/cm3、4.96%和0.013 cm3/cm3，说明本文所建的模型具有较高的模拟精度，可用于根区导灌土壤水分分布模拟。

(2)采用根区导灌土壤水分运动模型，对不同导灌器长度和直径对根区导灌土壤水分分布特性的影响进行模拟，结果表明根区导灌条件下土壤水分分布以导灌器为中心，呈椭圆状分布。导灌器长度越长，土壤水分在垂直方向分布越深，在水平径向分布越近。导灌器直径越大，土壤水分在垂直方向分布越浅，在水平径向分布越远。