基于三支决策改进TOPSIS的水资源承载力评价

孙国营，孙新杰，霍兴赢，龙尚银

(六盘水师范学院数学与信息工程学院，贵州 六盘水 553004)

水是生命之源，我国的水资源分布很不均衡，加上人口的增加、生态资源的破坏等原因，我国一些地区已经成为水资源匮乏的区域。水资源承载力是水资源可持续利用的重要指标，水资源承载力的研究对区域水资源的优化配置和合理应用有着非常重要的作用。

关于水资源承载力的评价已经有很多的研究。如危文广[1]的基于理想点法的江西省水资源承载力评价；袁艳梅[2]的改进的模糊综合评价法在水资源承载力评价中的应用；王正选[3]的基于改进模糊集对评价法的水资源承载力评价----以龙川江流域为例；许有鹏[4]的干旱地区水资源承载能力综合评价----以新疆和田河流域为例；陈腊娇[5]的主成分分析法在水资源承载力影响因子评价中的应用；党丽娟[6]的水资源承载力研究进展及启示；左其亭[7]的水资源承载力研究方法总结与再思考；李高伟[8]的基于主成分分析的郑州市水资源承载力评价。

关于水资源承载力评价的文献远不止于此，前期研究也有比较丰硕的成果，但是也存在一些局限性：对水资源承载力的评价仅局限于所获评价指标数据的基础上，如果有个别评价指标的数据出现异常，就有可能会使该水资源承载力的排名产生较大的影响。因此，本文引入了三支决策的评级制思想，通过主观评判，给不同的评价指标值进行打分，再结合TOPSIS算法进行评价，可以在最大程度上减少个别数据的干扰。另一方面，传统的评价方法只有排名，而不能体现类别，因此，本文根据获得的排名结果和三支决策的阈值α和β，将最终的水资源承载力分为优、良、差三个等级，便于人们更加直观的观察。

1 构建评价指标体系

为了能够准确、科学的判断水资源承载力的排名和级别，从水资源、生态环境、经济和社会4个方面进行考虑，并选取人均水资源量、水资源开发利用率、人均日生活用水量以及人口密度等15个属性作为评价指标，建立了水资源承载力评价指标体系，如表1所示。

表1 水资源承载力评价指标体系

2 数据标准化处理

2.1 创建初始矩阵

假设一共有m个水资源承载力对象，每一个对象内有n个属性，用mij表示水资源承载力初始矩阵M中第i个对象下的第j个属性，构建水资源承载力初始矩阵M如下：

(1)

2.2 标准化处理

标准化处理的目的是将不同评价指标的数据划到同一量级上。效益型和成本型的数据标准化处理的公式各不相同，分别通过下式获得标准化决策矩阵X=(xij)m×n：

对越大越好的效益型指标[9]，原始数据标准化处理的公式如式(2)：

(2)

对越小越好的成本型指标[9]，原始数据标准化处理的公式如式(3)：

(3)

3 计算权重

3.1 标准差贡献率法[10]计算客观权重

(1)获取mij在第i个评价指标中的占比，如式(4)所示：

(4)

(2)获取第j个评价指标的权重μj，如式(5)所示：

(5)

(3)获取客观权重向量W1，如式(6)所示：

W1=(μ1,μ2,μ3,…,μn)T

(6)

3.2 计算主观权重

群决策相对熵集结模型是对多个目标进行评判决策的主观权重赋权方法[11]，具体如以下三步所述：

(1)计算群组决策矩阵K，如式(7)所示：

K=(kij)m×ni=1,2,…,mj=1,2,…,n

(7)

其中，kij通常采用十分制，是第i个专家给第j个评价指标的评分。

(2)对矩阵K进行标准化处理，得到规范化决策矩阵L=(lij)m×n，如式(8)所示：

(8)

(3)得到主观权重向量W2=(σ1,σ2,σ3,…,σn)T，如下所示：

(9)

式中：λj为评审专家的决策权重。

3.3 计算组合权重

将式(6)和式(9)求得的客观权重和主观权重组合，得到组合权重向量W=(ω1,ω2,ω3,…,ωn)T，计算方法如式(10)所示：

(10)

4 预评分

预评分是通过人的经验，对各年的水资源承载力属性进行打分，这样可以排除个别偏离的数据对最终排名的影响。由于对水资源承载力评价指标的评判不能简单地分为好和不好两种确定的情况，而且仅仅通过最终的排名也不能完全直观的体现水资源承载力的实际情况，因此，本文引用三支决策的评级制思想，在对水资源承载力的评价指标预评分的过程中，根据三支决策的阈值，将水资源承载力的评价指标评为A、B、C三级，并根据最终排名和三支决策的阈值将水资源承载力评为优、良、差三级。

给定水资源承载力评价指标的三支决策阈值α和β，根据下述标准进行评级：对于效益型指标，首先将评价指标值从大到小排序，对于成本型指标，首先将评价指标值从小到大排序，每一个评价指标排名小于等于10α的评定为A，每一个评价指标排名大于10(1-β)的评定为C，其余的评定为B。通过分析各年水资源承载力中A、B、C的个数，得到该年水资源承载力的预评分ψi，评分规则如下：若第i年水资源承载力的评价指标中A占的比重最大，则ψi=1；若第i年水资源承载力的评价指标中B占的比重最大，则ψi=0.5；若第i年水资源承载力的评价指标中C占的比重最大，则ψi=0.1；若第i年水资源承载力的评价指标中A和B一样多且大于C，则ψi=0.75；若第i年水资源承载力的评价指标中A和C一样多且大于B，则ψi0.55；若第i年水资源承载力的评价指标中B和C一样多且大于A，则ψi0.3。

水资源承载力所属类别的评价规则如下：根据水资源承载力的排名，将排名不大于10α的水资源承载力的类别定义为优，将Yi中排名大于10(1-β)的水资源承载力的类别定义为差，其余的水资源承载力的类别定义为良。

5 三支决策-改进TOPSIS方法求排名和类别

TOPSIS方法是多属性决策中经常用到的评价方法，可以判断多个方案的优劣程度。其具体过程如下：

将权重向量W和标准化决策矩阵X相乘，求得加权标准化矩阵Z，如式(11)所示：

Z=(zij)m×n=(ωjxij)m×n

(11)

计算水资源承载力的正理想解初始值Z1负理想解初始值Z0，如式(12)和式(13)所示：

(12)

(13)

计算加权标准化矩阵中的值到正理想解初始值Z1和负理想解初始值Z0关于指标j的灰色关联系数hi(j)以及pi(j)，分别如式(14)和式(15)所示：

(14)

(15)

式中：ρ取0～1范围内的任意值，一般情况下取ρ=0.5。由公式(14)计算不同方案和正理想解初始值Z1的初始灰色关联系数矩阵H，由公式(15)计算不同方案和负理想解初始值Z0的初始灰色关联系数矩阵P，分别如式(16)和式(17)所示：

(16)

(17)

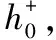
(18)

(19)

(20)

(21)

(22)

(23)

计算不同年份的相对贴进度Ci，如式(24)所示：

(24)

将Ci按大小排序，Ci越大，说明水资源承载力越强，Ci越小，说明水资源承载力越弱。

计算不同年份的最终得分Yi，如式(25)所示：

(25)

式中：ω′为预先给定的Ci在最终得分中占的比重；ω″为预先给定的ψi在最终得分中占的比重，本文中规定，ω′=0.8，ω″=0.2。其中Yi越大，水资源承载力越强。

6 实例分析

本文以文献[12]中的数据为例，选取芜湖市2006-2015年共10年的水资源承载力指标数据，构建水资源承载力指标数据初始数据表，如表2所示。

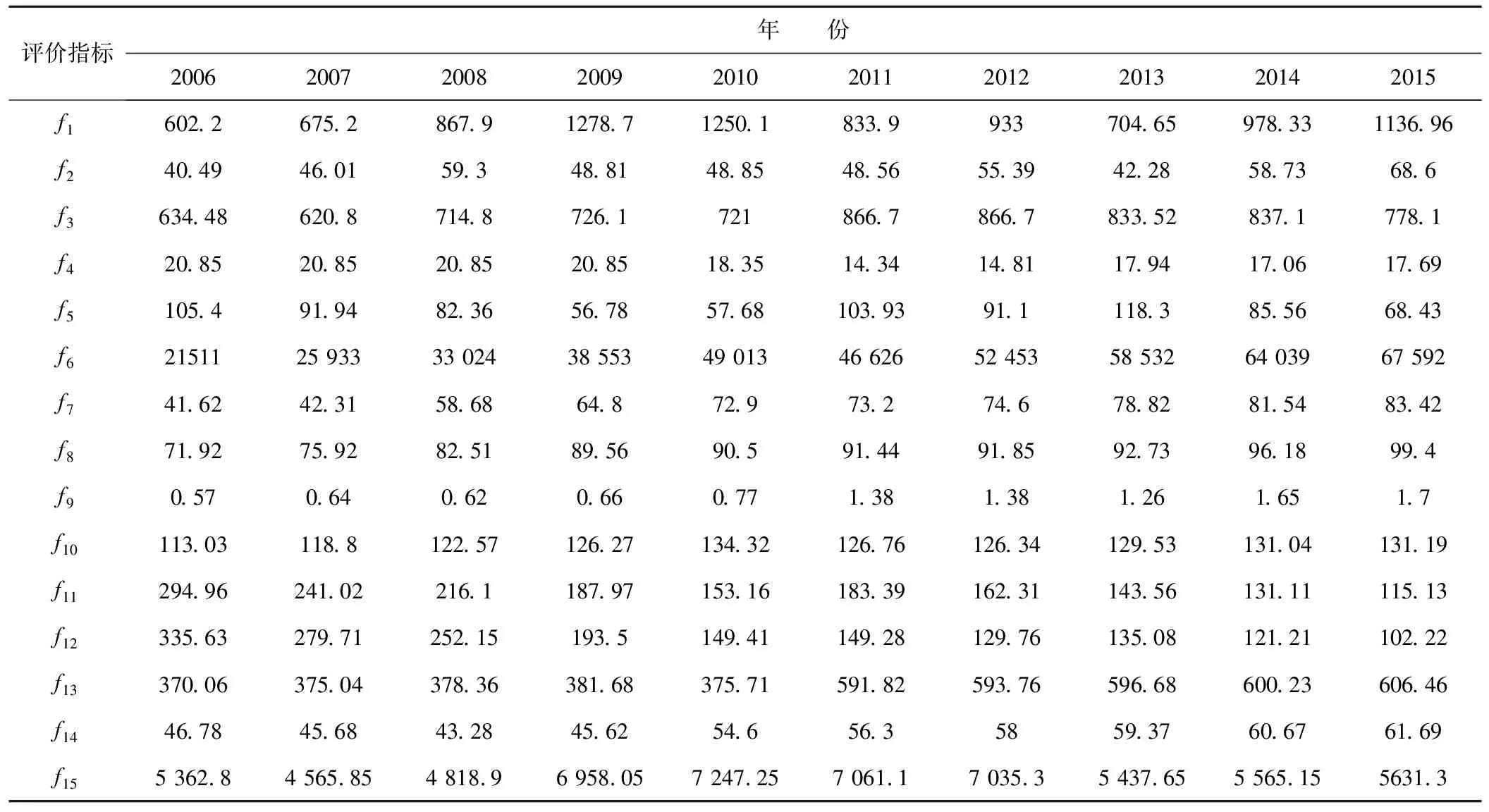
表2 水资源承载力初始数据表

通过公式(1)～(3)，获得标准化决策矩阵X，再通过公式(4)～(6)获得客观权重向量W1，结果如下：

W1=(0.067,0.067,0.069,0.065,0.065,0.065,0.064,

0.063,0.071,0.067,0.062,0.063,0.073,0.069,0.068)T

通过公式(7)～(9)，获得主观权重向量W2，结果如下：

W2=(0.071,0.065,0.076,0.062,0.064,0.070,0.059,0.066,

0.078,0.061,0.048,0.066,0.075,0.071,0.068)T

通过公式(10)获得组合权重向量W，结果如下：

W=(0.071,0.065,0.079,0.060,0.062,0.068,0.057,0.062,

0.083,0.061,0.045,0.062,0.082,0.073,0.069)T

给定三支决策的阈值α=0.2，β=0.3，由于一共10个年份，首先根据评价指标是效益型还是成本型进行排序，不同评价指标中排名不大于2的评级为A，不同评价指标中排名大于7的评级为C，其余的评级为B。按上述标准获得的预评分结果如表3所示。

由公式(25)，求得不同年份水资源承载力的最终得分Yi和排名及类别，结果如表5所示。

表4是只通过改进TOPSIS方法求得的结果，表5是通过三支决策-改进TOPSIS方法求得的结果。从表4可以看出，水资源承载力排名前三的年份分别为2006、2015和2007，排名后三的年份分别为2010、2009和2008；从表5可以看出，水资源承载力排名前三的年份分别为2015、2014和2013，排名后三的

表3 预评分结果

表4 各年份的值及Ci的排名

表5 各年份Yi的值和排名及分类

年份分别为2009、2007和2008。对比表4和表5发现，不同年份水资源承载力的排名有较大差别，通过和文献[12]中的评价结果对比发现，通过三支决策改进TOPSIS方法获得的结果和文献[12]中的结果几乎保持一致，而仅仅通过改进TOPSIS方法获得的结果却不满足文献[12]中的实际情况。通过对比，我们更容易看到三支决策改进TOPSIS方法的优越性和准确性，同时，通过将不同年份的水资源承载力分为优、良、差三级，更便于人们直观地看出不同年份的水资源承载力情况。

7 总 结

本文针对芜湖市2006-2015年十年的水资源承载力数据，提出了一种基于三支决策改进TOPSIS的水资源承载力评价方法，其优越性主要体现在下述三个方面：

(1)通过结合客观权重和主观权重来计算组合权重，使计算结果更加合理；

(2)通过增加预评分来计算水资源承载力的最后得分，能最大程度上排除个别不合理数据的干扰，使水资源承载力的排名更接近实际情况；

(3)通过将不同年份的水资源承载力分为优、良、差三级，便于人们更直观地看出水资源承载力的好坏。