基于PNN网络的水质预测研究

边 冰，赵明政

(华北理工大学，河北 唐山 063210)

0 引 言

水是人类生存和发展的必要资源，同时也是经济发展过程中的命脉[1]。随着我国工业的进程不断发展，水资源匮乏的增长、饮用水和生活水需求的增加，水质、水源和原水的复杂化、分散化和多样化等问题日益加剧，使得传统的生活水生产方面面临着巨大的挑战[2]。2011年，中央一号文件提出我国将要实施更严格的水资源管理制度，对水资源监测提出了更为严厉的准则[3]。水质预测对于水资源的保护及规划起着至关重要的作用。由于水质影响的因素有很多，所以能准确的预测水质成为国内和国外研究的重点。搭建供水安全预警系统和水质监测系统是如今的国家所公认的避免水质污染影响的通用解决供水安全的有效方法。因此做好水质早期预测预报工作是解决饮用水的关键所在。目前用于水质的预测方法有5种，分别为灰色模型预测法、数理统计法、水质模拟模型法、人工神经网络模型预测法和混沌理论预测法等。张青等人[4]将BP人工神经网络方法引入到洪湖水质模型中，结果表明BP神经网络模型具有预测精度较高、预测速度较快的特点。郑鹏等[5]应用改进的BP网络对辽宁河流水质进行了预测，实验结果证明改进的BP网络预测的总氮值精度明显提高。Bobbin[6]等运用遗传算法搭建了基于规则的预测模型，并将其应用到日本的一个湖泊中，初步成果表明该规则可从历史数据水质指标中和环境变量中识别。从而使湖泊水体中藻类变化的原因可从这种规则中得到，并可预测藻类爆发的时间和爆发的范围。本文将针对某水厂2015-2016年两年的数据进行分析处理，然后结合天气情况，通过PNN神经网络对NTU、耗氧量、pH值三个指标进行分类预测，从而采取有效的防御措施来减少损失。

1 PNN神经网络模型理论研究

1.1 PNN网络模型介绍

在1989年，D. F. Specht 博士首先提出PNN神经网络，它是有两个算法发展出的并行算法，这两种算法是贝叶斯分类规则和Parzen窗的概率密度函数估计法[7]。PNN神经网络在解决分类的问题起着重要的作用。PNN网络的优势在于能够在非线性算法等条件下，非线性学习算法所做的工作可以由线性学习算法来完成。

PNN是通过RBF网络发展而来的一种前馈型网络，它的理论依据利用了Bayes决策理论。PNN适用于模式分类，当分布密度SPREAD的值接近0时，构成最邻分类器；当SPREAD的值较大时，它构成对几个训练样本的邻近分类器[8]。

概率神经网络是一种具有良好性能的分类网络，因为它需要考虑样本空间的概率特性，所以隐含层的结点用样本空间中的典型样本来表示，一旦确定就不用再训练，只需根据实际情况进行样本的增减即可，而且概率神经网络具有全局优化的特点[9]。

1.2 概率神经网络的机理

分类器是PNN网络的本质，用概率网络进行分类，确定所属类别Ci的X维向量，如果已知每个类别的概率函数密度fi(X)，就可应用Bayes分类准则，如果下式成立，那么X将被分到Ci类[10]。

PiLifi(X)>PjLjfj(X)

(1)

式中：X属于Ci类的先验概率为Pi，X被错误分类到Ci类的代价为Li。

1.3 概率神经网络的结构

输入层是PNN网络的第一层，它的主要用途是将样本数据传递给下一层，样本记为X=(x1,x2,…,xq)T。

模式层是PNN网络的第二层，该层是由RBF神经元构成。模式层中任何一个神经元的输入都是相同的，并且一般情况下，样本矢量的个数等于模式层神经元的个数。训练样本属于每个类别的概率是输出向量Mij(X)的含义，表达公式为：

i∈{1,2,…,n}，j∈{1,2,…,m}

(2)

式中：所有的模式数由n表示，模式层神经元个数由m表示，第一层与第二层的权值是Wij，δ的含义是平滑因子，并对分类起着关键性的作用。

求和层是PNN网络的第三层。一般的，求和层中的神经元连接的节点是样本相对应类别。第三层只能计算同种类别的输出值之和。其表达式为：

ωij∈[0,1]，i∈{1,2,…,n}

(3)

式中：混合权重由ωij表示，且需要满足的条件是：

(4)

根据(3)可得到最大可能性的输入样本属于Ci类。

输出层是PNN网络的第四层，竞争神经元就是该层的神经元，接受从求和层输出的概率密度函数就是此层的作用，式(1)的功能也是由该层实现的，O(X)代表神经元的输出量。

O(X)=argmax(Si)，i∈{1,2,…,n}

(5)

式(5)的含义为神经元输出为1的是概率密度函数最大的那个，是将要判别样本的模式类别，其余神经元的输出为零。因此得出，概率神经网络将输入量分到最大后验概率的类别中是由贝叶斯分类规则完成的。它具有稳定性好，并且能够容忍一定量的错误样本的特点[11]。概率神经网络基本结构如图1所示。

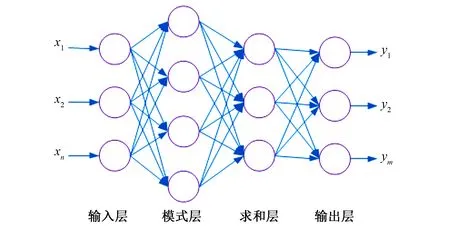
图1 概率神经网络基本结构Fig.1 Basic structure of probabilistic neural network

1.4 PNN网络模型的建立步骤

ANN网络设计步骤流程图如图2所示。

图2 ANN网络设计步骤流程Fig.2 ANN network design procedure

基于MATLAB技术的PNN模型建设过程如下：

(1)随机选取44组样本数据，其中30组作为训练样本，14组作为测试样本。

(2)将水质样本的目标分为3级。

(3)用Train表示训练数据，Test表示测试数据，p_train与t_train分别表示训练数据的输入与输出，p_test与t_test分别表示测试数据的输入与输出。

(4)用ind2vec将期望的类别转化为向量。

(5)使用MATLAB中的newpnn函数建立PNN神经网络，并将SPREAD设定为1。

(6)用Sim函数对训练好的网络进行仿真，然后判别建立的PNN神经网络模型是否符合分类标准，若不符合则调整网络，若符合网络结束。

2 实例应用

2.1 研究区域概括

该水厂的位置处于东部季风区，气候属于暖温带滨海半湿润气候，该市平均降水量约为622.2 mm。全市人均饮用水和生活水的占有量为340 m3，大约占有我国人均水资源的16.7%[12]。

近几年来，随着经济快速的发展，“四点一带”的建设使国家对水资源提出了更高的要求，从而使水资源的供应与需求的矛盾逐渐增加。随着逐年增加的用水和逐年增加的废水、污水，迫使地表水资源环境发生巨大的改变。从而导致水资源越发紧缺，生态环境破坏加剧，出现了一系列水环境污染问题，进而造成了水资源环境的持续恶化[13]。

2.2 数据采集预处理

本文数据资料来源于2015-2016年某水厂的水质监测汇总表。以这两年的监测数据为分析资料，选取表1中3个指标因子，采用PNN网络模型进行水质的预测分类。

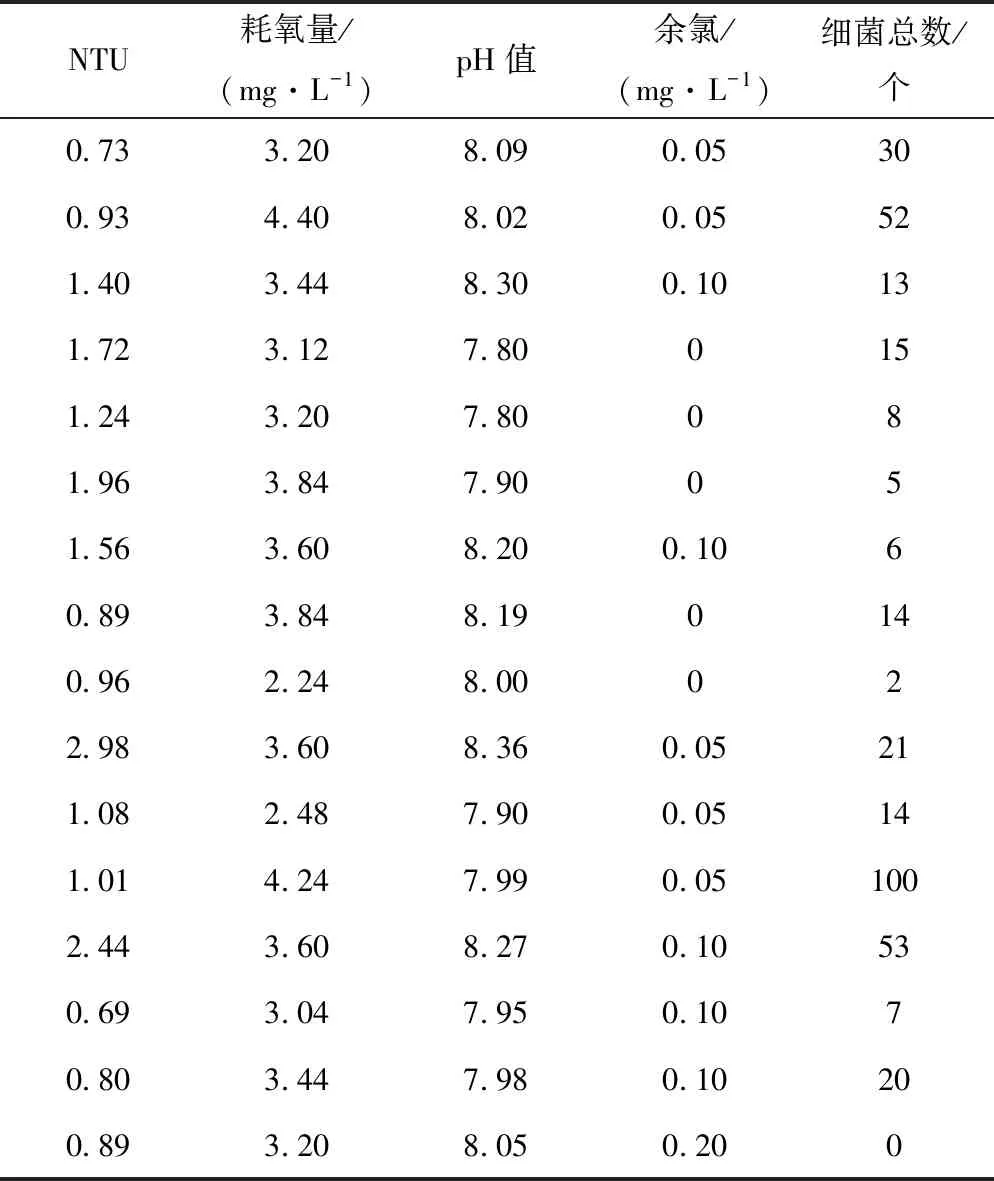
表1 水厂部分指标检测值Tab.1 Detection value of some indicators in waterworks

本文针对水质中NTU、耗氧量和pH值的变化，对水质分成了3个等级分别是1级、2级和3级。其水质等级划定表如表2所示。

由于本文所得数据中pH值均是大于7的偏碱水，所以在1级中pH值没有设置下限。并且每一级中耗氧量、NTU、pH值均必须在表2所对应的范围内，如果其中有一项超标都会被分到下一级去。例如耗氧量为1.20 mg/L，NTU为3.0，pH值为7.8，这组数据的水质将被定为2级。

2.3 输入量的确定

由于本实验是用耗氧量、NTU和pH作为输出量，所以耗氧量、NTU和pH都必须作为输入量。而一年四季有阴晴雨雪，这对NTU这一指标有很大的影响，故而天气变化也必须作为输入量。本实验对水厂数据用MATLAB进行线性拟合来判断输入量与输出量相关度的高低，从而确定其他几个指标是否合适。其拟合图如图3、图4和图5所示。

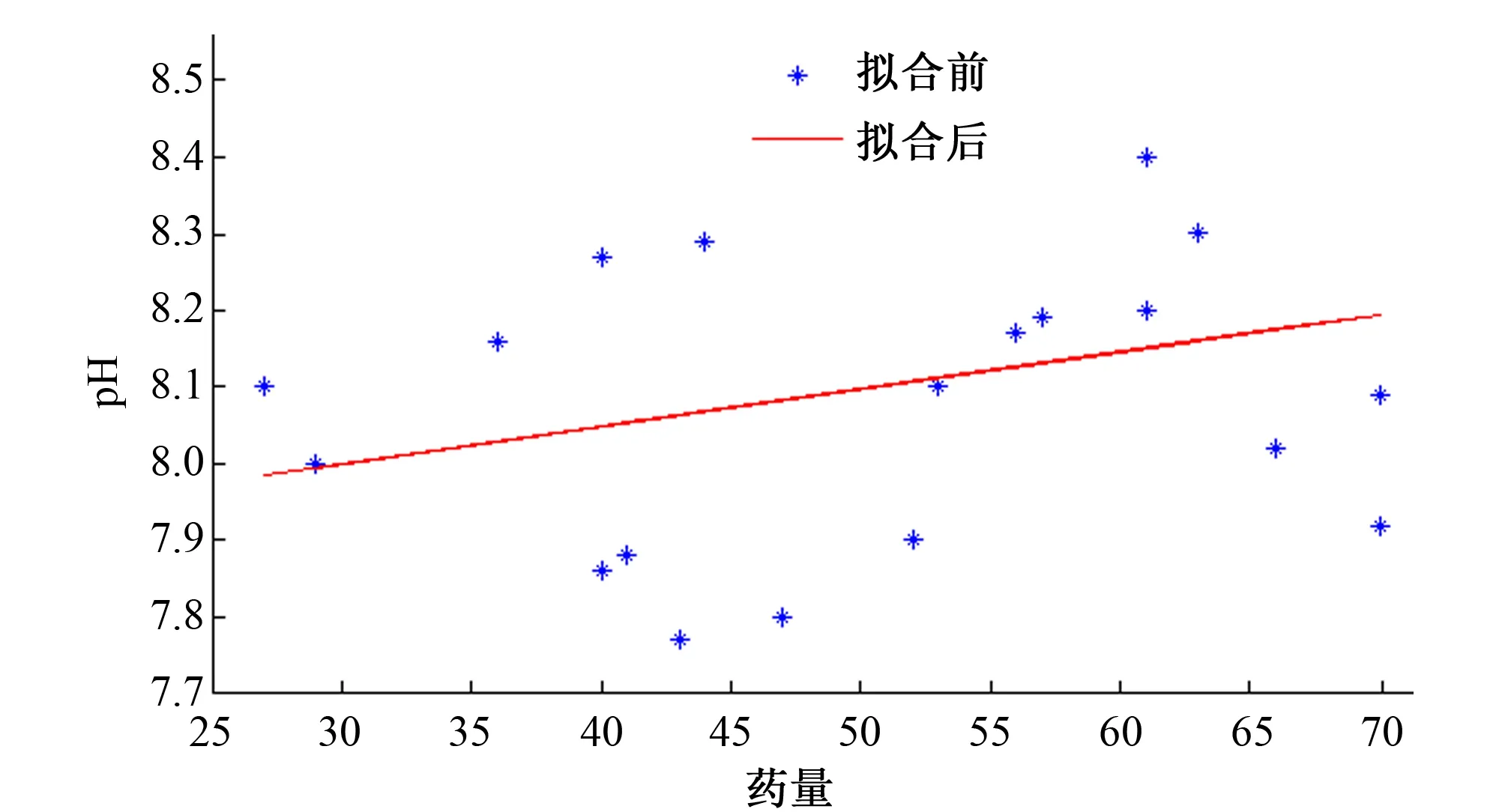
图5 药量与pH的拟合图线Fig.5 Fitting curve of drug volume and pH

根据图3可知，当余氯的浓度增高时，水的pH值会逐渐下降，从而可以判断出余氯与pH值的相关度很高，所以余氯可作为输入量。

根据图4可知，当温度上升时，水的耗氧量会逐渐上升，从而可以判断出温度与耗氧量的相关度很高，所以温度可作为输入量。

根据图5可知，当水中投入的药量增加时，水中的pH值也会随之增加，从而可以判断出药量与pH值的相关度很高，所以药量也可作为输入量。

综上所述，本实验输入量的指标分别是天气、余氯、pH值、温度、药量、NTU和耗氧量。

2.4 仿真与分析对比

该研究共采用了44组数据，训练样本为系统任意抽取的30组，剩余14组作为测试样本。为了能清晰直观的分析对比仿真结果，本实验通过MATLAB仿真，首先给出了基于PNN网络和BP神经网络的误差曲线图。如图6和图7所示。

图6 PNN网络误差曲线图Fig.6 Error curve of PNN network

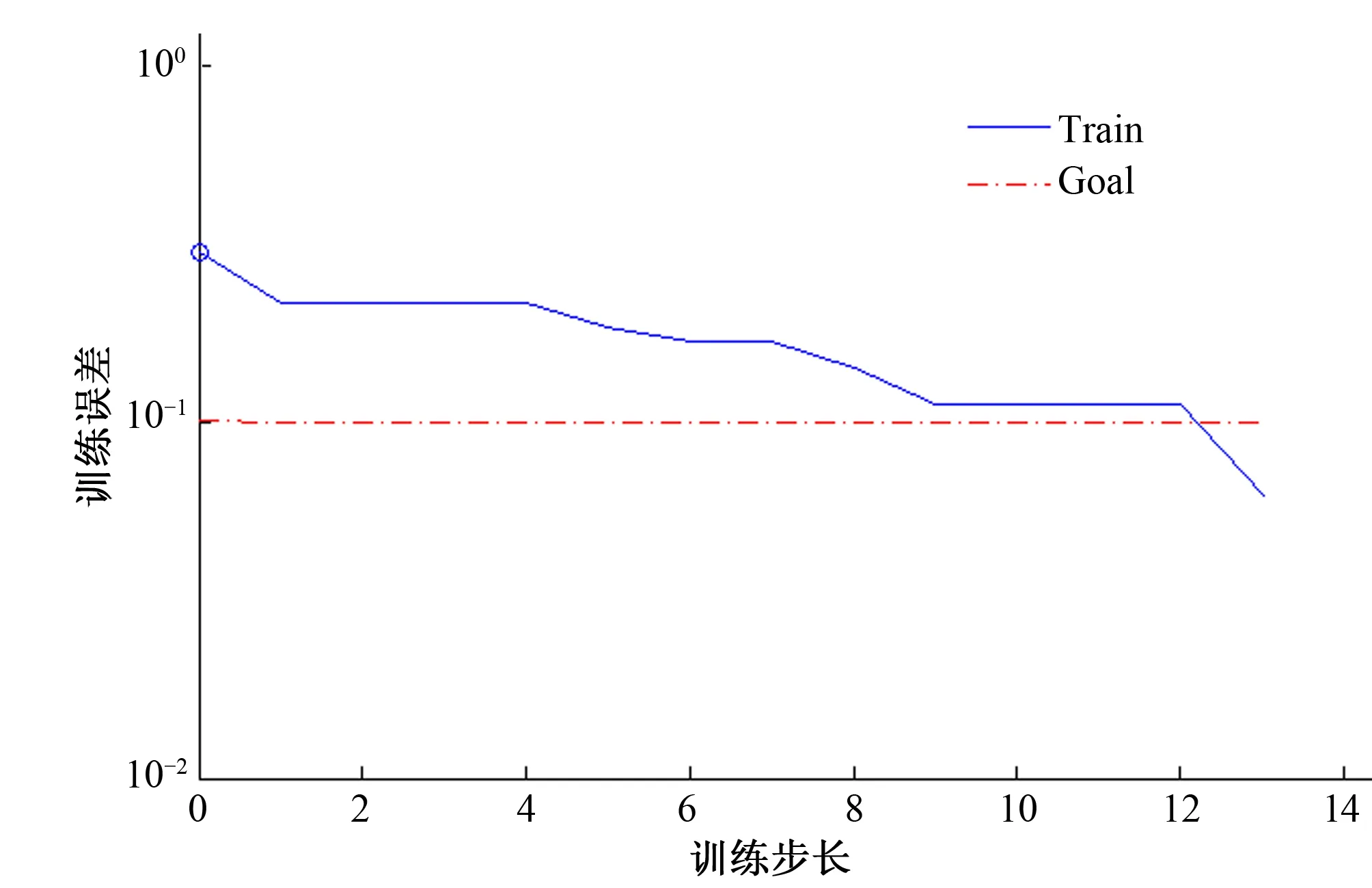
图7 BP网络误差曲线图Fig.7 Error curve of BP network

根据图6和图7的比较可知，PNN网络经过3次训练就可达到误差精度的要求。而BP网络要经过12次训练才可达到误差精度的要求。

为了进一步确定PNN神经网络比BP神经网络的分类预测效果好，最后将训练好的神经网络输入测试组的数据，其结果显示如图8和图9所示。

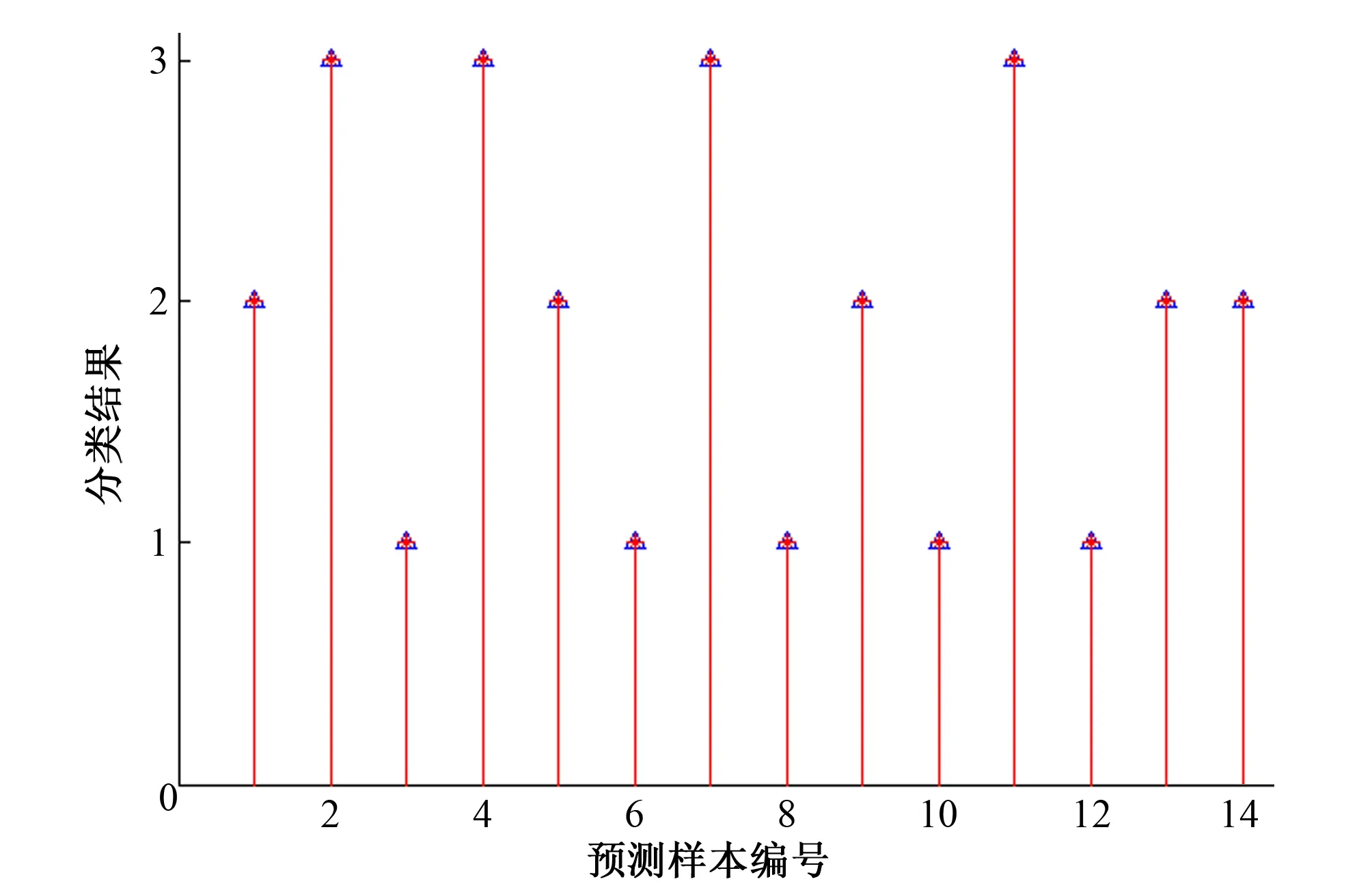
图8 PNN网络预测效果Fig.8 Prediction effect of PNN network

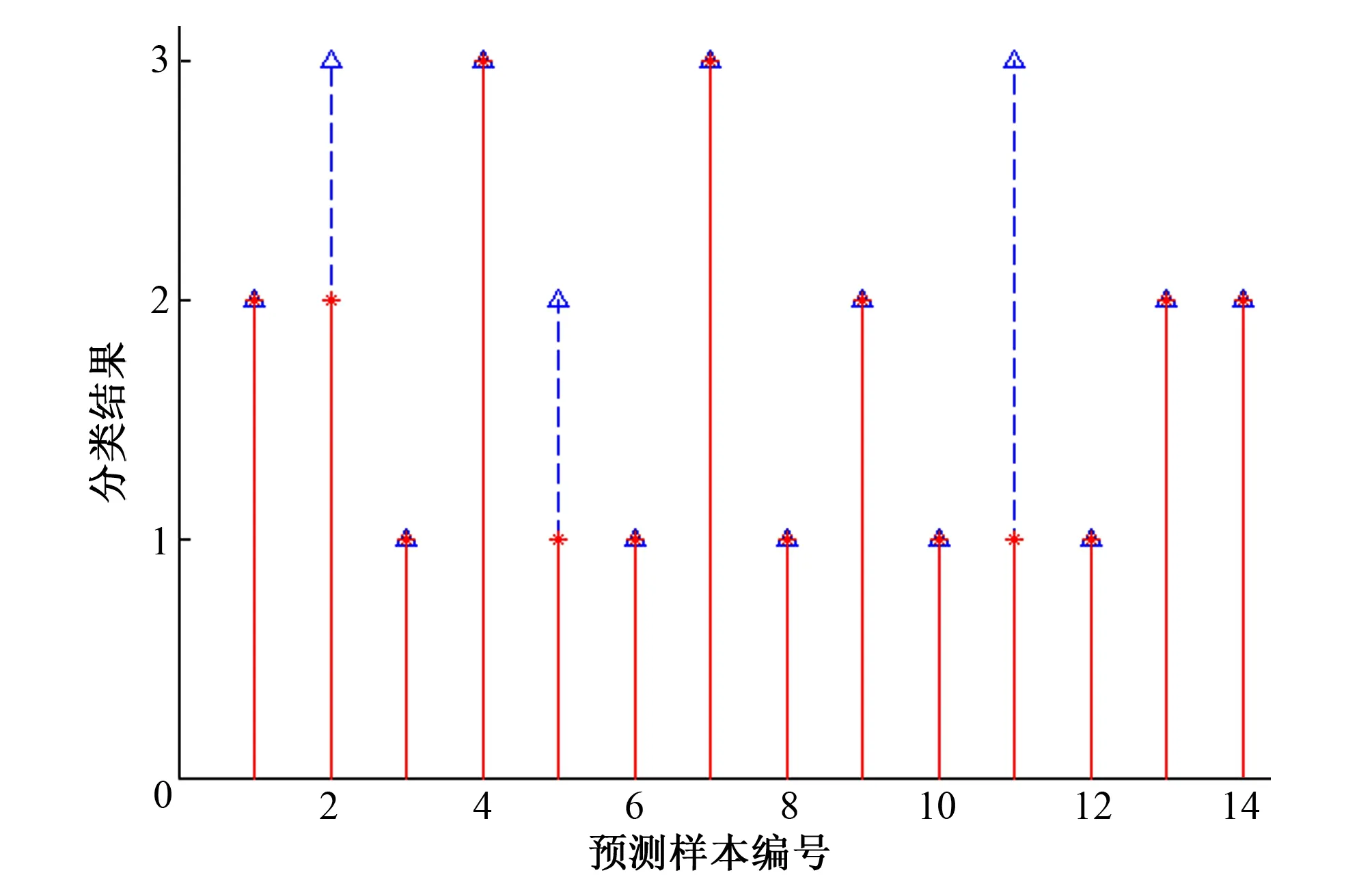
图9 BP网络预测效果Fig.9 Prediction effect of BP network

根据图8和图9可知，PNN预测结果中，预测值和样本值完全一样，而BP预测结果中有3个与样本数据不同。

本实验还通过仿真预测得出了两种网络的预测时长及正确率。如表3所示。

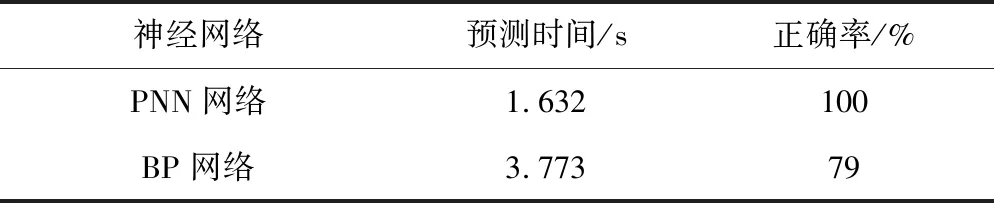
表3 预测时长及正确率Tab.3 Forecast time and accuracy

由表3可知，PNN网络比BP网络预测用时短，并且准确率更高。

3 结 语

(1)经过仿真分析可以看出，采用PNN神经网络模型对自来水水质预测比BP神经网络模型预测，更具有准确性和快速性。

(2)通过两种网络的比较，PNN网络无论在预测时间和正确率上都优于BP网络，从而说明PNN神经网络对水质预测分类方面具有相当高的可信度，并且又给水质预测分类提供了一种简单而又快捷的方法。

□